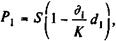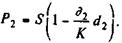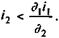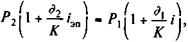Доходность купли продажи депозитных сертификатов

§ 3. Цена и доходность депозитных сертификатов и векселей

По своим основным характеристикам депозитные и сберегательные сертификаты близки к краткосрочным и среднесрочным облигациям. По окончании срока действия сертификата его владелец получает сумму вклада и процентов.

где N — номинал сертификата; D — процентный доход; Rc — процентная ставка по сертификату; Т — срок действия сертификата.

Сумма, выплачиваемая владельцу сертификата при погашении, равна;

Дена сертификата определяется по формуле:

Используя формулу (11.26), получаем:

р [84] So ¦ 10024 ГУ6-

По российскому законодательству депозитные сертификаты предназначены для юридических лиц и выпускаются на срок до одного года. Для физических лиц выпускаются сберегательные сертификаты, срок действия которых может доходить до трех лет. Цена сертификатов, выпускаемых на срок более одного года, определяется так же, как и для облигаций.

Сберегательный сертификат сроком действия 3 года имеет номинал 1000 руб. Проценты выплачиваются раз в полгода. Процентная ставка на первый год — 12% годовых. Требуемая норма прибыли составляет 13% годовых.

На основе анализа состояния финансового рынка инвестор считает, что процентная ставка по сертификатам пересматриваться не будет, и требуемая норма прибыли также останется без изменений. Тогда искомая величина может быть oik ределена по формуле (11.7):

1000 60:[1-О6854] + 685,40 =

= 290,4 + 685,4 = 975,8 руб.

Цена сертификата ниже номинала, так как процентная ставка по сертификату ниже, чем требуемая норма прибыли по данному виду ценных бумаг.

Если известна рыночная цена сертификата и инвестор определил требуемую норму прибыли для данного вида ценных бумаг, то доходность сертификата со сроком погашения меньше года можно определить по формуле (11.18).

Депозитный сертификат номиналом 100 000 руб. выпущен на срок 270 дней. По сертификату установлена процентная ставка из расчета 18% годовых. До погашения сертификата остается 90 дней. Сертификат продается по цене 109 000 руб. Определить доходность сертификата, если покупатель будет держать его до погашения.

Сумма, которую получит инвестор при погашении сертификата, определяется по формуле (11.25) и будет равна:

N+ D = 100 000 ^ + 0483^70 |- 113 315 руб.

Следовательно, доход держателя облигации за период владения (90 дней) составит:

Dn = ИЗ 315- 109 000 = 4315 руб.

Применяя формулу (11.20), получаем:

R ¦= :^31L Х%5Г= 0,1605 или 16,05%.

Общий подход при определении цены дисконтного или процентного векселя остается таким же, как и при определении других краткосрочных ценных бумаг (облигаций или сертификатов). Однако следует иметь в виду, что векселя котируются на основе дисконтной ставки (дисконтной доходности).

Дисконтная доходность определяется по следующей формуле:

где Rj— дисконтная ставка (доходность); D — величина дисконта (процентного дохода) в денежных единицах; N — цена погашения (номинал) векселя; Г—число дней до погашения векселя; 360 —число дней в финансовом году.

Если известна величина дисконта, то цена векселя (Р) будет равна:

Если известна дисконтная ставка, то величину дисконта можно определить из формулы (11.27):

Определить цену векселя номиналом 10 000 руб., до погашения которого остается 45 дней, а дисконтная ставка составляет 10% годовых. Используя формулу (11.29), получаем:

Р = 10000(l-5^-^1=9875 руб.

Дисконтная ставка занижает инвестиционную доходность векселя, так как расчет ведется на базе 360 дней и номинала векселя, тогда как инвестор затрачивает на покупку векселя сумму, которая меньше номинала. Поскольку инвестору приходится сравнивать вложения в покупку векселей с вложениями в другие ценные бумаги, которые котируются на основе 365 дней, то в этом случае цена векселя может быть определена то формуле (11.15).

До погашения векселя номиналом 10 000 руб. остается 45 дней. Дисконтная ставка по векселям составит 10% годовых. Однако инвестор считает, что доходность по векселю с учетом риска должна составить не менее 12%, Определить цену векселя на базе финансового года, равного 365 дням.

Исходя из новых условий, цена векселя на 20 руб. ниже цены, определенной на основе дисконтной ставки.

По процентному векселю держатель при оплате векселя получает номинал векселя и сумму начисленных процентов. Сумма начисленных процентов исчисляется по той же формуле (11.24), как и сумма процентов по депозитному сертификату, только расчет производится на базе финансового года, равного 360 дням:

где D — сумма начисленных процентов в денежных единицах; N — номинал векселя; Ramp; — процентная ставка по векселю; Г — число дней с момента начисления процентов до оплаты векселя.

Соответственно цена процентного векселя определяется по аналогии с ценой сертификата (формула (11.26) на базе финансового года в 360 дней:

где R — требуемая норма прибыли по данному виду ценных бумаг.

Вексель номиналом 100000 руб. предъявлен к оплате через 45 дней со дня начисления процентов. По векселю начисляется 15% годовых. Определить цену векселя, если требуемая норма прибыли составляет 12% годовых.

Применяя формулу (11.31), получаем:

Если известна цена векселя, то его доходность может быть определена по формуле (11.20).

Предлагается дисконтный вексель по цене 9500 руб. Через 90 дней во векселю должна быть выплачена сумма в размере 10 000 руб. Определить дисконтную и инвестиционную доходность векселя.

Дисконтная доходность определяется по формуле (11,27):

10000-9500 360 ; х——1

Используя формулу (11.20), находим инвестиционную доходность.

Источник

Доходность купли-продажи финансовых инструментов

Краткосрочные финансовые инструменты денежно-кредитного рынка — векселя, тратты, различные депозитные сертификаты и т.д. — могут быть проданы до наступления срока их оплаты. Владелец при этом получает некоторый доход, а в неблагоприятных условиях несет убытки.

Покупка и продажа векселя (простая учетная ставка). Если вексель или другой вид долгового обязательства через некоторое время после его покупки и до наступления срока погашения продан, то эффективность этой операции можно измерить в виде простых или сложных процентов. Финансовая результативность операции здесь связана с разностью цен купли-продажи, которые в свою очередь определяются сроками этих актов до погашения векселя и уровнем учетных ставок. Покажем это. Пусть номинал векселяравен S руб. Он был куплен (учтен) по учетной ставке d₁ за 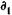дней до наступления срока.

Цена в момент покупки составила

где K — временная база учета.

За 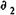дней до погашения вексель был продан с дисконтированием по ставке d₂:

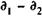
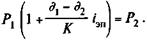
Инвестиции в начале операции составили, таким образом, P₁ руб., отдача от них P₂ руб. Операция продолжалась дней. Наращение вложений за указанный срок по простой или сложной годовой ставке, которую принимают в качестве меры эффективности, должно дать конечный результат, т.е. P₂. Условия операции показаны на рис. 9.4. Для простой ставки i_ЭП получим следующее балансовое уравнение:

(9.7)

Отсюда доходность купли-продажи векселя (в виде ставки простых процентов)

(9.8)

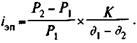
Выразив p₁ и P₂ через определяющие эти величины параметры, находим

(9.9)

Для того чтобы операция не была убыточной, необходимо, чтобы

или P₁

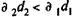
Заменив в формуле (9.11) P₂ и P₁ на адекватные выражения, находим

(9.12)

Очевидно, что реальная доходность (т.е. когда i_Э > 1), как и в случае с простыми процентами, будет иметь место, если 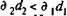или P₁

Обратимся к наиболее распространенному виду сертификата — с разовой выплатой процентов — и рассмотрим три возможных варианта операции купли-продажи этого инструмента по срокам:

а) покупается по номиналу, продается за 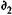дней до погашения;

б) покупается после выпуска и погашается в конце срока;

в) покупается и продается в пределах объявленного срока.

Для варианта а получим знакомое равенство (9.7):

,

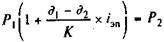
однако символы здесь имеют другое содержание, а именно: Р₁ — номинал, P₂ — цена продажи, 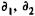— сроки до погашения.

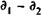
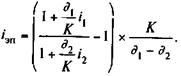
Доходность владения сертификатом в течение дней определяется формулой (9.8), если расчет исходит из цен сертификата. Если же в качестве исходных параметров берутся процентные ставки i₁ и i₂ (i₁ —объявленная ставка сертификата, i₂ —ставка рынка в момент продажи), то

(9.13)

В случае когда измерителем эффективности выступает сложная процентная ставка и заданы цены, получим формулу, аналогичную (9.11). Если расчет основан на уровнях процентных ставок, то

(9.14)

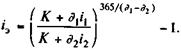
Отметим, что доходность операции имеет место только в том случае, когда 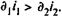Предельное значение i, при котором инвестор получит доход, равно

Перейдем теперь к варианту б. Здесь справедливо равенство

i —объявленная процентная ставка.

Контур для данного уравнения приведен на рис. 9.4. Из приведенного равенства получим значение i_ЭП при заданной величине P₂:

(9.15)

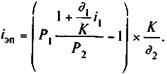
Если в качестве измерителя эффективности принята ставка сложных процентов, то

(9.16)

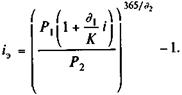
Рассмотрим вариант в. Здесь покупка производится спустя некоторое время после выпуска сертификата, а его продажа — до момента погашения. В этом случае опять приходим к уравнению (9.7), в котором P₁ означает цену приобретения (а не номинал). Отсюда для расчета i_ЭП и i_Э пригодны формулы (9.8) — (9.11).

Как видим, на величины i_ЭП и i_Э в вариантах а, в влияют как срок владения инструментом, так и колебания процентных ставок.

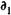
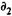
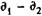
Пример 9.6. Операция заключается в покупке сертификата за 1020 тыс. руб. за 160 дней до его выкупа. Инструмент был продан за 1060 тыс. руб. через 90 дней. Какова доходность операции, измеренная в виде простой и сложной ставок? Исходные данные: Р₁ = 1020, P₂ = 1060, = 160, = 70, = 90.

Пусть временная база простых процентов равна 365 дням, тогда по формуле (9.8) находим

i_ЭП = 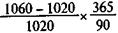= 0,159, т.е. 15,9%. Эквивалентная сложная ставка равна

i_Э = 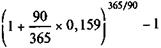= 0,169, т. е. 16,9%.

Величину i_Э можно определить и непосредственно по формуле (9.11):

i_Э = 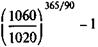= 0,169.

Пример 9.7. Финансовый инструмент, приносящий постоянный процент, куплен за 200 дней до срока его погашения и продан через 100 дней. В момент покупки процентная ставка на рынке была равна 10%, в момент продажи — 9,8%. Доходность операции купли-продажи в виде годовой ставки сложных процентов равна согласно (9.14)

i_Э = = 0,103, т.е. 10,3%.

Пример 9.8. Сертификат с номиналом 100 тыс. руб. с объявленной доходностью 12% годовых (простые проценты) сроком 720 дней куплен за 110 тыс. руб. за 240 дней до его оплаты. Какова доходность инвестиций в виде i_Э?

Если K = 360 дней, то по формуле (9.16) получим

i_Э = 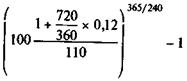= 0,19985, т. е. 19,985%.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник