- Как рассчитать кредит самостоятельно: формула расчёта на калькуляторе
- Как вообще рассчитывается кредит?
- Погашать долг можно по-разному
- Как выглядят формулы расчёта платежей
- Воспользуемся банковскими калькуляторами
- Как это работает
- Пример 1
- Пример 2
- Подумаешь, бином Ньютона!
- Как считать доходность инвестиций: формулы расчета
- Как рассчитать доходность инвестиций?
- Как считать доходность в процентах годовых?
- Как считать среднегодовую доходность
- Как рассчитать среднюю годовую доходность, если известны доходности по годам?
Как рассчитать кредит самостоятельно: формула расчёта на калькуляторе
Как вообще рассчитывается кредит?
Существуют специальные формулы, их несколько, и они взаимосвязаны. Прежде, чем приступить к ним, надо определиться с основными понятиями. Одни интуитивно очевидны, тем более, что задаёте их вы сами:
- сумма займа (СмЗ);
- срок (СрокМ – срок в месяцах), на который даётся кредит.
С годовой процентной ставкой (ПрцСт) тоже более или менее ясно, ведь за предоставление денег придётся платить.
В расчётах применяется как месячная процентная ставка (ПрцСтМес), так и дневная (ПрцСтДн). Они считаются в долях от целого, а не в процентах:
ПрцСтМес = ПрцСт / 12 / 100;
ПрцСтДн = ПрцСт / 365 / 100 или ПрцСт / 366 / 100, если год високосный.
Погашать долг можно по-разному
Видов платежей два. Они бывают аннуитетными или дифференцированными, и от того, какой вы изберёте, зависит картина выплат.
С точки зрения банка, ежемесячный платёж распадается на несколько частей. Главными в них является тело долга и проценты, но есть и прочие составляющие.
Банк в первую очередь заботится о выплатах процентов, поскольку это его доход. Поэтому в первых платежах, какой бы вид вы ни выбрали, основная часть отводится именно им. По мере продвижения к концу срока доля процентной части уменьшается, а доля основного долга, соответственно, увеличивается.
Если платёж аннуитетный, то его величина остаётся постоянной на всём протяжении погашения долга.
Дифференцированный платёж имеет переменный размер, но в нём тоже есть постоянная часть: это доля основного долга. Процентная часть плавающая, она от максимума в первом платеже постепенно уменьшается до нуля в последнем, поскольку рассчитывается от величины оставшейся части долга (ОстДолга).
Для заёмщика выгоднее применять дифференцированные платежи , поскольку в этом случае переплата меньше. Банку, соответственно, интереснее аннуитетные, и в последнее время они решительно преобладают. Делается это, якобы, во благо заёмщика, ведь с постоянным платежом ему удобнее обращаться.
Если срок небольшой и проценты невелики, то и разница некритична. А вот на многолетних ипотеках, да ещё с высокими процентами, расхождение весьма ощутимо.
Как выглядят формулы расчёта платежей
Платёж аннуитетный (ПлАн) одинаков на весь срок выплат, и рассчитывается так:
ПлАн = СмЗ х (ПрцСт / (1 – (1+ ПрцСт) ^ (1-CрокМ)))
Значок «^» означает возведение в степень.
По такой формуле считают обычно в банках, она же заложена в большинство программ для банковских калькуляторов.
Платёж дифференцированный (ПлДф) рассчитывается заново каждый раз, и с каждой выплатой становится всё меньше. Он состоит из двух частей – основного долга (ОснДолг) и Процентов. Посмотрим, как считается каждая часть, а затем сложим их – получим величину ПлДф.
ОснДолг = СмЗ / СрокМ
Проценты = ОстДолга х ПрцСт х (Дней в месяце / Дней в году)
ПлДф = ОснДолг + Проценты
По этим формулам можно только сделать прикидку, в банке могут быть свои схемы расчётов. По-разному рассчитывают кредиты для юридических и физических лиц, для пенсионеров и льготных категорий заёмщиков. Не стоит забывать о страховке, комиссиях и прочем .
Поэтому окончательный вариант сумм и график платежей может составить только сотрудник банка.
Воспользуемся банковскими калькуляторами
Банки побеспокоились о том, чтобы клиенты не морочили себе голову арифметикой, а сразу получали искомые параметры.
Составлено множество программ, которые названы «калькуляторами». Им стоит только задать основные величины, как они тут же произведут расчёт и покажут всё, что интересует заказчика, вплоть до помесячного графика платежей и суммы переплаты за кредит.
Как это работает
Прежде всего надо выбрать вид кредита и банк, с которым вы хотели бы взаимодействовать. Этот выбор чаще всего определяет процентную ставку, или хотя бы диапазон её значений. Далее задаёте сумму займа и срок, на который рассчитываете.
Банковская программа может задать дополнительные вопросы. Например, калькулятор Сбербанка интересуется, не являетесь ли вы его клиентом. Если «да», то вам предоставляют льготу.
Есть калькуляторы, которые предназначены для сравнения условий кредита в разных банках, причём высвечиваются несколько вариантов. Сравнивать удобно, задавая одинаковые исходные данные.
Пример 1
Допустим вы хотите взять кредит в 500 000 руб. на 4 года, и не знаете, какой банк выбрать. На помощь приходит «Универсальный калькулятор», предлагая вам банки на выбор, попарно. Для каждой пары выбираются однотипные кредиты и производится расчёт. Его итоги вам предлагают примерно в таком виде:
| ВТБ Банк Москвы кредит наличными | Сбербанк кредит наличными | |
| Ставка по кредиту | 16.90% | 16% |
| Ежемесячный платеж | 14 402 руб. | 14 170 руб. |
| Общая сумма выплат | 691 296 руб. | 680 167 руб. |
| Переплата в рублях | 191 296 руб. | 180 167 руб. |
| -_» — в процентах | 38,25% | 36.03% |
| Итог: | Переплата меньше на 11 129 руб. по сравнению с другим |
Разница в данном случае родилась из-за того, что процентные ставки для данного типа кредита в банках разные. Вот и выбирайте, где выгоднее.
Пример 2
Также можно сравнить выгоды и недостатки аннуитетного и дифференцированного платежей. Например, вы хотите взять кредит в 1 000 000 руб. на 3 года с процентной ставкой 12% годовых.
Картина получается следующей:
| Аннуитетный | Дифференцированный | |
|---|---|---|
| Ежемесячный платеж | 33 214,31 руб. | от 28 055,56 руб. (это максимум) |
| Общая сумма выплат | 1 195 715,15 руб. | 1 185 000,00 руб. |
| Переплата — в рублях | 195 715,15 руб. | 185 000,00 руб. |
| -_» — в процентах | 19,57% | 18.50% |
| Итог: | Переплата меньше на 10 715 руб. |
Пользуясь калькулятором, можно прогнать разные варианты, тем самым подбирая условия, для вас наиболее выгодные. И только потом, окончательно определившись, можно отправляться в конкретный банк со своими предложениями.
Не факт, что их примут без изменений, но вы уже будете достаточно знакомы с вопросом, чтобы грамотно обсудить предложения банка.
Подумаешь, бином Ньютона!
Наш Андрей, преодолев первоначальную панику, решил попробовать вникнуть в проблему. Куда деваться, кредит всё-таки брать надо!
Он пошёл по более простому пути – использовал различные калькуляторы. Разбираться в формулах пока не рискнул, особенно для аннутиетных платежей. С дифференцированными как раз проблем не возникло, там процесс расчёта логичен и в целом ясен.
Постепенно и потихоньку, с помощью подсказок, благо в интернете полно информации, Андрей начал понимать взаимосвязь параметров. Через пару дней он стал свободно ориентироваться в терминах, видах кредитов, особенностях банков. Так что мог запросто рассчитать стоимость любого потребительского кредита.
Теперь он был готов встретиться с сотрудником банка и проверить своё знание предмета. А заодно и кредит оформить.
Источник
Как считать доходность инвестиций: формулы расчета
Автор: Алексей Мартынов · Опубликовано 01.06.2015 · Обновлено 05.11.2015

Доходность (норма доходности, уровень доходности) — это степень увеличения (или уменьшения) инвестированной суммы за определенный период времени. В отличие от дохода, который выражается в номинальных величинах, то есть в рублях, долларах или евро, доходность выражается в процентах. Доход можно получать в двух видах:
- процентный доход — это проценты по депозитам, купоны по облигациям, дивиденды по акциям, арендная плата по недвижимости;
- рост стоимости купленных активов — когда цена продажи актива больше цены покупки — это акции, облигации, недвижимость, золото, серебро, нефть и другие товарные активы.
Такие активы как недвижимость, акции и облигации могут сочетать в себе два источника дохода. Расчет доходности нужен для оценки роста или падения вложений и является критерием оценки эффективности инвестиций.
Как рассчитать доходность инвестиций?
В общем виде доходность всегда рассчитывается как прибыль (или убыток), деленная на сумму вложенных средств, умноженная на 100%. Прибыль считается как сумма продажи актива — сумма покупки актива + сумма денежных выплат, полученных за период владения активом, то есть процентный доход.
Формула 1
Мы купили акцию по цене 100 рублей (сумма вложений), продали акцию по цене 120 рублей (сумма продажи), за период владения акцией получили 5 рублей дивидендов (денежные выплаты). Считаем доходность: (120-100+5)/100 = 0,25 ∗ 100% = 25%.
Формула 2
Есть вторая формула, по которой доходность считается как сумма продажи актива + сумма денежных выплат, деленная на сумму вложений, минус 1, умноженная на 100%.
Как считать доходность в процентах годовых?
В формуле расчета простой доходности не учитывается такой важный параметр, как время. 25% можно получить за месяц, а можно и за 5 лет. Как тогда корректно сравнить доходность активов, время владения которыми различается? Для этого считают доходность в процентах годовых. Доходность в процентах годовых рассчитывается для того, чтобы сравнить друг с другом эффективность активов, время владения которыми отличается. Доходность в процентах годовых — это доходность, приведенная к единому знаменателю — доходности за год.
К примеру банковский вклад дает 11% в год, а какие-то акции принесли 15% за 1,5 года владения ими, что было выгоднее? На первый взгляд акции, они ведь принесли доходность больше. Но инвестор владел ими больше на полгода, поэтому их доходность как бы растянута во времени по сравнению с депозитом. Поэтому, чтобы корректно сравнить депозит и акции, доходность акций нужно пересчитать в процентах годовых.
Для этого в формулу добавляется коэффициент 365/T, где Т — количество дней владения активом.
Мы купили акцию за 100 рублей, продали через 1,5 года за 115 рублей. 1,5 года это 1,5*365=547 дней.
(115-100)/100 ∗ 365/547 ∗ 100% = 10%. В этом случае депозит оказался немного выгоднее акций.
Как форекс, управляющие компании, брокеры и банки манипулируют годовой доходностью.
В любой рекламе доходности обращайте внимание на сноски, уточняйте какую доходность указывают в рекламе и за какой период. К примеру, в рекламе звучит доходность 48% годовых. Но она может быть получена всего лишь за один месяц. То есть компания за месяц заработала 4% и теперь с гордостью рекламирует продукт, дающий 4*12=48% годовых. Даже вы, заработав за день на бирже 1%, можете хвастаться, что заработали 365% годовых) Только доходность эта виртуальная.
 Как считать среднегодовую доходность
Как считать среднегодовую доходность
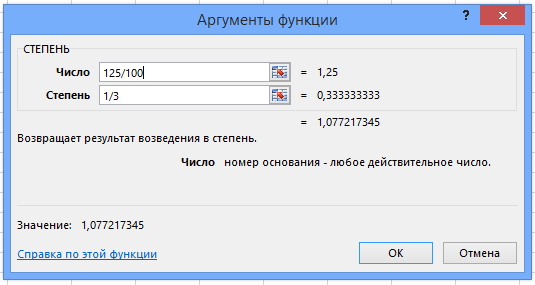
Срок владения активами может составлять несколько лет. При этом большинство активов не растет на одну и ту же величину. Такие активы как акции могут падать или расти на десятки или сотни процентов в год. Поэтому хочется знать, сколько в среднем в год росли ваши инвестиции. Как тогда вычислить среднюю годовую доходность? Среднегодовая доходность рассчитывается через извлечение корня по формуле:
Формула 1
где n — количество лет владения активом.
3√125/100 — 1 ∗ 100% = 7,72%
Формула 2
Другая формула расчета среднегодовой доходности — через возведение в степень.

Как рассчитать среднюю годовую доходность, если известны доходности по годам?
Если известны доходности актива по годам, то среднюю годовую доходность можно вычислить перемножив годовые доходности и извлечь из произведения корень в степени равной количеству лет.
Для начала переведите доходности из процентов в числа.
Эти формулы учитывают эффект сложных процентов. Простая формула расчета доходности этого не учитывает и завышает доходность, что не совсем правильно.
Источник






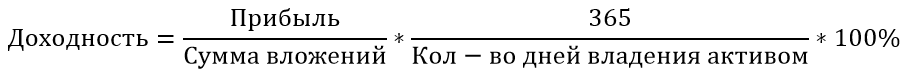
 Как считать среднегодовую доходность
Как считать среднегодовую доходность