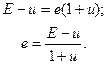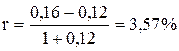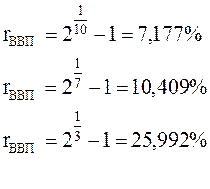- Решение. Используя формулу И. Фишера, можно получить формулу нахождения реальной нормы доходности
- Доходность инвестиций составляет 12 инфляция 15
- Анализ инвестиционной деятельности предприятия
- Оценка влияния инфляции на принятие долгосрочных инвестиционных решений
- Ставка процента, учитывающая инфляцию. Формула Фишера.
Решение. Используя формулу И. Фишера, можно получить формулу нахождения реальной нормы доходности



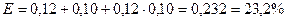
Используя формулу И. Фишера, можно получить формулу нахождения реальной нормы доходности
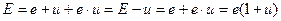
Пример
Какой реальный уровень доходности обеспечит себе инвестор, если прогнозируемый уровень инфляции – 12% в год, а объявленная доходность 16%?
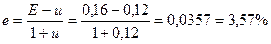
Таким образом, при определении интегральных показателей эффективности инвестиционного проекта в качестве нормы дисконта может использоваться как номинальная, так и реальная норма дисконта. Выбор зависит от характера денежного потока. Если денежный поток представлен в базовых и дефлированных ценах, то следует использовать реальную норму дисконта. Если денежный поток представлен в прогнозном уровне цен, то следует использовать номинальную норму дисконта.
4.5. Анализ финансового состояния предприятия –
участника проекта
Необходимость анализа финансового состояния в инвестиционном проектировании возникает при оформлении кредитной заявки в банк. Предприятие-заемщик должно подтвердить свое платежеспособное состояние. Кроме того, оценка эффективности инвестиционного проекта должна быть дополнена расчетами по влиянию реализации проекта на основные финансовые показатели предприятия – участника проекта.
В соответствии с Методикой оценки инвестиционных проектов [19] для решения поставленной задачи используются четыре группы показателей:
1. Коэффициенты ликвидности, которые характеризуют способность предприятия погашать свои краткосрочные обязательства:
— коэффициент текущей ликвидности;
— коэффициент быстрой ликвидности;
— коэффициент абсолютной ликвидности.
Методика расчета коэффициентов ликвидности детально изложена в разделе 3.5 учебника.
2. Показатели платежеспособности и финансовой устойчивости, используемые для оценки способности предприятия выполнять свои долгосрочные обязательства:
– коэффициент соотношения заемных и собственных средств;
– коэффициент долгосрочного привлечения заемных средств;
– коэффициент покрытия долгосрочных обязательств.
Методика расчета коэффициента соотношения заемных и собственных средств приведена в разделе 3.6 учебника.
Коэффициент долгосрочного привлечения заемных средств ( 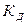
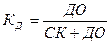
где 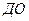
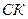
Коэффициент покрытия долгосрочных обязательств ( 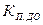
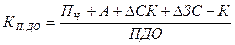
где ПЧ – прибыль чистая; А – амортизация; DСК – прирост собственного капитала в течение года; DЗС – прирост заемных средств в течение года; К – сумма осуществленных в отчетном году инвестиций; ПДО – платежи по долгосрочным обязательствам (погашение займов и выплата процентов по ним).
3. Коэффициенты оборачиваемости, применяются для оценки эффективности операционной деятельности:
– коэффициент оборачиваемости капитала;
– коэффициент оборачиваемости собственного капитала;
– коэффициент оборачиваемости запасов;
– коэффициент оборачиваемости дебиторской задолженности;
– средний срок оборота кредиторской задолженности.
Методика расчета коэффициентов оборачиваемости детально изложена в разделе 3.9 учебника.
4. Показатели рентабельности,применяются для оценки текущей прибыльности предприятия – участника проекта:
– рентабельность продаж по прибыли до налогообложения и по чистой прибыли;
– рентабельность активов (капитала) по прибыли до налогообложения и по чистой прибыли;
– рентабельность собственного капитала.
Методика расчета показателей рентабельности детально изложена в разделе 3.8 учебника.
Указанный перечень показателей может быть дополнен по требованию отдельных участников проекта и финансовых структур.
Показатели анализируются в динамике и сопоставляются с показателями аналогичных предприятий.
Методика более полного анализа финансового состояния предприятия приведена в 3 разделе данного учебника.
Источник
Доходность инвестиций составляет 12 инфляция 15
Анализ инвестиционной деятельности предприятия
Оценка влияния инфляции на принятие долгосрочных инвестиционных решений
При принятии долгосрочных инвестиционных решений необходимо учитывать влияние инфляции. Игнорирование фактора инфляции может негативно отразиться на конечных результатах анализа эффективности долгосрочных инвестиций, привести к неправильным выводам о целесообразности принятия инвестиционных проектов.
При анализе инвестиционных проектов необходимо учитывать инфляционную ставку за каждый анализируемый период инвестирования, а также за весь срок реализации проекта. Особое внимание следует уделять динамике изменения цен на основные ресурсы (сырье и материалы, оборудование, и т.д.), процентные ставки по депозитам и кредитам, уровню доходности инвестиций. Для этого необходимо учитывать основные тенденции цен на основные виды ресурсов при разработке потребности в денежных средствах для покрытия затрат. Например, предприятию для осуществления инвестиционного проекта необходимо использовать три вида сырья: «А», «В» и «С». Доля каждого соответственно 30%, 50% и 20%. Цена на усл. ед. сырья «А», «В» и «С» в предыдущий период была соответственно 180 руб., 420 руб. и 800 руб., в отчетный период соответственно составила 190 руб., 445 руб. и 920 руб. Тогда в среднем индекс роста цен по данным видам сырья для предприятия составил:
Jцс = (190 : 180) * 0,30 + (445 : 420) * 0,50 + (920 : 800) * 0,20 = 1,06 * 0,30 + 1,06 * 0,50 + 1,15 * 0,20 = 0,32 + 0,53 + 0,23 = 1,08.
В отчетный период цена на сырье «А» увеличилась на 6%, цена на сырье «В» увеличилось также на 6%, а цена на сырье «С» на 15%. С учетом структуры материальных ресурсов индекс роста цен на сырье и материалы для предприятия составил 8%. Таким образом, покупательная способность денежных средств предприятия в отчетный период снизилась на 92,59% (1 : 1,08 = 0,925926), следовательно, инфляционная составляющая по материальным ресурсам составила 7,41% (100 — 92,59). Если материальные расходы за период составляют 1000 тыс. руб., то необходимо предусмотреть денежных средств в размере 1074,1 тыс. руб.
Учитывая динамику изменения уровней инфляции, необходимо рассчитывать среднюю ставку по инфляции с использованием формулы средней геометрической:
I1, I2, …, Ik — соответственно ставка инфляции в первый, второй, к-й год реализации инвестиционного проекта;
K — расчетный период проекта.
Например, за прошедшие 5 полугодий до инвестирования индекс роста инфляции составлял 1,05, 1,08, 1,06, 1,07, 1,09, тогда средняя ставка по инфляции составила:
Ic =[1,05 * 1,08 * 1,06 * 1,07 * 1,09] 1 : 5 — 1 = 1,0699 — 1 = 0,0699, или 6,99%.
То есть в среднем каждое полугодие инфляция увеличилась на 6,99%.
Очевидно, что норма отдачи от инвестиций должна быть такой, чтобы прогнозируемый чистый доход от инвестиций не был отрицательным. Поэтому при рассмотрении отдачи от инвестиционных решений необходимо учитывать не только минимальную ставку доходности от инвестиций (СТдм), но и соответствующую реальную ставку инфляции для предприятия (СТин). Это позволит объективно подходить к расчету реальной ставки доходности (СТреа), норме рентабельности от инвестиций. Расчет такой ставки осуществляем по формуле:
СТреа = (1 + СТдм) * (1 + СТин) — 1.
Соответственно норма рентабельности на вложенные средства R должна быть не менее реальной ставки доходности:
Например, если средний уровень инфляции для предприятия составил 6,99%, минимальная норма доходности от вложения средств в развитие производственной базы 12%, то реальная ставка доходности для предприятия будет равна:
СТреа = (1 + СТдм) * (1 + СТин) — 1 = (1 + 0,0699) * (1 + 0,12) — 1 = 0,1983, или 19,83%.
То есть, чтобы получить на каждый вложенный рубль в развитие производственной базы 12 коп., защищенной от инфляции необходимо установить номинальную ставку дохода в 19,83%.
Тогда рентабельность от инвестиций должна быть не менее 20%.
Если известна величина чистого денежного потока (ТД), которая регулярно будет поступать на протяжении установленного срока инвестиционного проекта Т, заданная норма рентабельности на вложенные средства (R), то для оценки будущей стоимости одной денежной единицы в конце срока реализации инвестиционного проекта рассчитывают показатель — множитель текущей стоимости по формуле:
Ставка процента, учитывающая инфляцию. Формула Фишера.
Пусть rn – ставка процента, учитывающая инфляцию (номинальная ставка процента), r — реальная ставка банковского процента (реальная процентная ставка), i ставка темпа инфляции.
Пусть S(0) — капитал в начале года. Тогда, капитал в конце года с одной стороны должен быть равен:
С другой стороны он равен:
S(1) = (1+i) (1+r) S(0).
Приравнивая капиталы в конце года, вычисленные по разным формулам, получим формула Фишера, связывающую номинальную rn и реальная r ставка процента с темпом инфляции i:
rn = r + i + i r (2.25)
Величина i r– называетсяинфляционной премией.
Банк начисляет проценты по номинальной ставке 16 %. Уровень инфляции составляет 12 %. Определить реальную ставку банковского процента с учетом инфляционной премии.
Из формулы Фишера вычисляем реальную процентную ставку r через номинальную ставку процента rn и темп инфляции i:
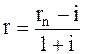
В нашем случае получим:
Таким образом, при большой инфляции реальная ставка банковского процента, равная 3,57 %, меньше разности между номинальной ставкой и инфляцией 16 % — 12% = 4 %.
Первоначальный капитал в размере 200 тыс. руб. выдается на три года, проценты начисляются в конце каждого квартала по номинальной ставке 8 %. Уровень инфляции составляет 12 %.
Определить наращенную сумму с учетом и без учета инфляционной премии.
Наращенная сумма без учета инфляции из (2.11) равна:
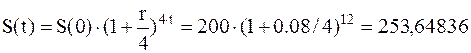
Наращенная сумма с учетом инфляции может быть вычислена по формуле сложных процентов (2.10):

В связи с тем, что уровень инфляции больше чем номинальная процентная ставка, наращенная сумма с учетом инфляции меньше первоначального капитала.
Имеется вексель следующей формы:
«20000 руб. Санкт-Петербург. 1 сентября 2010 г. Обязуюсь уплатить через 60 дней после данной даты по распоряжению гражданина А 20000 руб. с процентной ставкой 11 % годовых.
/подпись/ гражданин В».
За сколько банк купит вексель 1 октября 2010 г., если банковская процентная ставка 9,5 %?
Сумма, которую должен получить гражданин А через 60 дней вычисляется по схеме простых процентов и равна 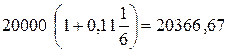
Отсюда получается уравнение: 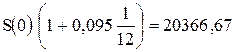
где S(0) – сумма, которую уплатит банк за вексель.
Окончательно S(0)=20206,70 руб.
В течение первого месяца цена товара увеличилась на 30 %, а в течение следующего месяца новая цена товара уменьшилась на 10 %. На сколько процентов изменилась цена товара за 2 месяца?
Эффективная ставка
Формула сложных процентов (2.10) включает четыре неизвестных S(0), S(t), r, t. Зная три неизвестных из уравнения (2.10) можно определить четвертое неизвестное. Сама формула сложных процентов (2.10) определяет будущий капитал S(t) через настоящий капитал S(0), процентную ставку r и время t.
В примере 11 находится время t накопления капитала при известных значениях настоящего S(0) и будущего капитала S(t) и процентной ставки r. В предыдущем разделе, посвященном дисконтированию, в формуле (2.23) современное значение S(0) капитала определяется по его будущему значению S(t), процентной ставке r и времени t. Из формулы сложных процентов (2.10) не определялась только процентная ставка r через настоящий S(0) и будущий S(t) капитал и время t. Решение этой задачи связано с очень важным экономическим понятием эффективной ставки.
Для сравнения различных вариантов сделок удобно использовать эффективную ставку 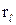
Эффективной называют годичную ставку 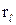
Из (2.10) имеем уравнение для определения 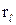
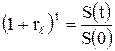
где t – длительность сделки в годах.

Очевидно, что эффективная ставка не зависит от объемов конкретных сумм S(0) и S(t), а определяется только отношениями этих сумм.
Найти эффективную ставку сделки, в результате которой первоначальный капитал утроился за 5 лет.
Согласно (2.26) имеем 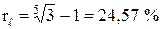
Пример 22. Удвоение ВВП.
Найти ежегодный темп роста ВВП, при котором он удвоится за 10 лет, за 7 лет, за 3 года.
Воспользовавшись формулой эффективной ставки (2.26):
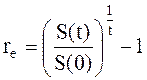
получим ежегодный темп роста ВВП, соответственно, для 10 лет, 7 лет и
В долг дана сумма 2 млн руб. с условием возврата через 2,5 года 3 млн руб. Тогда эффективная ставка в данный сделке равна:
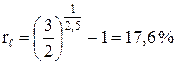
Выдан кредит в 2 млн руб. на 3 месяца под 100 % годовых. Найти эффективную ставку.
Учитывая, что кредит краткосрочный, сумма, выплачиваемая через 3 месяца, будет равна:

тогда эффективная ставка будет равна:

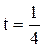

Вексель выдан на сумму 50 млн руб. и содержит обязательство выплатить владельцу эту сумму через 4 месяца. Владелец предъявил банку вексель досрочно. Банк согласился учесть вексель, но с дисконтом 24 % годовых. Найти эффективную ставку.
Полученная сумма будет равна:

Тогда эффективная ставка будет равна:

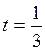
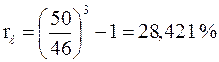
Вексель 3 млн руб. выдан на 2 года с годовой учетной ставкой 10 % с дисконтированием 2 раза в год. Найти эффективную ставку. По формуле (2.24) найдем исходную сумму, выплаченную по векселю:
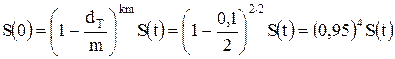
Тогда 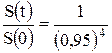

Остров Манхеттен был продан в 1624 г. за $24. В 1976 г. его стоимость была $40×10 9 . Какова эффективная ставка сделки?
В данной задаче интуиция обманывает человека: кажется, что эффективная процентная ставка будет очень большой. Однако расчет по формуле (2.26) даёт следующее значение:
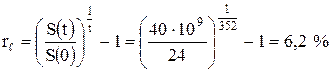
Решающим фактором, приводящим к столь скромному значению эффективной процентной ставки, является время. Длительность сделки велика ‑ 352 года.
В ряде случаев для сравнения различных вариантов сделок вместо эффективной ставки 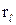
Процентной спот-ставкой называют годичную ставку rs непрерывных процентов, обеспечивающую заданное отношение полученной суммы S(t) к выданной сумме S(0), независимо от того, какая схема оплат используется в данной конкретной сделке.
Из (2.12) имеем уравнение для определения rs:
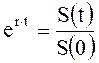
где t – длительность сделки в годах.
Тогда, после логарифмирования имеем:
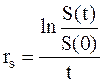
Очевидно, что спот-ставка не зависит от объемов конкретных сумм S(0) и S(t), а определяется только отношениями этих сумм.
Спот-ставка всегда меньше эффективной ставки сделки.
Для примеров 21-27 найти спот-ставки rs.
Пример 21. rs = 
Пример 22. rs = 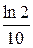

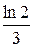
Пример 23. rs = 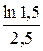
Пример 24. rs = 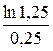
Пример 25. rs =3 ln 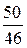
Источник