Доходность финансового актива как это называется

Понятие доходности финансового актива

Одним из ключевых показателей, используемых при оценке целесообразности инвестиций в тот или иной вид актива, является доходность финансового актива. В общем случае это относительный показатель, рассчитываемый как отношение абсолютной величины дохода, генерируемого данным активом, и величины инвестиции в этот актив.

(6.3)

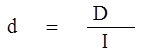
где D – абсолютная величина дохода по активу;

I – величина инвестиции в актив.

В зависимости от вида финансового актива в качестве дохода D чаще всего выступают дивиденд, процент, прирост капитализированной стоимости. Таким образом, существуют различные варианты расчета доходности. Этот показатель измеряется в процентах или долях единицы.

В анализе речь может идти о двух видах доходности – фактичес­кой и ожидаемой. Первая рассчитывается post factum и имеет значе­ние лишь для ретроспективного анализа. Гораздо больший интерес представляет ожидаемая доходность, которая рассчитывается на об­нове прогнозных данных в рамках имитационного перспективного анализа и используется для принятия решения о целесообразности приобретения тех или иных финансовых активов. Логика расчета показателей доходности может быть описана сле­дующим образом.

Приобретая некий финансовый актив, например акции, инвестор вправе рассчитывать на два вида потенциальных доходов: а) диви­денд; б) доход от прироста капитала. Очевидно, что оба поступления не являются безусловньми и могут состояться, как правило, в случае эффективной работы компании, чьи акции приобретены. Оговорка «как правило» сделана потому, что, например, динамика дивидендов и прибыли совершенно не обязаны совпадать. Так, многие компании в экономически развитых странах нередко считают целесообразным выплатить дивиденды даже в том случае, если отчетный год закончен с убытком. Причина такой на первый взгляд нелогичной политики зак­лючается в том, чтобы избежать нежелательных последствий сиг­нального эффекта негативной информации.

В отношении доходности считается, что цена финансового актива, приобретенного (или возможного к приобретению по желанию инвестора) в некоторый момент времени t₀, когда и проводится анализ, определенно известна и равна Р₀. Известен и регулярный доход D₀ в виде процентов или дивидендов, полученных за период, истекший в момент времени t₀. Ожидается, что за следую­щий период t₁ регулярный доход составит величину D₁ и по исте­чении данного периода актив может быть реализован по цене P₁ (ожи­даемая величина). Величина (P₁ – Р₀) представляет собой доход от прироста капитала (или доход от капитализации).

Итак, в данной схеме в отношении D₀ и Р₀ известны их фактические значе­ния, D₁ представляет собой исходную прогнозную оценку, а Р₁ явля­ется целевым расчетньм показателем. Обычно считается, что Р₁ > Р₀, хотя в принципе выполнение этого неравенства не является обязатель­ным, и в этом случае говорят об убытке от капитализации и соответ­ствующей ему отрицательной доходности.

Таким образом, общий до­ход, генерируемый инвестицией Р₀, за данный период t₁ соста­вит величину D₁ + (P₁ – P₀), а общая доходность d будет равна:

(6.4)

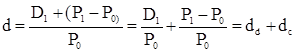
Первое слагаемое d_d в формуле (4) представляет собой текущую доходность (в приложении к акциям она называется также диви­дендной), второе слагаемое d_c носит название капитализированная доходность. Из приведенной формулы хорошо видно, что общий до­ход (или, что в данном случае равносильно, общая доходность) имеет два компонента, причем в зависимости от успешности работы и стра­тегии развития компании, эмитировавшей данный актив, весомость того или иного компонента может быть различной. Таким образом, выбирая для покупки акции той или иной компании, инвестор должен расставить для себя приоритеты – что важнее, дивиденды или доход от прироста капитала.

Формула (4) дает простейший алгоритм расчета доходности, однако возможен и другой подход в рамках фундаменталистской теории. Логика рассуждений в этом случае такова.

Если предположить, что рынок ценных бумаг является эффективным и находится в состоянии равновесия, то в отношении конкретного финансового актива в любой момент времени известны его текущая цена и доходы, которые, как ожидается, этот актив будет генерировать в будущем. Зная эти оценки, можно вычислить параметр r формулы (1), полученное значение которого и можно трактовать как общую доходность данного актива.

(6.5)

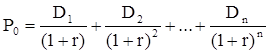
Значение Р₀ представляет собой оценку текущей внутренней сто­имости финансового актива и в условиях эффективного и равновес­ного рынка совпадает с его текущей рыночной ценой на начало пери­ода t₀. Если делать оценку актива с пози­ции конца периода t₁, то исходный поток ожидаемых поступлений связан с текущей ценой актива следующей формулой:

(6.6)

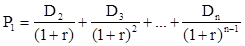
Таким образом, формула (5) преобразуется следующим образом:

(6.7)

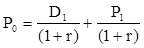
Отметим, что смысл знаменателя второго слагаемого в формуле (7) зак­лючается в дисконтировании P₁, т.е. приведении ее к моменту време­ни t₀. Разрешая это уравнение относительно r, и обозначая его через d, как раз и получим формулу (4).

Следует обратить внимание, что в зависимости от вида финансового актива и абсолютных показателей, выбранных для его характеристики, мож­но исчислить несколько числовых характеристик доходности. Посколь­ку их значения могут существенно различаться, нельзя говорить о не­кой абстрактной доходности, необходимо обязательно уточнять, о чем идет речь, какой алгоритм используется для расчета. В данной лекции мы не будем рассматривать формулы расчета для конкретных финансовых инструментов, поскольку это было сделано в более ранних курсах.

Источник

Доходность финансового актива

Доходность финансового актива — это относительный показа­тель, характеризующий эффективность использования финансовых активов. Показатели доходности используются для обоснования ре­шений о целесообразности приобретения акций и облигаций.

Исходная формула расчета доходности может быть представлена в виде:

где d — доход, генерируемый активом (дивиденд, процент, прирост капитализированной стоимости);

I — регулярный доход от использования актива, полученный в виде процентов или дивидендов;

CI — величина инвестиций в актив.

В финансовом менеджменте используются следующие виды пока­зателей доходности:

• Фактическая доходность, рассчитываемая на основе фактиче­ски полученных данных и имеющая значение лишь для ретро­спективного анализа.

• Ожидаемая доходность, рассчитываемая на основе прогнозных данных в рамках имитационного перспективного анализа и ис­пользуемая для принятия решения о целесообразности приобре­тения тех или иных ценных бумаг.

Алгоритм расчета доходности актива может представлен следую­щим образом:

где dt — общая доходность; ds — текущая доходность; dc — капитализированная доходность;

Р0 — цена приобретения актива;

Рт — ожидаемая цена реализации актива;

I — регулярный доход от использования актива, полученный в виде процентов или дивидендов.

Предприниматель год назад приобрел акцию предприятия по цене 15 руб. Рыночная цена акции на текущий момент равна 16,7 руб., ди­

виденды по акции за год составили 1 руб. Определить общую доход­ность актива для предпринимателя.

Решение:

В сравнительном анализе при выборе вариантов инвестирования в те или иные облигации используется показатель доходность облига­ции без права досрочного погашения (YTM) (доходность к погаше­нию), который определяется по формуле:

где N — номинал облигации;

Р0 — текущая цена (на момент оценки);

Ik — купонный доход;

t — число лет, оставшихся до погашения облигации.

Рассчитать доходность облигации нарицательной стоимостью 1000 руб. с годовой купонной ставкой 9%, имеющую рыночную цену 840 руб. Облигация будет приниматься к погашению через 8 лет.

Решение:

При сравнении доходности YTM облигаций с различной частотой начисления процентов — годовое, квартальное, ежемесячное и т.д. — необходимо перейти от номинальной ставки (dn) к эффективной (de). Эффективная ставка может быть рассчитана по формуле:

где dn -номинальная годовая процентная ставка (доходность); de -эффективная годовая процентная ставка; m-количество начислений процентов в год.

Оценка доходности на момент отзыва облигации с рынка или ее досрочного погашения производится помощью показателя доходность облигации с правом досрочного погашения (YTC).

Расчет YTC осуществляется на основе формулы оценки безотзыв­ной облигации с постоянным доходом с выплатой процентов каждые полгода, в которой номинал заменен выкупной ценой Pm.

Облигация с нулевым купоном нарицательной стоимостью 1000 руб.

Доходность облигации с нулевым купоном рассчитывается на ос­нове формулы ее оценки:

Приобретение облигации является невыгодным вложением капита­ла, так как доходность данной облигации (8,2%) меньше альтернатив­ной (10%).

Облигация номиналом 1000 руб. и погашением через 10 лет была выпущена 3 года назад. В настоящее время ее цена равна 1050 руб. Проценты выплачиваются каждые полгода по ставке 14% годовых. В проспекте эмиссии указано, что в течение 5 лет предусмотрена защита от досрочного погашения. Выкупная цена превышает номинал на сум­му годовых процентов. Рассчитать YTM, YTC.

До погашения облигации осталось 7 лет, через 2 года облигация может быть досрочно погашена эмитентом (защита от досрочного по­гашения предусмотрена в течение 5 лет, с момента выпуска облигации прошло 3 года). Каждые полгода выплачивается купонный доход в

Доходность облигации без права досрочного погашения, или до­ходность к погашению (YTM), определяется с помощью функции Ex­cel «Подбор параметра» на основе формулы оценки безотзывной обли­гации с постоянным доходом с выплатой процентов каждые полгода:

облигации за период, прошедший с момента эмиссии (3 года), снизи­лась с 14 до 12,84%.

Доходность облигации с правом досрочного погашения (YTC) осуществляется с помощью функции Excel «Подбор параметра» на основе формулы оценки безотзывной облигации с постоянным дохо­дом с выплатой процентов каждые полгода, в которой номинал (N) заменен выкупной ценой (Pm = 1000 + 1000 * 0,14 = 1140 руб.):

Доходность к погашению (YTM) намного меньше доходности обли­гации с правом досрочного погашения (YTC): 12,89%

Источник

Доходность финансовых активов

1. Доходность финансового актива: виды и оценка

1.1 Финансовый актив и доходность

С операциями по финансовым активам сталкивается практически любой предприниматель. Крупные компании находят на рынке капитала дополнительные источники финансирования, рыночные индикаторы дают достаточно объективную оценку текущего и, главное, ожидаемого финансового положения эмитентов. В подавляющем большинстве компании прибегают к операциям с ценными бумагами в целях хеджирования, спекулирования и др. Поэтому знание основных рыночных индикаторов и алгоритмов, их расчет является обязательным для любого бизнесмена, финансового менеджера, аналитика.

Финансовый актив, как и любой товар, продающийся на рынке, имеет несколько характеристик, определяющих целесообразность операций купли / продажи с этим специфическим товаром. В отличие от обычных, потребительских товаров финансовые активы приобретаются не с целью их фактического потребления, а с намерением в дальнейшем получить либо регулярный доход, генерируемый данным активом (например, проценты, дивиденды), либо спекулятивный доход (доход от операций купли / продажи). Поэтому наибольший интерес представляют такие характеристики финансового актива, как стоимость, цена, доходность, риск.

Стоимость представляет собой денежную оценку ценности данною актива. В специальной литературе нередко выделяют четыре стоимостные характеристики: ценность, стоимость, цена, себестоимость. Но мы не будем различать термины «стоимость» и «ценность», а для характеристики стоимостной оценки актива будем использовать термин «стоимость».

Стоимость (ценность) не является абсолютно однозначной характеристикой; приведем следующий пример, некая раритетная вещица, продающаяся на рынке, может, с одной стороны, иметь исключительно высокую ценность для коллекционера, а, с другой стороны, не представлять никакого интереса для обычного посетителя рынка. Поэтому любой товар, а том числе и финансовый актив, может иметь несколько оценок стоимости.

Цена – это некоторая денежная оценка актива, по которой его можно купить (продать) в данный момент.

Можно сформулировать несколько условных правил, позволяющих провести определенное различие между ценой и стоимостью финансового актива:

а) стоимость – расчетный показатель, а цена – декларированный, т.е. объявленный, который можно видеть в прейскурантах, ценниках, котировках;

б) в любой конкретный момент цена однозначна, а стоимость многозначна, при этом число оценок стоимости зависит от числа профессиональных участников рынка и формы эффективности рынка;

в) с известной долей условности можно утверждать, что стоимость первична, а цена вторична, поскольку в условиях равновесного рынка цена, во-первых, количественно выражает внутренне присущую активу стоимость и, во-вторых, стихийно устанавливается как среднее из оценок стоимости, рассчитываемых инвесторами.

Из приведенных рассуждений видно, каким образом могут осуществляться операции купли / продажи финансовых активов: потенциальный покупатель некоторым образом рассчитывает стоимость актива и сравнивает ее с декларированной ценой.

Так же помимо цены и стоимости существуют и другие немаловажные для инвестора характеристики актива – это показатели его доходности.

Доходность финансового актива – это годовая процентная ставка, отражающая отдачу на капитал, вложенный в данный актив. В литературе используется также синоним данного термина – норма прибыли. Это относительный показатель, выражаемый в терминах годовой процентной ставки и рассчитываемый соотнесением некоторого относимого к году дохода (INC), генерируемого данным активом, с величиной исходной инвестиции (IС) в него, т.е. в наиболее общем виде этот показатель может быть представлен следующим образом:

В операциях на финансовых рынках именно доходность (а не доход, генерируемый активом) является наиболее востребованной характеристикой финансового актива. Дело в том, что любой доход (а в этом качестве может выступать дивиденд, процент, прирост капитализированной стоимости), который можно было бы использовать как индикатор целесообразности и эффективности операции с данным активом, обладает одним весьма существенным недостатком – он является абсолютным показателем, а потому практически не пригоден для пространственно-временных сопоставлений. Иное дело доходность – это уже относительный показатель, разумный коридор изменения которого в устойчиво развивающейся экономике, не подверженной экстремальным колебаниям, не только поддается оценке, но и является инвариантным для ценных бумаг любых эмитентов.

Для понимания логики расчета показателей доходности финансового актива и соответствующих вычислительных алгоритмов рассмотрим прогнозный (плановый) период, равный одному году (рис 1). Предположим, что, во-первых, актив можно купить в начале года по цене Р_0, во-вторых, актив обещает по истечении года получение регулярного дохода в сумме D₁ – в-третьих, актив можно будет продать в конце года по цене Р₁. Заметим, что условие о регулярном доходе не является обязательным (например, облигация с нулевым купоном не предусматривает выплату регулярного дохода, но продается с дисконтом, величина которого зависит от срока погашения облигации). В любом случае значении показателей D₁ и P₁ являются прогнозными.

Между показателями цены и регулярного дохода, относящимся к одному моменту времени, существуют определенные и невполне очевидные соотношения, а потому уместно сделать следующий комментарий. Р₀ можно назвать экс-доходной ценой, т.е. ценой, в которую не вводит регулярный доход D₀ начисленный к выплаченный по итогам предшествующего периода. Иными словами, цена P₀, выражает ценность финансового актива с позиции будущего, т.е. ожидаемых доходов, а не тех доходов, которые имели место в прошлом. Точно так же цена P₁, будет отражать ценность актива в момент времени 1 с позиции будущих доходов (D₂, D₃ и т.д.). т.е. доход D₁ к ней не относится, в ее формировании не участвует. Сделанное замечание имеет особое значение при совершении операций с акциями, по которым предусматривается выплата дивидендов. В этом случае регулярным доходом является дивиденд, а цена Р₀ называется экс-дивидендной ценой, если к цене Р₀ прибавить дивиденд D₀, то полученная стоимостная оценка называется дивидендной ценой акции.

Обычно Р₁ > Р₀, хотя выполнение этого неравенства не является обязательным: если по итогам периода имеет место обратное неравенство, говорят: об убытке от капитализации и соответствующей ему отрицательной доходности.

Итак, при приобретении актива будет иметь место отток денежных средств в сумме Р₀, а по окончании года – приток в сумме регулярного дохода D₁ и текущей цены актива Р₁. Очевидно, что общий доход, генерируемый инвестицией Р₀, в планируемом году составит величину D₁ + (P₁ – P₀)), а общая доходность (total expected rate of return) будет равна:

Первое слагаемое (k_d) в формуле представляет собой текущую доходность (current yield), в приложении к акциям она называется также дивидендной (dividend yield); второе слагаемое (k_c) носит название капитализированной доходности (expected capital gains yield) Из. приведенной формулу хорошо видно, что общий доход (или общая доходность) имеет два компонента, причем в зависимости от успешности работы и стратегии развития компании, эмитировавшей данный актив, весомость того или иного компонента может быть разной. Таким образом, выбирая для покупки активы, эмитированные той или иной компанией инвестор должен расставить для себя приоритеты – что важнее, доход регулярный или доход от прироста капитала. Ни один из показателей доходности в правой части не может использоваться как обобщающая характеристика эффективности инвестирования в конкретный финансовый актив, в этой роли выступает лишь показатель общей доходности.

В общем случае показатель доходности можно трактовать как годовую процентную ставку, уравновешивающую исходную инвестицию в актив с генерируемым им денежным (возвратным) потоком. Это эффективная годовая процентная ставка, характеризующая экономическую целесообразность данной финансовой операции.

В зависимости от вида финансового актива генерируемый им возвратный поток может быть различным.

Так, для бессрочной облигации все элементы возвратного потока одинаковы. Несложно заметить, что в зависимости от намерений инвестора в отношении действий с активом может меняться как вид возвратного потока, так и значение показателя доходности.

В зависимости от вида финансового актива и абсолютных показателей, выбранных для его характеристики, можно исчислить несколько числовых характеристик доходности. Поскольку их значения могут существенно различаться, нельзя говорить о некой абстрактной доходности, необходимо обязательно уточнять, о чем идет речь, какой алгоритм используется для расчета.

1.2 Доходность облигации

Доходность срочной облигации без права досрочного погашения. Оценка стоимости подобной облигации выполняется по формуле; эта же формула, может использоваться для оценки доходности отзывной облигации. Предполагается, что в этой формуле известны все показатели, кроме r; напомним, что в левой части в этом случае берется текущая рыночная цена актива Р_m:

СF – сумма регулярно выплачиваемого процентного дохода за базисный период; n – число базисных периодов погашения облигации,

М – нарицательная стоимость облигации;

P_m – рыночная цена облигации па момент ее приобретения (фактического или условного).

Разрешая уравнение относительно r, определяем общую доходность данной облигации. Этот показатель иногда называют доходностью к погашению и обозначают YTM – по аналогии с англоязычной терминологией (yield to maturity). Финансовые аналитики пользуются также более простым спо

Источник