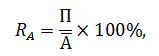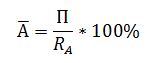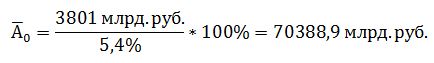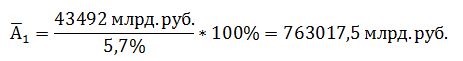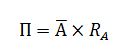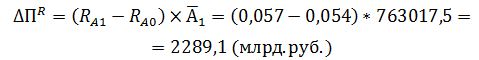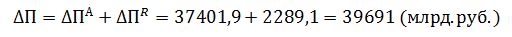Доходность активов задачи с решением

Задача

Имеются данные о финансовой деятельности организаций Российской Федерации:

1. Сальдированный финансовый результат (прибыль минус убыток), млрд. руб.

По приведенным данным определите за каждый год:

а) среднегодовую стоимость активов;

б) изменение прибыли за счет изменения двух факторов: рентабельности активов и среднегодовой стоимости активов (в абсолютном и относительном выражении).

Проанализируйте полученные результаты и сделайте выводы.

Решение

Рентабельность активов определяется по следующей формуле:

где: П – прибыль;
А – среднегодовая стоимость активов.

Отсюда среднегодовая стоимость активов равна:

Среднегодовая стоимость активов в базисном году:

Среднегодовая стоимость активов в отчетном году:

Влияние факторов на прибыль оценивается с помощью факторной модели:

Изменение прибыли за счет увеличения среднегодовой стоимости активов:

Изменение прибыли за счет повышения рентабельности активов:

Общее изменение прибыли:

Выводы: в отчетном году произошло резкое увеличение стоимости активов по сравнению с базисным годом. Это привело к увеличению размера финансового результата на 37401,9 млрд. руб. Повышение рентабельности также положительно повлияло на финансовый результат – он увеличился на 2289,1 млрд. руб. Общее увеличение прибыли в отчетном году составило 39691 млрд. руб. по сравнению с базисным годом.

Источник

Задачи на определение прибыли и рентабельности

Рентабельность продаж пример расчета

1 Задача. Рассчитайте годовую прибыль предприятия , если доход за год составил 2,5 млн рублей, годовые переменные издержки составили 0,5 млн рублей, постоянные издержки составили 1,2 млн рублей. Рассчитайте рентабельность продаж.

Решение задачи на расчет прибыли

Прибыль и рентабельность расчет.

Прибыль рассчитывается по формуле:

Прибыль=Доход – Общие издержки

Следовательно прибыль = 2,5- (0,5+1,2)=0,8 млн руб или 800 тыс. руб.

Расчет рентабельности продаж.

Рентабельность продаж находят по формуле:

Формула рентабельности: Рентабельность продаж = Прибыль / Общий доход = 0,8 / 2,5=0,32 или 32%.

Вывод по расчету рентабельности: Работа предприятия может рассматриваться эффективной при рентабельности продаж в 15%. В нашем примере рентабельность составляет 32%, следовательно уровень рентабельности очень хороший.

Рассмотрим еще один пример расчета рентабельности продаж.

2 Задача. Найдите прибыль и определите рентабельность продаж продуктового магазина за месяц, если выручка за данный месяц составила 4 500 000 рублей, средняя наценка на товары составила 22%. Затраты на покупку товаров для продажи: 3510 000 рублей, заработную плату за месяц составили 400 000 рублей, затраты на арендную плату и коммунальные услуги: 230 000 рублей.

Решение задачи. Итак, рассчитаем прибыль и рентабельность продаж.

Наценка составила 22%. Значит прибыль предприятия за период будет равна 22% от 4 500 000 рублей, т.е. 0,22*4500 000 = 990 000 рублей.

Однако если наценка добавляется к себестоимости товаров (как правило, определяемой исходя из прайслиста поставщиков), то предприятие еще из прибыли должно выплатить заработную плату, оплатить коммунальные услуги и погасить постоянные затраты (арендная плата)

Поэтому прибыль уменьшится на данные затраты.

Реальная прибыль будет равна 990000-400000-230000=360 000 рублей.

Чистая прибыль (за минусом налога на прибыль) = 360 000 – 0,2*360 000 =288000 рублей.

Итак, наценка составила 22%.

А рентабельность (прибыльность) продаж будет значительно ниже.

Найдем рентабельность продаж по валовой прибыли и по чистой прибыли.

Рентабельность продаж рассчитывается по формуле:

Формула рентабельности: Рентабельность продаж = Прибыль / Выручка.

Тогда рентабельность продаж по валовой прибыли = Валовая прибыль / Выручка = 360 000 / 4500 000 =0,08 или 8%.

Рентабельность продаж по чистой прибыли = Чистая прибыль / Выручка = 288 000 / 4500 000 = 0,064 или 6,4%.

Выводы рентабельности продаж: Нормальным считается значение рентабельности, превышающее 15%. Поскольку рентабельность продаж предприятия по валовой прибыли составила 8%, а по чистой прибыли 6,4%, то магазин работает недостаточно эффективно. Следует повысить среднюю наценку на реализуемую продукцию.

Данный пример предназначен для практических занятий. к.э.н., доцент Одинцова Е.В.

Источник

Задача №592 (расчет рентабельности)

Определите рентабельность активов и источников собственных средств фирмы, если прибыль за год составила 1800 тыс. рублей, а валюта баланса на начало года составляла 36090 тыс. рублей, в том числе собственный капитал фирмы 12070 тыс. рублей, на конец года валюта баланса составила 39800 тыс. рублей, в том числе собственный капитал фирмы 13100 тыс. руб.

Рекомендуемые задачи по дисциплине

Задача №458 (расчет коэффициентов ликвидности)

Имеются следующие данные: денежные средства – 70 тыс. руб.; краткосрочные финансовые вложения – 28 тыс. руб.; дебиторская задолженность – 130 тыс.

Задача №592 (расчет рентабельности)

Определите рентабельность активов и источников собственных средств фирмы, если прибыль за год составила 1800 тыс. рублей, а валюта баланса на.

Задача №837 (расчет денежного потока)

Определите, чему равен денежный поток от операционной деятельности (на основе данных косвенного кэш-фло). Проведите все необходимые расчеты. За.

Задача №608 (составление баланса на основе финансовых коэффициентов)

Составьте баланс предприятия при следующих данных: коэффициент автономии = 0,5; коэффициент фондоотдачи всех внеоборотных активов = 3,5; коэффициент.

Задача №273 (диагностика финансовой устойчивости)

Выполнить финансовую диагностику предприятия по данным таблицы. Оценить финансовую устойчивость предприятия. Исходные данные: Наименование показателя на.

Рентабельность – относительный показатель экономической эффективности. Рентабельность комплексно отражает степень эффективности использования материальных, трудовых и денежных ресурсов, а также природных богатств. Коэффициент рентабельности рассчитывается как отношение прибыли к активам, ресурсам или потокам, её формирующим. Может выражаться как в прибыли на единицу вложенных средств, так и в прибыли, которую несёт в себе каждая полученная денежная единица. Показатели рентабельности часто выражают в процентах.

Рентабельность активов – относительный показатель эффективности деятельности, частное от деления чистой прибыли, полученной за период, на общую величину активов организации за период. Один из финансовых коэффициентов, входит в группу коэффициентов рентабельности. Показывает способность активов компании порождать прибыль.

Для расчета рентабельности активов используют следующую формулу:

где П – прибыль, руб.,

А – среднегодовая величина активов, руб.

Активы (валюта баланса) на начало года составляли 36090 тыс. руб., на конец года – 39800 тыс. руб. Следовательно, среднегодовая величина активов равна:

А=(36090+39800)/2=37945 тыс. руб.

Рентабельность активов равна:

Рентабельность собственного капитала – относительный показатель эффективности деятельности, частное от деления чистой прибыли, полученной за период, на собственный капитал организации. Это один из финансовых коэффициентов, входит в группу коэффициентов рентабельности. Показывает отдачу на инвестиции акционеров с точки зрения учетной прибыли.

Для расчета рентабельности собственного капитала используют следующую формулу:

где П – прибыль, руб.,

СК – среднегодовая величина собственного капитала, руб.

Собственный капитал на начало года составлял 12070 тыс. руб., на конец года – 13100 тыс. руб. Следовательно, среднегодовая величина собственного капитала равна:

СК=(12070+13100)/2=12585 тыс. руб.

Рентабельность собственного капитала равна:

Таким образом, 1 руб. средств, вложенных в имущество (активы) предприятия обеспечивает получение прибыли в размере 4,7 коп.; а 1 руб. средств, сложенных в собственный капитал, обеспечивают получение прибыли в размере 14,3 коп.

Источник

Задача №460 (расчет рентабельности активов)

Активы предприятия составляют 115 млн. руб., выручка от продаж – 196 млн. руб., рентабельность продаж – 14,5%. Определите рентабельность активов.

Рекомендуемые задачи по дисциплине

Задача №458 (расчет коэффициентов ликвидности)

Имеются следующие данные: денежные средства – 70 тыс. руб.; краткосрочные финансовые вложения – 28 тыс. руб.; дебиторская задолженность – 130 тыс.

Задача №592 (расчет рентабельности)

Определите рентабельность активов и источников собственных средств фирмы, если прибыль за год составила 1800 тыс. рублей, а валюта баланса на.

Задача №837 (расчет денежного потока)

Определите, чему равен денежный поток от операционной деятельности (на основе данных косвенного кэш-фло). Проведите все необходимые расчеты. За.

Задача №608 (составление баланса на основе финансовых коэффициентов)

Составьте баланс предприятия при следующих данных: коэффициент автономии = 0,5; коэффициент фондоотдачи всех внеоборотных активов = 3,5; коэффициент.

Задача №273 (диагностика финансовой устойчивости)

Выполнить финансовую диагностику предприятия по данным таблицы. Оценить финансовую устойчивость предприятия. Исходные данные: Наименование показателя на.

Рентабельность продаж определяется по формуле:

где П – прибыль, млн. руб.;

В – выручка от продаж, млн. руб.

Из этой формулы выражаем величину прибыли:

П=В*Рпр/100=196*14,5/100=28,42 млн. руб.

Рентабельность активов рассчитывается по формуле:

где А – среднегодовая стоимость активов предприятия, млн. руб.

Таким образом, 1 руб. активов предприятия дает прибыль в размере 24,71 коп. в год.

Обновить

Задачи

ПОДСКАЗКА!
Для заполнения
формы заказа
переходите по ссылке
Решение задачи
————>
Стоимость любой задачи —
50 руб.
Фрагменты решения
————>
Подробности и
ФОРМА ЗАКАЗА

Анализ финансового состояния российских компаний

Период анализа — 3 года
(например, 2018-2020 гг.)

Использована официальная отчетность компаний

Коэффициенты, таблицы,
рисунки, выводы.

Горизонтальный и вертикальный анализ баланса,
анализ ликвидности и платежеспособности,
анализ финансовой устойчивости,
анализ финансовых результатов и рентабельности,
анализ вероятности банкротства
и другие разделы
от 50 руб.

БЕСПЛАТНАЯ демонстрационная версия отчета

Предлагаем воспользоваться консультацией по решению задач, условия которых размещены на страницах сайта. Стоимость одной задачи — 50 рублей.

Все задачи УЖЕ решены. Под условием каждой задачи Вы можете увидеть ФРАГМЕНТЫ решения.

Файл с задачей высылается в формате Word и предполагает максимально подробные пояснения выполненных расчетов и полученных результатов.

Для получения подробной информации и заказа переходите по ссылке «Решение задачи», размещенной под условием каждой задачи.

С уважением, администратор сайта.

Предлагаем ознакомиться с информацией о выполненных работах по финансовому анализу российских компаний:

1. Каждая работа по финансовому анализу состоит из 10-ти разделов по банкам и 12-ти разделов по остальным компаниям..

2. Общий объем — от 80 до 120 страниц (методика, таблицы, рисунки, анализ всех показателей, выводы).

3. Стоимость любого раздела — 50 руб. или вся работа за 500 руб. У Вас есть возможность заказать только нужные Вам разделы работы.

4. Расчеты выполнены по самой последней опубликованной отчетности компании с официального сайта. Отчетность к работе прилагается.

5. Оплата производится только после ознакомления с демонстрационной версией работы.

6. Все интересующие Вас вопросы можно задать в переписке с автором работы.

Источник

Доходность активов задачи с решением

Решения задач для 5.0

Уставный капитал компании составляют 500 тыс. обыкновенных и 100 тыс. привилегированных акций. Прибыль компании до уплаты налогов равна 10 млн. руб., а величина налога на прибыль – 3 млн. руб. Величина дивиденда по привилегированным акциям составляет 4 руб. на одну акцию. Рассчитайте значение показателя EPS.

EPS (Earning per share) – прибыль на одну акцию.

1. Определим чистую прибыль 10-3=7 млн.р.

2. Определим сумму дивидендов по привилегированным акциям 4*100 000 = 400 тыс. руб.

3. Определим прибыль, доступную акционерам обыкновенных акций

7 000 000 – 400 000 = 6,6 млн. руб.

4. Доход на 1 обыкновенную акцию 6 600 000 / 500 000 = 13,2 рубля .

Уставный капитал компании составляет 300 тыс. руб. Продано всего 1500 акций, в том числе 1250 акций обыкновенных и 250 акций привилегированных с одним и тем же номиналом. Общая сумма чистой прибыли, подлежащая распределению в виде дивидендов, 31 тыс. руб. По привилегированным акциям фиксированная ставка дивиденда утверждена в размере 20% от номинала. Рассчитать сумму дивиденда на обыкновенную акцию.

1. Определим номинал акций 300 000 / 1500 = 200 рублей.

2. Определим сумму дивидендов по привилегированным акциям 200 * 0,2 * 250 =

3. Определим прибыль, доступную акционерам обыкновенных акций 31 – 10 = 21 тыс. руб.

4. Дивиденд на 1 обыкновенную акцию 21 000 / 1250 = 16,8 рублей.

Номинал обыкновенных акций компании составляет 20 руб., величина дохода на одну акцию и дивиденд составляет 80 руб. и 50 руб. соответственно, рыночная цена и балансовая стоимость акции равна 150 руб. и 500 руб., соответственно, а величина денежного потока на акцию составляет 100 руб. Каким будут значения P/E и дивидендной доходности по акциям этой компании?

1. P/E (ernings multiple) – коэффициент цена/прибыль.

2. P/E = 150 / 80 = 1,875 рублей

3. Дивидендная доходность 50 / 150 = 0,333

По итогам года по акции выплачен дивиденд в размере 11,5 руб. на акцию. Предполагается, что прибыль и дивиденды будут расти в дальнейшем на 5% в год. Используя модель роста дивидендов, оцените стоимость акции в рублях, если ожидаемая доходность по акции составляет 14,3%

1. Стоимость 11,5 х (1 + 0,05) / (0,143 – 0,05) = 129,84 руб.

Величина дивиденда, выплаченного по итогам финансового года составляет 3,5 руб. Годовой темп роста дивиденда за последнее время составил 14 %. Ожидаемая доходность акции 25,4 %. Пользуясь моделью постоянного роста дивиденда оцените стоимость акции в рублях.

1. Стоимость 3,5 х (1 + 0,14) / (0,254 – 0,14) = 35

По итогам года по акции выплачен дивиденд в размере 32.5 руб. на акцию. Предполагается, что прибыль и дивиденды будут расти в дальнейшем на 12% в год. Используя модель роста дивидендов, оцените стоимость акции в рублях, если ожидаемая доходность по акции составляет 16,3 %.

1. Стоимость 32,5 * (1+0,12) / (0,163 – 0,12) = 846,51

По итогам года чистая прибыль на акцию составила EPS = 9,63 руб., были выплачены дивиденды на акцию в размере DPS = 6 рублей. Рентабельность капитала составляет ROE = 28,5%. Доходность акции, рассчитанная по методу CAPM, составляет 24,6%. Считая, что предприятие придерживается стабильной политики реинвестирования прибыли, оценить темпы роста прибыли и дивидендов предприятия.

1. Определим коэффициент реинвестирования (9,63 – 6) / 9,63 = 0,3769

2. Темп роста (хотя это с трудом можно назвать темпом роста) 0,3769 * 0,285 = 0,1074

По итогам года чистая прибыль на акцию составила EPS = 10.46 руб., были выплачены дивиденды на акцию в размере DPS = 2 руб. Рентабельность капитала составляет ROE = 23,5%. Предполагается, что предприятие будет придерживаться стабильной политики реинвестирования прибыли, поэтому прибыль будет расти с постоянным темпом роста. Доходность акции, рассчитанная по методу САРМ, составляет 23,5%. Оцените темпы роста прибыли и дивидендов предприятия.

1. Определим коэффициент реинвестирования (10,46-2) / 10,46 = 0,8088

2. Темп роста 0,8088 * 0,235 = 0,1901

По итогам года чистая прибыль на акцию составила EPS = 10,5 руб., были выплачены дивиденды на акцию в размере DPS = 4,5 руб. Рентабельность капитала составляет ROE = 28%. Доходность акции, рассчитанная по методу САРМ составляет 25%. Считая, что предприятие будет придерживаться стабильной политики реинвестирования прибыли, оцените темпы роста прибыли и дивидендов.

1. Определим коэффициент реинвестирования (10,5 – 4,5) / 10,5 = 0,5714

2. Темп роста 0,5714 * 0,28 = 0,16

Облигация с фиксированным купоном, равным 20% от номинала и выплачиваемым ежегодно, куплена по полному курсу 90. Срок облигации 10 лет. Какова простая доходность к погашению?

1. Простая доходность к погашению (((20 * 10) + (100-90)) / 90) / 10 = 0,23

облигация с фиксированным купоном, равным 12,5% от номинала и выплачиваемым ежегодно, куплена по полному курсу 102,34. Срок облигации 5 лет. Какова простая доходность к погашению?

1. Простая доходность к погашению (((12,5 * 5) + (100 – 102,34)) / 102,34) / 5 = 0,1176

Облигация с фиксированным годовым купоном, равным 9,5% от номинала и выплачиваемым ежеквартально, куплена по полному курсу 88,54. Срок облигации 6 лет. Какова простая доходность к погашению?

1. Простая доходность к погашению (((9,5 * 6) + (100 – 88,54)) / 88,54) / 6 = 0,1289

Номинал облигации с фиксированным купоном равен 1200 руб., годовой купонной доход составляет 180 руб., срок облигации 9 лет. По какой максимальной цене в рублях следует приобрести облигацию, чтобы простая доходность составила не менее 17%?

1. Определим максимальную цену ((180 * 9) + (1200 – Х)) / Х = 0,17*9

Номинал облигации с фиксированным купоном равен 250 руб., годовой купонный доход составляет 70 руб., срок облигации 4 года. По какой максимальной цене в рублях следует приобрести облигацию, чтобы простая доходность составила не менее 9,39%?

1. Максимальная цена ((70х4)+(250-Х))/Х=0,0939*4

Номинал облигации с фиксированным купоном равен 500 руб., годовой купонный доход составляет 140 руб., срок облигации 6 лет. По какой максимальной цене в рублях следует приобрести облигацию, чтобы простая доходность составила не менее 12,83%?

1. Максимальная цена ((140*6)+(500-Х)/Х=0,1283*6

Срок облигации с фиксированным купоном равен 7 годам. Купонный доход выплачивается ежегодно по норме 12% от Номинала в год. Найти курс облигации, если ставка дисконтирования принята равной 16 %.

1. Курс облигации ((0,12*7)/ 1,16 3.5 ) + (1/1.16 7 ) = 0.8535 => 83.85

Срок облигации с фиксированным купоном равен 6 годам. Купонный доход выплачивается ежегодно по норме 11% от номинала в год. Найти курс облигации, если ставка дисконтирования принята равной 12,45%.

1. Курс облигации ((0.11*6)/1,1245 3 ) + (1/1.1245 6 ) = 0.9587 => 94.11 (см.9.х.16)

Срок облигации с фиксированным купоном равен 7 годам. Купонный доход выплачивается ежеквартально по норме 5,3% от номинала в год, номинал составляет 1000 рублей. Найти текущую цену облигации в рублях, если ставка дисконтирования принята равной 4,75 %.

Корректного решения этой задачи у нет (мой ответ 1031.157), поэтому просто запоминаем 1032.59

До погашения бескупонной дисконтной облигации осталось 3 месяца. Найти рыночный курс облигации, если ставка дисконтирования выбрана 15,3%.

1. Рыночный курс 100 / (1+0,153) 3/12 = 96.50

До погашения бескупонной дисконтной облигации осталось 3 года и 7 месяцев, номинал облигации 1000 руб. Найти рыночную стоимость облигации (в рублях), если ставка дисконтирования выбрана 10,4%.

1. Рыночная стоимость 1000 / (1+0,104) 3.583 = 701.50

До погашения бескупонной дисконтной облигации осталось 3 года и 3 месяца, номинал облигации 250 руб. Найти рыночную стоимость облигации (в рублях), если ставка дисконтирования выбрана 8,5%.

1. Рыночная стоимость облигации 250 / (1+0,085) 3.25 = 191.78

Номинал бескупонной облигации равен 1250 руб., срок 3 года и 3 месяца. По какой цене (в рублях) следует приобрести облигацию, чтобы доходность с использованием простого процента составила не менее 14%?

1. Цена 1250 / (1+(0,14х3)+(0,14х3/12)) = 859,11

Номинал бескупонной облигации равен 1000 руб., срок 3 года и 7 месяцев. По какой цене (в рублях) следует приобрести облигацию, чтобы доходность с использованием простого процента составила не менее 12%?

1. Цена 1000 / (1+(0,12х3)+(0,12х7/12))= 699,30

Срок бескупонной облигации 3 года и 3 месяца. По какому курсу следует приобрести облигацию, чтобы доходность с использованием простого процента составила не менее 13%?

Чистый курс облигации 103,45, годовой купонный доход составляет 23% от номинала, срок облигации 5 лет. Найти простую доходность к погашению с учетом налогообложения, считая, что налог на дисконт составляет 15%, налог на купонный доход 20%.

1. Простая доходность к погашению (0,23*0,8*5 – 0,0345)/1,0345 = Х*5

Чистый курс облигации 103,45, годовой купонный доход составляет 23% от номинала, срок облигации 5 лет. Найти простую доходность к погашению с учетом налогообложения, считая, что налог на дисконт и на купонный доход составляет 24%.

1. Простая доходность к погашению (0,23*0,76*5-0,0345)/1,0345=Х*5

Чистый курс облигации 94,57, годовой купонный доход составляет 10% от номинала, срок облигации 4 года. Найти простую доходность к погашению с учётом налогообложения, считая, что налог на дисконт оставляет 20 %, налог на купонный доход 30%.

1. Простая доходность к погашению (0,1*0,7*4-0,0543*0,8)/0,9457=Х*4

Облигация с переменным купоном давала в течение четырёх лет следующие купонные доходы: 850 руб., 790 руб., 830 руб., 870 руб., затем (в конце четвёртого года) была погашена по номиналу 10000 руб. Найти реализованную доходность облигации, если облигация была куплена за 9800 руб.

1. Реализованную доходность правильно считать так:

(850/(1+Х)^1 + 790/(1+Х)^2 + 830/(1+Х)^3 + 870/(1+Х)^4 + 10 000/(1+Х)^4) = 9800

Решая это уравнение у вас получится уравнение с Х в 4 степени. После его решения и вычисления корней дискриминанта, вам надо будет выбрать 1 из корней, удовлетворяющих условию уравнения, он и будет ответом. Я решал такое уравнение на 1 листе А4, исписав его с 2ух сторон, что заняло у меня почти 30 минут))

2. (Более короткий и оптимальный способ для решения таких уравнений – это подставить вместо Х в указанном выше уравнении предлагаемые в тесте ответы)

3. Реализованная доходность (при большом разбросе ответов, можно рассчитать быстро, через простую доходность)

Облигация с переменным купоном давала в течение трех лет следующие купонные доходы: 15 руб., 16,2 руб., 17,35 руб., затем (в конце третьего года) была погашена по номиналу 100 руб. Найти реализованную доходность облигации, если облигация была приобретена 104, 34 руб.

1. Реализованная доходность ((15+16,2+17,35-4,34)/104,34)/3= 0,1412 => 14.2% (см. 9.х.28)

Облигация с переменным купоном давала в течение пяти лет следующие купонные доходы: 135 руб., 150,34 руб., 120,5 руб., 120,5 руб., 110,45 руб., затем (в конце пятого года) была погашена по номиналу 1000 руб. Найти реализованную доходность облигации, если облигация была приобретена за 1125 руб.

1. Реализованная доходность

((135+150,34+120,5+120,5+110,45-125)/1125)/5= 0,091 => 9.61% (см. 9.х.28)

Купонный доход облигации с переменным купоном в первый год равен 150 руб., срок облигации равен 5 годам, номинал 1000 руб. В дальнейшем предполагается общее понижение ставок, поэтому предполагается, что в оставшиеся годы купоны будут равны соответственно: 140 руб., 130 руб., 120 руб., 110 руб. Облигация приобретена за 990 руб. Какова предполагаемая доходность облигации к погашению?

1. Предполагаемая доходность (тоже надо подставлять из ответов, см. описание 9.х.28)

2. (Разброс ответов большой, поэтому считаем через простую доходность к погашению)

((150+140+130+120+110+10)/990)/5 = 0,1333 => 13.54%

Купонный доход облигации с переменным купоном в первый год равен 170 руб., срок облигации 4 года, номинал 1000 руб. В дальнейшем предполагается общее повышение ставок, поэтому предполагается, что в оставшиеся годы купоны будут равны соответственно: 180 руб., 190 руб., 200 руб. Облигация приобретена за 986,34 руб. Какова предполагаемая доходность облигации к погашению?

1. Предполагаемая доходность к погашению

((170+180+190+200+13,66)/986,34)/4=0,1910 => 18.80% (см. 9.х.28)

Номинал облигации 1200 руб., чистый курс облигации 95,75%, годовой купонный доход равен 17,5% от номинала, выплата купонов производится 2 раза в год и купонный период равен 184 дням. Какую полную цену в рублях заплатит покупатель облигации (не считая комиссионного вознаграждения брокеру), если до выплаты ближайшего купона осталось 93 дня?

1. Процент за полугодие17,5/2 = 8,75%

НКД 8,75*(184-93 / 184) = 4,33%

Номинал облигации 1000 руб., чистый курс облигации 95,75%, годовой купонный доход равен 17,5 % от номинала, выплата купонов производится 2 раза в год и купонный период равен 184 дня. Какую полную цену в рублях заплатит покупатель облигации (не считая комиссионного вознаграждения брокеру), если до выплаты ближайшего купона осталось 83 дня?

1. Процент за полугодие 17,5/2=8,75%

НКД 8,75*(184-83 / 184)=4,80%

Номинал облигации 500 руб., чистый курс облигации 101,25%, годовой купонный доход равен 11,5% от номинала, выплата купонов производится 4 раза в год и купонный период равен 91 день. Какую полную цену в рублях заплатит покупатель облигации (не считая комиссионного вознаграждения брокеру), если до выплаты ближайшего купона осталось 45 дня?

1. Процент за квартал 11,5/4=2,875%

НКД 2,875*(91-45 / 91)=1,45%

Компания выпустила бескупонную ценную бумагу сроком на 1 год и номиналом в 1000 руб. Какова текущая стоимость бумаги в рублях, если безрисковые облигации на тот же срок имеют доходность 6,2% годовых, коэффициент бета бумаги оценивается в 1,2, ожидаемая рыночная доходность 15,5%годовых.

1. Стоимость заемного капитала 6,2 + (15,5-6,2)*1,2 = 17,36%

2. Текущая стоимость бумаги 1000/1,1736= 852,08

компания выпустила бескупонную ценную бумагу сроком на 2 года номиналом в 250 руб. Какова текущая стоимость бумаги в рублях, если безрисковые облигации на тот же срок имеют доходность 5,4% годовых, коэффициент бета бумаги оценивается в 0,75, ожидаемая рыночная доходность 14,4% годовых.

1. Стоимость заёмного капитала: 5,4 + (14,4-5,4)*0,75 = 12,15%

2. Текущая стоимость бумаги 250 / (1,1215)^2 = 198,77

Компания выпустила бескупонную ценную бумагу сроком на 3 года и номиналом в 1000 руб. Какова текущая стоимость бумаги в рублях, если безрисковые облигации на тот же срок имеют доходность 5,7% годовых, коэффициент бета бумаги оценивается в 1,12, ожидаемая рыночная доходность 14,4% годовых.

1. Стоимость заёмного капитала 5,7 + (14,4-5,7)*1,12=15,44

2. Текущая стоимость бумаги 1000 / 1,1544^3 = 649.96

Срок бескупонной облигации 3,5 года, номинал 1000 руб. Безрисковые облигации на тот же срок имеют доходность 5,3% годовых, коэффициент бета бумаги оценивается в 1,27, ожидаемая рыночная доходность 13,7% годовых. Определите текущую стоимость облигации в рублях.

1. Стоимость заемного капитала 5,3 + (13,7-5,3)*1,27 = 15,97

2. Текущая стоимость облигации 1000 / 1,1597^3.5 = 595.41

Срок бескупонной облигации 4 года и 3 месяца, номинал 500 руб. Безрисковые облигации на тот же срок имеют доходность 5,7% годовых, коэффициент бета бумаги оценивается в 0,73, ожидаемая рыночная доходность 14,4% годовых. Определите текущую стоимость облигации в рублях.

1. Стоимость заемного капитала 5,7 + (14,4-5,7)*0,73 = 12,05

2. Текущая стоимость облигации 500 / 1,1205^4.25 = 308.29

Срок бескупонной облигации 2 года и 2 месяца, номинал 250 руб. Безрисковые облигации на тот же срок имеют доходность 4,9% годовых, коэффициент бета бумаги оценивается в 0,84, ожидаемая рыночная доходность 12,3% годовых. Определите текущую стоимость облигации в рублях.

1. Стоимость заемных средств 4,9 + (12,3-4,9)*0,84 = 11,116

2. Текущая стоимость бумаги 250 / 1,11116^2.16666 = 198.96

Курс бескупонной облигации равен 63,2. Срок облигации (время до погашения) 3 года 8 месяцев. Каким будет курс облигации, если доходность облигации увеличится на 40 пунктов (1 пункт доходности равен 0,01%)? База: 365 дней в году.

1. Курс 1 100 / (1+Х)^3.66666 = 63.2

2. Курс 2 100 / (1.1373)^3.66666 = 62.39

Имеется облигация с выплатой номинала и процентов в конце срока. Ставка купона 20%, начисление процентов по номинальной процентной ставке. Облигация была приобретена по курсу 87,66, срок облигации 7 лет. Найти доходность к погашению.

1. Доходность к погашению (в данном случае очень оригинальная, но экономический смысл имеет) (1+0,2 / 0,8766^0.1428571 “”(1/7)””) -1 = 0.2228

Имеется облигация с выплатой номинала и процентов в конце срока. Ставка купона 1 5%, начисление процентов по номинальной процентной ставке. Облигация была приобретена по курсу 104,25, срок облигации 8 лет. Найти доходность к погашению.

1. Доходность к погашению (1+0,15 / 1,0425^0.125) -1 = 0.1440

Имеется облигация с выплатой номинала и процентов в конце срока. Ставка купона 12,5%, начисление процентов по номинальной процентной ставке. Облигация была приобретена по курсу 1 10,74, срок облигации 3 года. Найти доходность к погашению.

1. Доходность к погашению (1+0,125 / 1,1074^0.3333333) -1 = 0.0874

До погашения облигации с постоянным купоном осталось 173 дня и одна купонная выплата. Номинал облигации 2000 руб., облигация приобретена по полной цене 2174,56 руб. Годовой купонный доход составляет 250 руб. купоны выплачиваются 1 раз в год, база: 365 дней. Какова доходность облигации к погашению?

1. Доходность к погашению 2250 / (1+X)^(173/365) = 2174.56

До погашения облигации с постоянным купоном осталось 58 дней и одна купонная выплата. Номинал облигации 1000 руб., облигация приобретена по полной цене 1080 руб. Годовой купонный доход составляет 320 руб. купоны выплачиваются 4 раза в год, купонный период: 90 дней, база: 365 дней. Какова доходность облигации к погашению?

1. Купон за квартал 320*3/12 = 80

2. Доходность к погашению 1080 / (1+X)^(58/365) = 1080

До погашения облигации с постоянным купоном осталось 135 дней и одна купонная выплата. Номинал облигации 250 руб., облигация приобретена по полной цене 253,64 руб. Годовой купонный доход составляет 30 руб. купоны выплачиваются 2 раза в год, купонный период: 183 дня, база: 365 дней. Какова доходность облигации к погашению?

1. Величина купона за полугодие 30*6/12=15

2. Доходность к погашению 265 / (1+X)^(135/365) = 253.64

Портфель облигаций содержит три вида облигаций и имеет следующую структуру: -50 облигаций по курсу 96,34 с номиналом 1000 руб. и с дюраций 15 лет; -140 облигаций по курсу 107,35 с номиналом 500 руб. и с дюраций 3 года; -400 облигаций по курсу 87,23 с номиналом 100 руб. и с дюраций 5 лет; Какова дюрация портфеля в годах?

1. Дюрация ( англ. duration — длительность) — это средневзвешенный срок потока платежей , причём весами являются дисконтированные стоимости платежей. Дюрация является важнейшей характеристикой денежного потока, определяющая чувствительность его текущей стоимости к изменению процентной ставки . Дюрация потока зависит не только от его структуры, но и от текущей процентной ставки. Чем выше ставка, тем меньше доля стоимости дальних выплат по сравнению с короткими и тем меньше дюрация, и наоборот, чем меньше ставка, тем больше дюрация потока платежей.

Понятие дюрации было введено американским учёным Ф. Маколи (F.R. Macaulay).

Портфель облигаций содержит три вида облигаций и имеет следующую структуру: -400 облигаций по курсу 90,38 с номиналом 100 руб. и с дюраций 2 года; -140 облигаций по курсу 112,37 с номиналом 500 руб. и с дюраций 16 лет; -400 облигаций по курсу 85,45 с номиналом 250 руб. и с дюраций 11 лет; Какова дюрация портфеля в годах?

1. Дюрация 400*100*0,9038*2+140*500*1,1237*16+400*250*0,8545*11 / 400*100*0,9038+140*500*1,1237+400*250*0,8545 = 11,34

Портфель облигаций содержит три вида облигаций и имеет следующую структуру: -25 облигаций по курсу 96,34 с номиналом 1000 руб. и с дюраций 15 лет; -150 облигаций по курсу 107,35 с номиналом 100 руб. и с дюраций 10 лет; -100 облигаций по курсу 87,23 с номиналом 500 руб. и с дюраций 2 года; Какова дюрация портфеля в годах?

1. Дюрация 25*1000*0,9634*15+150*100*1,0735*10+100*500*0,8723*2 / 25*1000*0,9634+150*100*1,0735+100*500*0,8723 = 7,27

Облигация с фиксированным купоном, равным 20% от номинала, куплена по курсу 93,05. Срок облигации 5 лет. Выплаты купонов происходят один раз в год. Найти дюрацию облигации в годах.

1. (Эти задачи явно шутка, потому как решить их можно только часа за 2, имея сильные математические способности, тем не менее, я расскажу 2 способа: один — это как их надо решать, второй — как их реально решить)

2. Оценим ставку дисконтирования по полной формуле 20/(1+r) + 20/(1+r)^2+20/(1+r)^3+20/(1+r)^4+120/(1+r)^5 = 93.05

Нереальными усилиями решим это уравнение и получим ответ r=0.2245

Можно использовать более простую формулу 20*5/(1+r)^2.5 + 100/(1+r)^5 = 93.05

И подставлять значения вместо r, в данном случае не получится, т.к. купон очень большой, а срок очень маленький.

3. Дюрация. 20/(1,2245)+40/1,2245^2+60/1.2245^3+80/1.2245^4+120*5/1.2245^5 / 93.05 = 3,54

Облигация с фиксированным купоном, равным 12,5% от номинала, куплена по курсу 107,60. Срок облигации 5 лет. Выплаты купонов происходят один раз в год. Найти дюрацию облигации в годах.

1. Ставка дисконтирования 12,5*5/(1+r)^2.5 + 100/(1+r)^5 = 107.60

Подставим 0,10 (111,34), 0,15 (93,79), 0,11(107,49, подойдёт + ответ округляем вверх)

2. Дюрация. 12,5/1,11+25/1,11^2+37.5/1.11^3+50/1.11^4+562.5/1.11^5 / 107.60 = 3.95 => 4.04 (разброс ответов очень маленький, поэтому лучше точно определить ставку, или просто запомнить этот ответ)

Облигация с фиксированным купоном, равным 14,5% от номинала, куплена по курсу 92,7. Срок облигации 5 лет. Выплаты купонов происходят один раз в год. Найти дюрацию облигации в годах.

1. Ставка дисконтирования 14,5*5 / (1+r)^2.5 + 100/(1+r)^5 = 92.7

Подставим 0,1(119.22), 0,2(86,15), 0,18 (91,64, подойдёт, но ответ существенно округлим вверх + это довольно опасно, т.к. купон большой, а срок маленький)

2. Дюрация. 14,5/1,18+29/1,18^2+43.5/1.18^3+58/1.18^4+572.5/1.18^5 / 92.7 = 3.66 => 3.84 (но опять же, если будет время, то лучше поколдовать над ставкой, подставив ее в полную формулу или запомнить)

Расположите перечисленные ниже облигации в порядке убывания их дюрации.

Есть следующие закономерности изменения дюрации:

· При прочих равных условиях, чем продолжительнее срок погашения облигации, тем больше дюрация.

· При прочих равных условиях, при повышении ставки дисконтирования дюрация купонных облигаций уменьшается.

· При прочих равных условиях, чем выше ставка купонных платежей по облигации, тем меньше дюрация.

Зная эти свойства, проведём группировку

1. Срок (красный и золотистый)

2. Доходность (зелёный и синий)

Итого: Облигация 3 (1,1,1), облигация 4 (1,1,2), облигация 1 (1,1,3), Облигация 2 (2,1,3), Облигация 5 (2,2,3)

Расположите перечисленные ниже облигации в порядке убывания их дюрации.

Расположите перечисленные ниже облигации в порядке убывания их дюрации.

Фондовый индекс состоит из акций трех компаний: А, В и С. Индекс рассчитывается как простое среднее арифметическое. Цены акций равны: А — 20 руб., В -35 руб., С — 30 руб. Делитель индекса составляет 2,2857. На следующий день изменяется состав индекса. Из него исключают акцию А и вместо неё включают акцию компании Е. Цена акции Е равна 40 руб. Определить новое значение делителя индекса

1. (Такие задачи можно решить пропорцией) (И вообще, для меня довольно странно, зачем давать задачи на расчёт индекса по средней арифметической)

2. Делитель индекса

20+35+30 / 2,2857 = 40+35+30 / Х

фондовый индекс состоит из акций трёх компаний: B, C и Е. Индекс рассчитывается как простое среднее арифметическое. Цены акций равны: В — 35 руб., С — 60 руб., Е — 40 руб. Делитель равен 2,2857. На следующий день в индекс включают акцию компании Р. Ее цена равна 50 руб. Определить новое значение делителя индекса.

1. Делитель индекса

135 / 2,2857 = 185 / Х

Фондовый индекс состоит из акций трёх компаний: В,С и Е. Индекс рассчитывается как простое среднее арифметическое. Цены акций равны: В — 35 руб., С — 60 руб., Е — 40 руб. Делитель равен 2,2857. На следующий день происходит выплата дивидендов по акции В акциями. Дивиденд равен 20%. Определить новое значение делителя индекса.

1. Делитель индекса

135 / 129,16 = 2,2857 / Х

Фондовый индекс состоит из акций трёх компаний: А, В и С. Индекс рассчитывается как среднее арифметическое, взвешенное по капитализации компаний. На момент начала расчёта индекса цена акции А была равна 15 руб., В — 20 руб., С- 40 руб. Количество выпущенных акций компании А составляло 100 штук, В — 200 штук и С- 350 штук. В момент времени Г цены акций составили: А — 25 руб., В — 30 руб., С — 50 руб. На основе значения индекса охарактеризовать рост стоимости акций за прошедший период.

1. Рост стоимости индекса 25*100+30*200+50*350 / 15*100+20*200+40*350 = 1,333333

Фондовый индекс состоит из акций трёх компаний: А, В и С. Индекс рассчитывается как среднее арифметическое, взвешенное по капитализации компаний. На момент начала расчёта индекса цена акции А была равна 25 руб., В — 30 руб., С — 55 руб. Количество выпущенных акций компании А составляло 200 штук, В — 300 штук и С — 400 штук. В момент времени Т цены акций составили: А — 32 руб., В — 45 руб., С -44 руб. Значение индекса в момент начала его расчёта принято равным 10. Определить значение индекса в момент времени Т.

1. Значение индекса в момент времени Т

32*200+45*300+44*400 / 25*200+30*300+55*400 = 1,041666

Фондовый индекс состоит из акций трёх компаний: А, В и С. Индекс рассчитывается как среднее арифметическое, взвешенное по капитализации компаний. На момент начала расчёта индекса цена акции А была равна 25 руб., 5-30 руб., С-55 руб. Количество выпущенных акций компании А составляло 200 штук, В — 300 штук и С — 400 штук. В момент времени Т цены акций составили: А 32 руб., В — 45 руб., С-44 руб., а количество выпущенных акций: А — 250 штук, В — 380 штук, С 400 штук. Значение индекса в момент начала его расчёта равно 10. Определить значение индекса в момент времени Т.

1. Определим значение индекса в момент времени Т

32*250+45*380+44*400 / 25*200+30*300+55*400 = 1,18611

Чистая цена облигации с фиксированным купоном равна 894,40 рублей. Выплаты купонов производятся 1 раз в год, годовой купонный доход равен 280 рублей. Какую полную цену рублях должен заплатить покупатель облигации (не считая комиссионных выплат брокеру), если со времени выплаты последнего купона прошло 78 дней? База: 365 дней в году.

1. Купон 280*78*365=59,8356

2. Цена 894,40+59,8356 = 954,24

Чистая цена облигации с фиксированным купоном равна 254,56 рублей. Выплаты купонов производятся 2 раз в год, годовой купонный доход равен 25 рублей. Какую полную цену в рублях должен заплатить покупатель облигации (не считая комиссионных выплат брокеру), если со времени выплаты последнего купона прошло 103 дня? База: 360 дней в году.

2. Цена 254,56+7,1523= 261,71

Чистая цена облигации с фиксированным купоном равна 456,34 рублей. Выплаты купонов производятся 4 раза в год, годовой купонный доход равен 50 рублей. Какую полную цену в рублях должен заплатить покупатель облигации (не считая комиссионных выплат брокеру), если со времени выплаты последнего купона прошло 56 дней? База: 360 дней в году.

1.Купон 50/4=12,5 12,5*56/90=7,77777

2. Цена 456,34+7,7777= 464,12

Чистая цена облигации с фиксированным купоном равна 103,45 рублей. Выплаты купонов производятся 2 раза в год, годовой купонный доход равен 10 рублей, купонный период 1 84 дня. Какую полную цену в рублях должен заплатить покупатель облигации (не считая комиссионных выплат брокеру), если со времени выплаты последнего купона прошло 143 дня?

1. Купон 10*6/12=5 5*143/184=3,89

Чистая цена облигации с фиксированным купоном равна 256,34 рублей. Выплаты купонов производятся 4 раза в год, годовой купонный доход равен 20 рублей, купонный период 91 день. Какую полную цену в рублях должен заплатить покупатель облигации (не считая комиссионных выплат брокеру), если со времени выплаты последнего купона прошло 34 дня?

1. Купон 20*3/12=5 5*34/91=1,87

Стоимость одной обыкновенной акций (вместе с накопленным дивидендом) компании к концу года составила 138 руб. В последние несколько лет предприятие работало стабильно и всю чистую прибыль распределяло в виде дивидендов по обыкновенным акциям; рентабельность активов RОА составила 24,5%. Владельцы акций в течение последних несколько лет получали стабильный доход по дивидендам в размере 18 руб. (дивиденды выплачивались один раз в конце года). Совет директоров одобрил проект реконструкции оборудования. При этом, согласно мнению финансовых аналитиков, проект замещения оборудования не должен приводить к дополнительным рискам. На собрании акционеров было решено не выплачивать дивидендов в конце этого года и проводить инвестиционный проект с начала нового года за счёт нераспределённой прибыли (невыплаченных дивидендов). Решено также, что в оставшиеся годы вся чистая прибыль будет выплачиваться в виде дивидендов. Чему станет равна теоретическая стоимость (в рублях) акций компании в результате реорганизации?

1. Теоретическая стоимость акции

стоимость одной обыкновенной акции (вместе с накопленным дивидендом) компании к концу года составила 250 рублей. В последние несколько лет предприятие работало стабильно и всю чистую прибыль распределяла в виде дивидендов по обыкновенным акциям. Дивидендная доходность по акциям в течение последних несколько лет была стабильна составляла 22% годовых. Совет директоров одобрил проект реконструкции оборудования. При этом, согласно мнению финансовых аналитиков, проект замещения оборудования не должен приводить к дополнительным рискам. Рентабельность активов (RОА) предприятия в последние несколько лет была стабильной величиной и составляла 27% за год. На собрании акционеров было решено не выплачивать дивидендов в конце этого года и проводить инвестиционный проект с начала нового года за счёт нераспределённой прибыли (невыплаченных дивидендов). Чему станет равна теоретическая стоимость (в рублях) акций компании в результате реорганизации?

1. Теоретическая стоимость акции

Стоимость одной обыкновенной акции (вместе с накопленным дивидендом) компании к концу года составила 115 руб. В последние несколько лет предприятие работало стабильно и всю чистую прибыль распределяло в виде дивидендов по обыкновенным акциям. Владельцы акций в течение последних несколько лет получали стабильный доход по дивидендам в размере 15 руб. (дивиденды выплачивались один раз в конце года). Совет директоров одобрил проект реконструкции оборудования. При этом, согласно мнению финансовых аналитиков, проект замещения оборудования не должен приводить к дополнительным рискам, а внутренняя норма доходности проекта IRR составляет 22,4%. На собрании акционеров было решено не выплачивать дивидендов в конце этого года и проводить инвестиционный проект с начала нового года за счёт нераспределённой прибыли (невыплаченных дивидендов). Чему станет равна теоретическая стоимость (в рублях) акций компании в результате реорганизации.

1. Теоретическая стоимость акции в рублях (115-15) * 1,224 = 122,4

Стоимость одной обыкновенной акции (вместе с накопленным дивидендом) компании к концу года составила 215 руб. В последние несколько лет предприятие работало стабильно и всю чистую прибыль распределяло в виде дивидендов по обыкновенным акциям. Дивидендная доходность акций 19,4% годовых. Совет директоров одобрил проект реконструкции оборудования. Согласно мнению финансовых аналитиков, проект замещения оборудования не должен приводить к дополнительным рискам, а внутренняя норма доходности проекта IRR составляет 24,5%. На собрании акционеров было решено не выплачивать дивидендов в конце этого года и проводить инвестиционный проект с начала нового года за счёт нераспределённой прибыли (невыплаченных дивидендов). Чему станет равна теоретическая стоимость (в рублях) акций компании в результате реорганизации.

1. Теоретическая цена акции 1,245*215 / 1,194 = 224,18

Привилегированная акция приносит ежемесячный доход 360 руб. Рыночная цена акции – 16280 руб. Найти доходность акции (номинальную процентную ставку при начислении процентов 12 раз в год), считая что дивиденды по ней не будут меняться и будут выплачиваться достаточно долго.

При прогнозировании инвестиционного проекта было посчитано, что на каждые 6000 $ затрат доходы по годам распределятся следующим образом: 2800$ в конце первого года, 3600$ в конце второго года, 4500$ в конце третьего года. Определить внутреннюю норму прибыли проекта.

1. IRR лучше подставить как неизвестное в обычную формулу.

2800 / (1+IRR)^1 + 3600/(1+IRR)^2 + 4500/(1+IRR)^3 = 6000

Вам предлагают бескупонную облигацию, которая будет погашена через 6 лет по номиналу 7500 руб. По какой цене Вы её приобретёте, если банковская депозитная ставка на тот же срок равна 23 % годовых, риск инвестиций предлагается учесть с помощью премии за риск в размере 3,5% годовых.

1. Цена 7500/(1+0,23+0,035)^6= 1830.28

Найти ставку размещения бескупонной облигации, если рыночная цена на настоящий момент равна 850 руб. Облигация погашается по номиналу 1200 руб. через 2 года и 2 месяца.

1. Ставка размещения

При прогнозировании инвестиционного проекта было посчитано, что на каждые 2000 рублей затрат чистые доходы по годам распределятся следующим образом: 500 руб. в конце I года, 670 руб. – в конце II года, 885 руб. — в конце III года, 460 руб. — в конце IV года, 230 руб. — в конце V года. Рассчитать внутреннюю норму прибыли проекта.

1. Внутренняя норма прибыли (определяем подстановкой)

500/(1+X)^1 + 670/(1+X)^2 + 885/(1+X)^3 + 460/(1+X)^4 + 230/(1+X)^5 = 2000

Найти ставку размещения бескупонной облигации, если рыночная цена на настоящий момент равна 2860 руб. Облигация погашается по номиналу 3500 руб. через 1 года и 4 месяца.

1. Ставка размещения

Сравниваются 2 инвестиционных проекта, имеющие следующие денежные потоки (тыс. руб.)

При каком значении ставки дисконтирования оба проекта будут иметь одинаковое значение чистой приведённой стоимости NPV

1. (определяем подстановкой из ответов)

(-400-(-370))/(1+I)^1 + (200-50)/(1+I)^2 + (100-120)/(1+I)^3 + (60-210)/(1+I)^4 = 0.00

9.1.87
Чистая цена облигации с фиксированным купоном равна 456,34 рублей. Выплаты купонов производятся 4 раза в год, годовой купонный доход равен 50 рублей. Какую полную цену в рублях должен заплатить покупатель облигации (не считая комиссионных выплат брокеру), если со времени выплаты последнего купона прошло 56 дней? База: 360 дней в году.

К чистой цене прибавляем накопленный купонный доход (с момента выплаты последнего купона)
P = 456,34 + (50/4) х 56/(360/4) = 464,12 руб .

11.1.4
Для формирования портфеля инвестор использовал собственные средства и также получил кредит сроком на год в размере 300 тыс. руб. под 9% годовых. Инвестор приобрёл акции двух видов: акции А на сумму 400 тыс. руб. с ожидаемой доходностью 20,6% и акции В на сумму 600 тыс. руб. с ожидаемой доходностью 28,5%. Определить ожидаемую доходность портфеля инвестора за год.

1. Определяем сумму дохода

r _p = 400 х 20,6% + 600 х 28,5% – 300 х 9% = 226,4

2. Делим доход на затраты

226,4 / 700 (сумма затрат) = 0,3234

Определить риск портфеля, состоящего из акций А и В, если доля акции А в портфеле составляет 30%, стандартное отклонение доходности акции А за период равно 15%, акции В: 45%. Коэффициент ковариации доходностей равен 150.

Решение
σР = (0,32х152 + (1-0,3) 2 х452 + 2х0,3х(1-0,3)х150) 1/2 = 32,79%

Определить риск портфеля, состоящего из акций А и В, если доля акции А в портфеле составляет 30%, стандартное отклонение доходности акции А за период равно 15%, акции В: 45%. Коэффициент корреляции доходностей равен 1.

σ _Р = (0,3 2 х15 2 + (1-0,3) 2 х45 2 + 2х0,3х(1-0,3)х15х45х1) 1/2 = 36%

Пусть распределение вероятности доходности некоторого актива за один период выглядит следующим образом

Источник