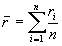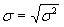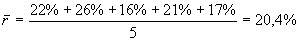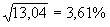Пример 5
Доходность актива за 8 лет представлена в таблице.
| Годы | ||
| Доходность, % | -10 | -5 |
Определите риск данного актива, используя показатели выборочной дисперсии и стандартного отклонения.
Выборочная дисперсия доходности актива определяется по формуле
где 


На основании имеющихся данных рассчитаем среднюю доходность актива:

Теперь рассчитаем выборочную дисперсию доходности актива:

+ (–5 – 8) 2 + (6 – 8) 2 + (15 – 8) 2 ]/8 = 93,75 %.
Стандартное отклонение доходности определяется как корень квадратный из дисперсии:
Таким образом, выборочное стандартное отклонение доходности равно:
Стандартное отклонение показывает степень риска НЕнас-тупления запланированной доходности.
ЗАДАНИЕ
Выполнение группой (до3 человек) одного из нижеприведенных заданий, в которых предлагается провести анализ некоторых вопросов по определенной теме и выбрать выгодный вариант инвестирования.
Дата добавления: 2015-04-11 ; просмотров: 3 | Нарушение авторских прав
Источник
Доходность актива представлена за 8 лет определить риск актива
Ребята,
Очень прошу помочь с решением задач для базового экзамена! Мне очень нужно срочно!
Буду очень признательна. У меня есть все конспекты и вопросы и т.д., но нет решения всех задач, особенно со случайными величинами, корреляцией и матожиданиями. Очень буду признательна, ребята. Спасибо заранее!
Этот e-mail адрес защищен от спам-ботов, для его просмотра у Вас должен быть включен Javascript
Re: Решение задач по базовому экзамену 12.02.2013 22:58 #1075
|
| Дата | Закрытие | ln | |
| 31.03.2010 | 1572,48 | 1,006522 | 0,006501 |
| 30.03.2010 | 1562,29 | 1,006909 | 0,006885 |
| 29.03.2010 | 1551,57 | 1,020857 | 0,020643 |
| 26.03.2010 | 1519,87 | 1,003188 | 0,003183 |
| 25.03.2010 | 1515,04 | 1,000304 | 0,000304 |
| 24.03.2010 | 1514,58 | 0,993193 | -0,00683 |
| 23.03.2010 | 1524,96 | 0,999587 | -0,00041 |
| 22.03.2010 | 1525,59 | 0,987622 | -0,01245 |
| 19.03.2010 | 1544,71 | 0,990961 | -0,00908 |
| 18.03.2010 | 1558,8 | 0,997019 | -0,00299 |
| 17.03.2010 | 1563,46 | 1,017354 | 0,017205 |
| 16.03.2010 | 1536,79 | 1,014785 | 0,014677 |
| 15.03.2010 | 1514,4 | 0,986786 | -0,0133 |
| 12.03.2010 | 1534,68 | 1,020372 | 0,020167 |
| 11.03.2010 | 1504,04 | 1,001758 | 0,001757 |
| 10.03.2010 | 1501,4 | 0,999135 | -0,00087 |
| 09.03.2010 | 1502,7 | 0,996347 | -0,00366 |
| 05.03.2010 | 1508,21 | 1,025707 | 0,025382 |
| 04.03.2010 | 1470,41 | 1,006992 | 0,006968 |
| 03.03.2010 | 1460,2 | 1,010086 | 0,010035 |
| 02.03.2010 | 1445,62 |
Скользящая средняя равна 0,004206.
Шаг 4. Найдите 20-дневную дисперсию выборки данных из шага 2. Для этого необходима 20-дневная скользящая средняя (см. шаг 3). Далее, для каждого из 20 последних дней вычтем скользящую среднюю из значений шага 2.
Теперь возведем в квадрат полученные значения, чтобы преобразовать все отрицательные ответы в положительные. После этого сложим все значения за последние 20 дней. Наконец, разделим найденную сумму на 19 и получим дисперсию по выборке данных за последние 20 дней. 20-дневная дисперсия для 100303 составляет 0,00012481.
Шаг 5. После того как вы определили 20-дневную дисперсию для конкретного дня, необходимо преобразовать ее в 20-дневное стандартное отклонение. Это легко сделать путем извлечения квадратного корня из дисперсии. Таким образом, для 100303 квадратный корень дисперсии даст нам 20-дневное стандартное отклонение 0,01117183.
Шаг 6. Теперь преобразуем полученные данные в «годовые». Так как мы используем дневные данные и исходим из того, что по РТС в году 252 торговых дня (примерно), умножим ответы из шага 5 на квадратный корень 252, то есть на 15,87450787. Для 100303 20-дневное стандартное отклонение по выборке составляет 0,01117183. Умножив его на 15,87450787, получаем 0,177347308. Это значение является исторической волатильностью, в нашем случае — 17,73%.
Пример расчета коэффициентов бета, альфа и Шарпа:
Бета показывает уровень риска ПИФа в сравнении с индексом. Например, значение 0,5 говорит о том, что растет и падает ПИФ на половину меньше, чем индекс (индекс вырос +1% — ПИФ вырос +0,5%, индекс упал на 2% — ПИФ упал на 1%). С бетой = 2 ПИФ удваивал бы любое колебание индекса.
Альфа показывает превышение доходности (вследствие мастерства управления) ПИФа над доходностью индекса (доходность индекса корректируется на бету ПИФа для этого сравнения). Например, если бета = 1 («ноздря в ноздрю», индексный ПИФ), то альфа равная 0,4 означает, что ПИФ переиграл индекс на 0,4%. При бета 0,5 альфа 0,4 говорит о том, что ПИФ показал доходность равную половине доходности индекса плюс 0,4%.
Коэффициент Шарпа показывает доходность, полученную на одну условную единицу риска. Риск ПИФов всех категорий измеряется в универсальных условных единицах (стандартное отклонение). Доходность для расчета коэффициента Шарпа берется только та, что получается с риском. Для этого из реальной доходности ПИФа вычитается доходность безрискового актива — депозита в Сбербанке. Оставшаяся доходность делится на количество «потраченных» на её получение единиц риска. С помощью этого коэффициента можно сравнить мастерство управления ПИФами как одной, так и разных категорий: если ПИФ облигаций на каждую из немногих единиц риска получил большую доходность, чем ПИФ акций на каждую из единиц риска, которых у него больше, то ПИФ облигаций управляется лучше, хотя он получает меньшую суммарную доходность.
Для расчета коэффициента (помимо ежедневной стоимости пая) необходимо выбрать:
— безрисковый актив — актив, доходность по которому заранее известна и риски, связанные с получением этой доходности малы, а период обращения данного актива равен (или близок) периоду, за который проводится оценка. В качестве безрискового актива берется двухгодовой вклад в рублях Сбербанка России — «Накопительный».
— параметр сглаживания — позволяет наиболее точно отразить субъективную временную оценку наблюдений, т. е. снизить влияние наблюдений за деятельностью компаний, произведенных достаточно давно. Принимает значения от 0 до 1. Предлагается положить его, традиционно, равным 0.94.
От величины коэффициента сглаживания зависит то, как сильно будет сглажено влияние на результат более отдаленных наблюдений по отношению к менее отдаленным. Т.е., чем ближе коэффициент к 0, тем меньшее влияние отдаленных наблюдений. И наоборот: чем ближе коэффициент к 1, тем больше влияние отдаленных наблюдений.
Методики расчета коэффициента Шарпа:
Допустим, у нас есть кривая эквити (текущая прибыль или убыток по открытым позициям +/- своп. Своп (Swap) – одновременная продажа и покупка одного количества определенной валюты с разными датами валютирования. Обычно, свопирование производится при переносе открытой позиции на следующий день. Свопировать открытую валютную позицию – означает сохранить состояние позиции (размер и знак) на определенный срок в будущем) за несколько месяцев. Доходность за конкретный месяц определяется по формуле:
Pn – доходность за n-ный месяц.
Eo – эквити на момент открытия месяца.
Ec – эквити на момент закрытия месяца,
Имея эквити, мы можем получить набор доходностей по месяцам. Пусть, для примера, набор будет таким:
| период | доходность за месяц | ||
| 23.04-22.05 | 1,270739798 | 0,198718571 | 0,03948907 |
| 22.05-22.06 | 0,771721484 | -0,300299743 | 0,09017994 |
| 22.06-22.07 | 1,118099988 | 0,04607876 | 0,00212325 |
| 22.07-21.08 | 1,137465906 | 0,065444679 | 0,00428301 |
| 21.08-21.09 | 1,078794388 | 0,006773161 | 4,5876E-05 |
| 21.09-21.10 | 1,183038115 | 0,111016888 | 0,01232475 |
| 21.10-20.11 | 0,958390154 | -0,113631074 | 0,01291202 |
| 20.11-18.12 | 1,015705304 | -0,056315923 | 0,00317148 |
| 18.12-18.01 | 1,203006763 | 0,130985536 | 0,01715721 |
| 18.01-18.02 | 0,917570058 | -0,154451169 | 0,02385516 |
| 18.02-18.03 | 1,081313618 | 0,009292391 | 8,6349E-05 |
| 18.03-16.04 | 1,12840915 | 0,056387923 | 0,0031796 |
Можно также в качестве набора доходностей использовать прибыли по сделкам – не обязательно чтобы доходность считалась именно по месяцам. Однако общепринятым способом является вычисление Шарпа по набору месячных доходностей.
Определим матожидание (средний уровень ряда):
Рассчитаем дисперсию (таблица выше).
Рассчитаем стандартное отклонение:
Вычисление коэффициента Шарпа основано на формуле:
Существует 3 варианта расчета коэффициента Шарпа:
1. The Sharpe Ratio. William F. Sharpe. Stanford University. 1994.
В этом случае исходный массив подвергается простому преобразованию: из него вычитается безрисковая ставка. Затем применяется основная формула.
Вклад «Накопительный» Сбербанка России предлагает ставку 5,75% годовых на период до 1 года (сумма вклада от 30000 до 100000 руб.).
Вычислим превышение доходности над безрисковой ставкой:
| доходность за месяц | безрисковая ставка | превышение |
| 1,270739798 | 0,479166667 | 0,791573131 |
| 0,771721484 | 0,479166667 | 0,292554817 |
| 1,118099988 | 0,479166667 | 0,638933321 |
| 1,137465906 | 0,479166667 | 0,658299239 |
| 1,078794388 | 0,479166667 | 0,599627721 |
| 1,183038115 | 0,479166667 | 0,703871448 |
| 0,958390154 | 0,479166667 | 0,479223487 |
| 1,015705304 | 0,479166667 | 0,536538637 |
| 1,203006763 | 0,479166667 | 0,723840096 |
| 0,917570058 | 0,479166667 | 0,438403392 |
| 1,081313618 | 0,479166667 | 0,602146951 |
| 1,12840915 | 0,479166667 | 0,649242484 |
Находим матожидание и стандартное отклонение:
Тогда коэффициент Шарпа:
S=4,494335804.
2. Modified Sharpe Ratio.
Находим матожидание и стандартное отклонение набора доходностей.
Пересчитываем доходность на год, для чего матожидание E умножаем на число периодов в году:
Eгод = 1,072021227 * 12 = 12,86425472.
Вычисляем превышение прибыли над безрисковой ставкой, по формуле:
Превышение прибыли = Eгод – безрисковая ставка
Превышение прибыли = 12,86425472 – 5,75 = 7,114254724.
Стандратное отклонение тоже пересчитываем на год, по формуле:
σгод = 0,1319115 * 3,464 = 0,456954827.
Вычисляем коэффициент Шарпа:
S = Превышение прибыли / σгод = 3,250893038.
3. Annual Sharpe Ratio.
Рассматриваем значения счета и доходность по месяцам.
| период | доходность за месяц | Закрытие |
| 23.04-22.05 | 1,270739798 | 3424,72 |
| 22.05-22.06 | 0,771721484 | 2642,93 |
| 22.06-22.07 | 1,118099988 | 2955,06 |
| 22.07-21.08 | 1,137465906 | 3361,28 |
| 21.08-21.09 | 1,078794388 | 3626,13 |
| 21.09-21.10 | 1,183038115 | 4289,85 |
| 21.10-20.11 | 0,958390154 | 4111,35 |
| 20.11-18.12 | 1,015705304 | 4175,92 |
| 18.12-18.01 | 1,203006763 | 5023,66 |
| 18.01-18.02 | 0,917570058 | 4609,56 |
| 18.02-18.03 | 1,081313618 | 4984,38 |
| 18.03-16.04 | 1,12840915 | 5624,42 |
Первое значение эквити обозначим как FirstClose, последнее – LastClose.
Находим количество дней между FirstClose и LastClosе. Оно равно 226. Находим долю этого периода в году: 226/365 = 0,619178082.
Пересчитываем доходность на год по формуле:
G = (LastClose/FirstClose)^(1/YearPart) — 1
G = (5624,42 / 3424,72)^(1/0,619178082) – 1 = 1,228258653.
Вычисляем превышение над безрисковой ставкой:
GE = G — RiskFreeRate
GE = 1,228258653 — 0.0575 = 1,170758653.
Теперь надо вычислить стандартное отклонение, получаем:
Пересчитываем стандартное отклонение за год:
σгод = 0,1319115 * 3,464 = 0,456954827.
Источник




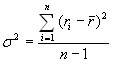 ,
,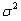 – дисперсия доходности актива;
– дисперсия доходности актива;