Доходность актива имеет нормальное распределение

Распределение доходностей на рынке акций

Автор: Дмитрий Никитенко
Дата записи

Сегодня мы разберем очень интересную тему о распределении доходностей акций. Она раскрывает природу инвестиционного риска ещё глубже и позволяет лучше понять как именно работает фондовый рынок и чего от него следует ожидать.

Если вы ещё не читали статью про инвестиционный риск, стоит сначала прочитать в ней про стандартное отклонение.

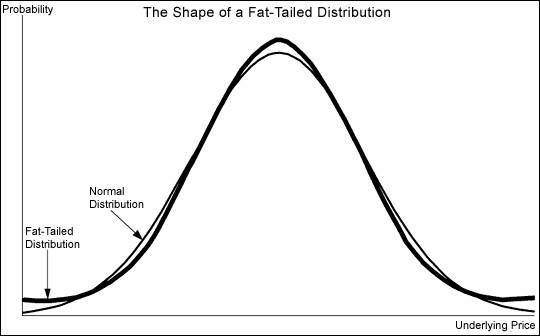
Распределение доходностей на фондовых рынках принято сравнивать с кривой нормального распределения (по функции Гаусса). Хотя далее мы выясним, что реальное распределение доходностей не полностью соответствует этой кривой, она весьма неплохо описывает происходящее на рынке на длинных периодах времени.

Кривая нормального распределения. По оси X – стандартное отклонение, по оси Y – вероятность. Проценты – это частота попадания значения стандартного отклонения в закрашенную область под кривой. Источник: Википедия

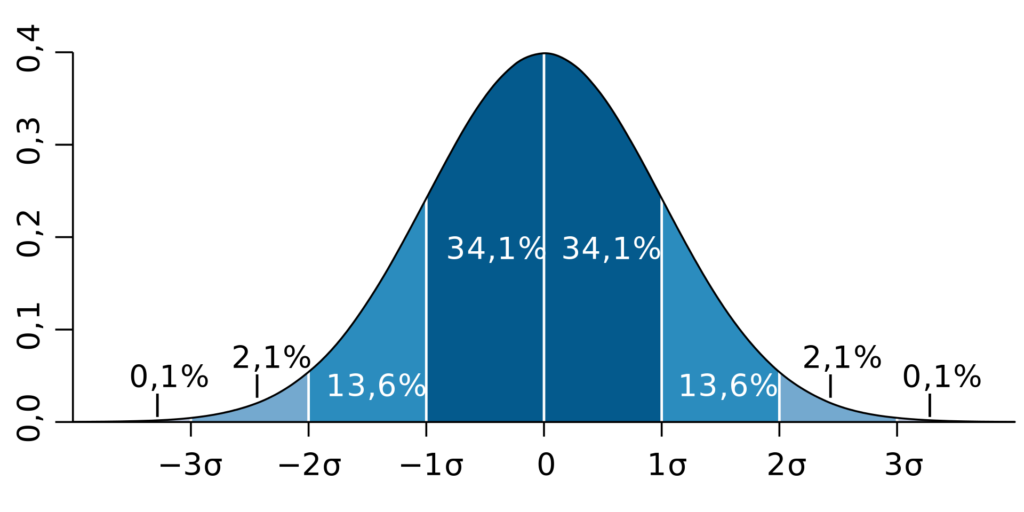
Смысл нормального распределения заключается в том, что основная часть значений случайной величины концентрируется возле своей средней (математического ожидания случайной величины), а значения по краям кривой маловероятны (случаются редко). Так, чем больше стандартное отклонение значений от среднего, тем меньше вероятность их появления.

В статистике существует правило трёх сигм (стандартных отклонений), которое наглядно изображено на графике выше. Закрашенные на нём области под кривой показывают сколько процентов времени стандартное отклонение значений случайной величины не превышает одну, две или три сигмы. Значения с отклонением более трёх сигм считаются практически невозможными.

Чтобы проверить соблюдается ли нормальное распределение доходностей на рынке акций, возьмем полные (с дивидендами) реальные (выше инфляции) доходности акций США на периоде с 1871 по 2018 год (по данным Роберта Шиллера и Yahoo! Finance):

• среднее арифметическое этих доходностей составило 8.5%;
• стандартное отклонение = 18.5%.

Если бы кривая нормального распределения полностью описывала распределение доходностей на фондовом рынке, то, согласно правилу трёх сигм:

• 68.27% времени доходность была бы между средним арифметическим ± одно стандартное отклонение (-10% и 27%);
• 95.45% времени – между средним ± два стандартных отклонения (-28.5% и 45.5%);
• 99.73% времени – между средним ± три стандартных отклонения (-47% и 64%).

Наблюдение за реальными данными даёт хоть и похожий, но всё же отличающийся результат. На самом деле доходности рынка акций США выше инфляции за 148 лет укладывались:

• в одно стандартное отклонение от своей средней арифметической 67.57% времени (не 68.27%);
• в два стандартных отклонения – 93.92% времени (не 95.45%);
• в три стандартных отклонения – 100% времени (не 99.7%), значений за пределами -47% и 64% за этот период не было, минимальная и максимальная доходность составили -38.47% в 1931 году и 57.16% в 1954 году.

Получается, что 9 из 148 лет принесли доходность меньше -28.49% или больше 45.51% (двух стандартных отклонений), что составило 6.08% случаев, а не ожидаемые согласно нормальному распределению 100% — 95.45% = 4.55%. Разница не так велика, но она есть и говорит о том, что аномальные доходности на рынке акций немного более вероятны, чем предсказывает нормальное распределение.

Посмотрим на те же данные по США на графике распределения доходностей. Здесь и далее снова используются полные реальные годовые доходности, разделенные на интервалы по 10%, каждый год определен в свой интервал.

Источники данных: Robert Shiller, Yahoo! Finance; инфляция: Robert Shiller, Bureau of Labor Statistics

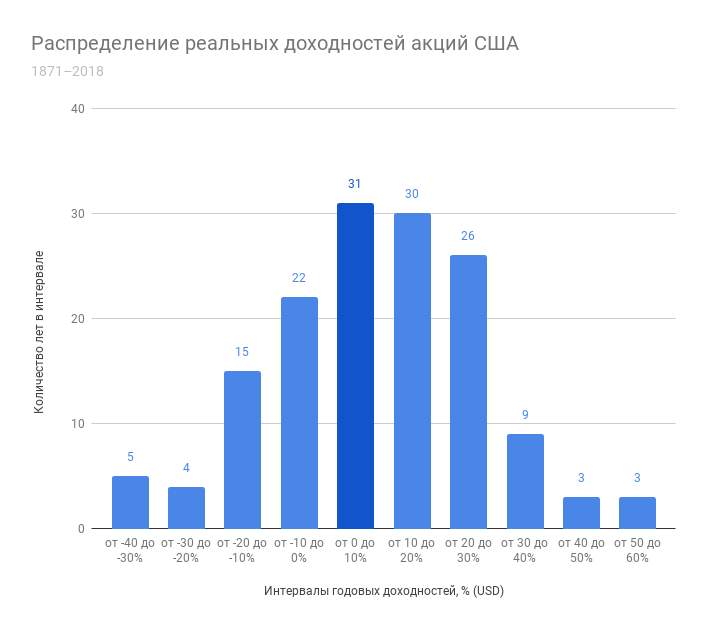
График напоминает кривую нормального распределения, однако, крайних значений немного больше, чем предполагает гауссиана, а значит они случаются чаще. Интервал от -40 до -30% содержит в себе 5 лет, что больше, чем у предыдущего интервала от -30 до -20% (4 года), а интервал от 50 до 60% содержит в себе столько же лет (3), сколько и предыдущий, хотя согласно нормальному распределению тоже должен быть меньше.

Это называется fat tail или толстый хвост кривой – вместо того, чтобы стремиться к оси абсцисс (к нулю), кривая может отрываться от неё, что не соответствует нормальному распределению. Крупные просадки или аномально высокие доходности не настолько маловероятны как предсказывает гауссиана, что получило название tail risk. Такое поведение рынка подчёркивает важность психологии в инвестировании и умения инвестора пережидать плохие годы, не продавая активы. Каким бы плохим не был отдельно взятый день или год, доходность акций и облигаций имеет положительное математическое ожидание (среднее значение), а значит время и сложный процент сделают своё дело.

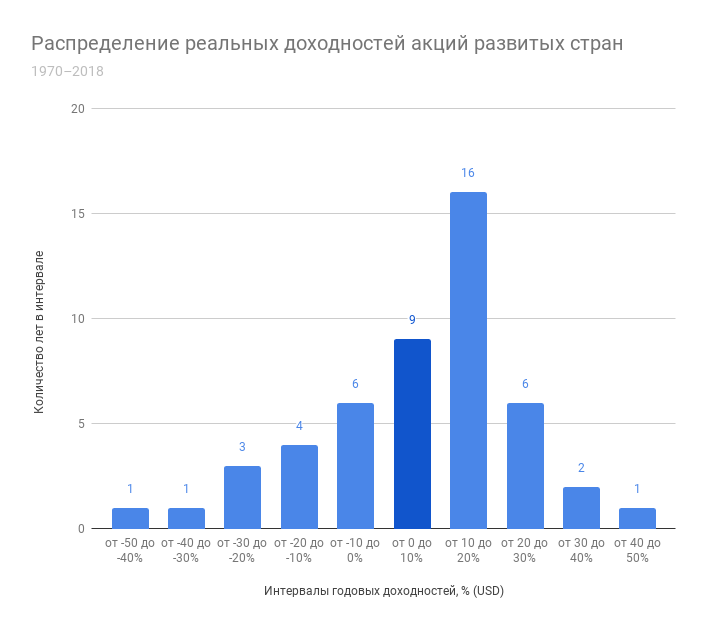
Используя индекс полной доходности MSCI World Net я также построил график распределения реальных годовых доходностей акций развитых стран. Хотя доступная выборка по нему значительно меньше (с 1970 года), можно отметить сходство в количестве положительных периодов с акциями США – практически 70% времени он приносил положительную реальную доходность. Об особенностях распределения на этом периоде я говорить не буду – довольно маленькое число наблюдений. Здесь худшим годом для индекса стал 2008 – доходность едва опустилась за -40% с учетом инфляции, а лучшим – 1986 с практически такой же доходностью, но без минуса.

График: Capital-Gain.ru. Источники данных: MSCI World Net Index; инфляция: Bureau of Labor Statistics

И, наконец, давайте посмотрим на распределение месячных доходностей на рынке акций США с 1988 года (375 месяцев).

График: Capital-Gain.ru. Источник данных: Yahoo! Finance

Здесь тоже можно заметить аномальные доходности по краям (больше ±10% за один месяц — это сильно). Но что ещё общего можно заметить на этих графиках? Они все немного сдвинуты вправо по оси доходностей, можно сказать, имеют больший вес в своей положительной части. Это является свидетельством того, что доходность акций исторически имела положительное математическое ожидание. По сути мы видим здесь ту добавленную стоимость, что генерирует бизнес по всему миру.

Нассим Николас Талеб в своей книге «Черный лебедь» пишет, что нормальное распределение отлично подходит для описания физически ограниченных значений (например, рост человека), потому что они не масштабируются так сильно, как физически неограниченные (например, продажи бестселлера или доходность фондового рынка). Конечно, ни продажи, ни доходность не могут быть бесконечными, однако, вы с гораздо меньшей вероятностью встретите человека ростом 3 метра, чем неожиданно проданную огромным тиражом книгу или аномальную доходность на рынке. Такие из ряда вон выходящие события он называет черными и белыми лебедями (в зависимости от того негативный оно имеет смысл или позитивный). Тут стоит отметить, что, на мой взгляд и по результатам самостоятельного анализа данных, как нормальное распределение не описывает доходности на фондовом рынке полностью, так и Талеб в своей книге преувеличивает значимость этих отклонений от нормального распределения , если смотреть на них с точки зрения долгосрочного инвестора. Для трейдеров, впрочем, эти отклонения действительно могут быть гораздо более значительными, ведь они оперируют более короткими временными интервалами, на которых аномальные (для правила трёх сигм) доходности случаются чаще – в дневных и месячных данных появляются стандартные отклонения и больше трёх сигм, что по нормальному распределению практически невозможно. К тому же трейдеры могут автоматически фиксировать убытки с помощью биржевых заявок стоп лосс, которые не применяются пассивными портфельными инвесторами.

Популярным примером является черный понедельник 19 октября 1987 года, когда индекс Dow Jones за один день упал на 22.61% – 25 своих дневных стандартных отклонений (!). Более недавний пример, изображенный на графике ниже – 24 июня 2016 года, когда состоялся референдум о Брексите и некоторые активы продемонстрировали аномальную дневную доходность. Количество лет в последней колонке таблицы, которые, согласно нормальному распределению, надо подождать, чтобы увидеть такие дневные доходности, намекает нам, что они гораздо более вероятны, чем может предсказать кривая Гаусса.

Доходности инструментов в день референдума в Великобритании, их множитель СКО и количество лет, раз в которые они ожидаются согласно нормальному распределению вероятностей. Источник: Charlie Bilello

Несмотря на то, что аномальные доходности на фондовом рынке – не такая редкость, как может спрогнозировать кривая нормального распределения, долгосрочному инвестору не стоит обращать внимания на них и уж тем более продавать свои активы из-за плохих новостей, фиксируя убыток , потому что такие аномальные доходности встречаются чаще именно на дневных или месячных данных, чем на годовых. Картинка ниже вполне подтверждает выделенные в этой статье утверждения – плохие новости или нет, положительная ожидаемая доходность и сложный процент долгосрочно заставляют капитал расти.

Прирост капитала, вложенного в акции компаний малой капитализации (small stocks), крупной капитализации (large stocks), государственные облигации (government bonds), векселя (treasury bills) и инфляция. Источник: SeekingAlpha

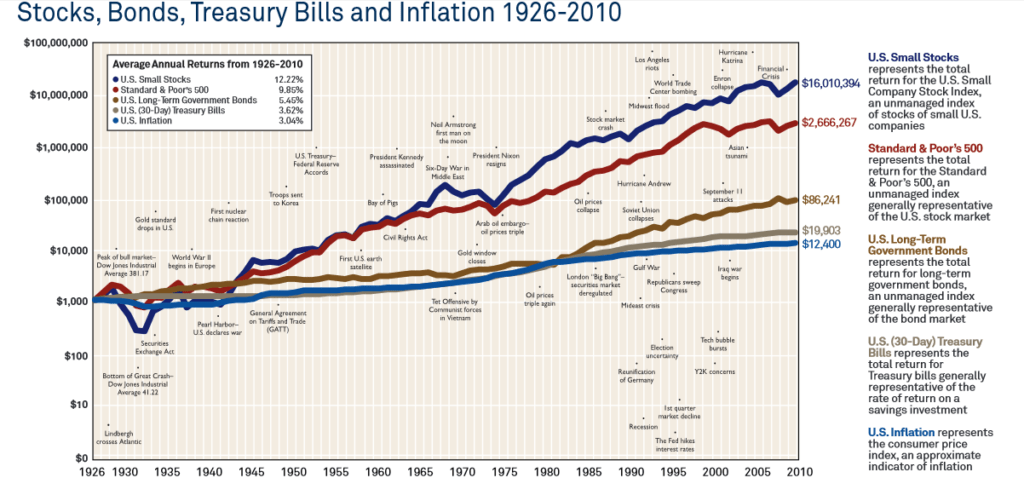
На выше графике показаны события, которые повлияли на рынок. Как видите, несмотря на войны и кризисы, активы показали значимый прирост капитала, опережающий инфляцию. Другой популярный пример против торговли по новостям показывает, как часто СМИ ошибаются в своих прогнозах.

График индекса акций США S&P 500 и новостные заголовки. Источник: Barry Ritholtz

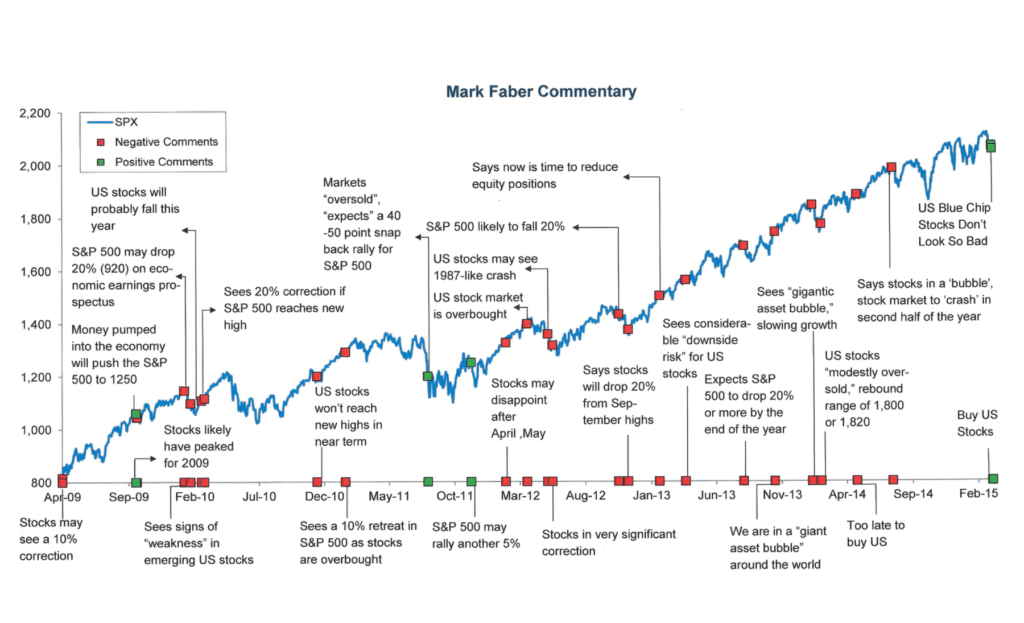
Комиссии и распределение доходностей

На новости мы повлиять не можем, зато вполне возможно повлиять на комиссии и налоги, которые инвестор платит фондам, брокерам и государству. Чем больше размер комиссий и налогов, тем меньше математическое ожидание доходности портфеля, а значит и распределение его доходностей на графике смещается влево на размер комиссий и налогов – ближе к отрицательной зоне. Схематично это показано на графике ниже.

Влияние комиссий и налогов на распределение доходностей. Источник: Vanguard

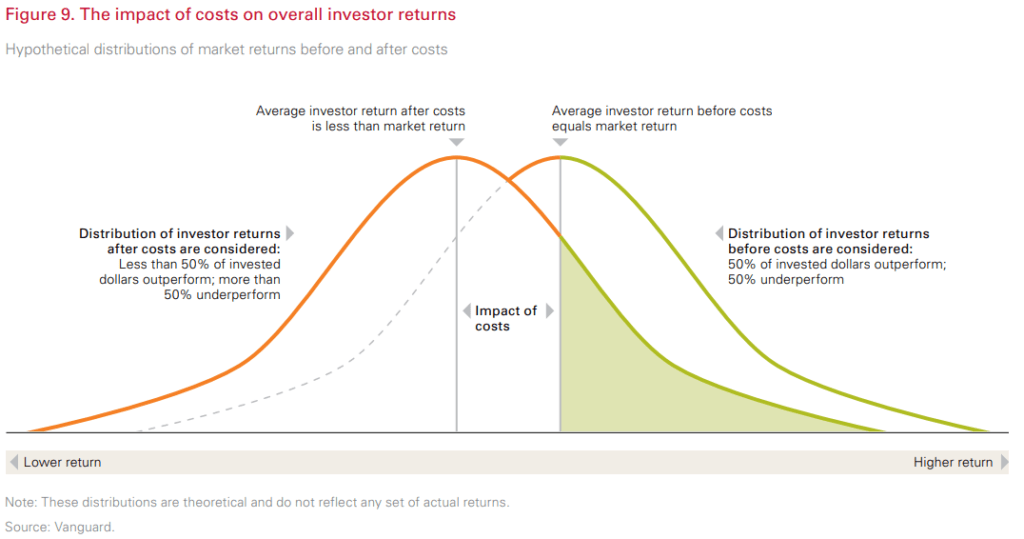
Долгосрочному пассивному инвестору гораздо полезнее думать о том как уменьшить свои комиссии и воспользоваться налоговыми льготами, чем о новостях и аномалиях на фондовом рынке.

Источник

Pokrovka11’s Blog

Почему распределение доходности считается нормальным? Статистика в финансах.

Одной из основных предпосылок в финансовой экономике является предположение о том, что доходности финансовых активов имеют нормальное распределение. Данное предположение существенно упрощает проблему выбора портфеля для инвестирования, так как позволяет сравнивать альтернативные портфели всего по двум критериям: стандартное отклонение и математическое ожидание. Подтверждение данной гипотезы очень важно для инвесторов (которые определяют риски вложения средств в портфели на основе распределения доходностей), а также финансовых экономистов (которые рассматривают распределение в качестве косвенной информации об экономических факторах, влияющих на доходности).

Однако подчиняются ли доходности финансовых активов нормальному распределению? «Отец финансов», Нобелевский лауреат Юджин Фама в своем дипломе показал, что распределение доходностей акций имеет толстые хвосты (Fama, “The behavior of stock market prices”, 1965b). Для инвесторов данная информация усложняет процесс определения риска вложения средств, ведь два портфеля могут иметь одинаковую доходность и стандартное отклонение, однако, вероятность отклонения от среднего у одного портфеля может быть выше. Для экономистов это означает, что экономические факторы, вызывающие доходность ценных бумаг, сами подвержены частым и внезапным потрясениям.

Здесь у читателя возникает логичный вопрос: а зачем тогда финансовые экономисты до сих пор используют предпосылку о нормальности распределения доходностей? Объяснение кроется в центральной предельной теореме (ЦПТ): если количество дней, за которое рассчитывается логарифм кумулятивной доходности, является большим, то распределение суммы логарифмов стремится к нормальному.

Благодаря ЦПТ финансовые экономисты сохраняют за собой право использовать предпосылку о нормальности распределения при переходе к логарифму кумулятивной доходности. Предпосылка о нормальности распределения дневных доходностей при этом объясняется лишь ее удобством.

Подробнее можно почитать в учебнике Fama “Foundations of Finance” (1976).

Источник

Нормальное распределение (Гаусса) в Excel

В статье подробно показано, что такое нормальный закон распределения случайной величины и как им пользоваться при решении практически задач.

Нормальное распределение в статистике

История закона насчитывает 300 лет. Первым открывателем стал Абрахам де Муавр, который придумал аппроксимацию биномиального распределения еще 1733 году. Через много лет Карл Фридрих Гаусс (1809 г.) и Пьер-Симон Лаплас (1812 г.) вывели математические функции.

Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение.

Нормальный закон не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. Конкретная форма распределения задается специальными параметрами. Например, у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами.

Кривая нормального распределения Гаусса имеет следующий вид.

График нормального распределения напоминает колокол, поэтому можно встретить название колоколообразная кривая. У графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.

На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.

Формула нормального распределения (плотности) следующая.

Формула состоит из двух математических констант:

π – число пи 3,142;

е – основание натурального логарифма 2,718;

двух изменяемых параметров, которые задают форму конкретной кривой:

m – математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);

ну и сама переменная x, для которой высчитывается плотность вероятности.

Конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии ( σ 2 ). Кратко обозначается N(m, σ 2 ) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ 2 характеризует размах вариации, то есть «размазанность» данных.

Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности.

А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса концентрируется у центра. Если же у данных большой разброс, то они «размазываются» по широкому диапазону.

Плотность распределения не имеет прямого практического применения. Для расчета вероятностей нужно проинтегрировать функцию плотности.

Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:

Используя математические свойства любого непрерывного распределения, несложно рассчитать и любые другие вероятности, так как

P(a ≤ X 0 =1 и остается рассчитать только соотношение 1 на корень из 2 пи.

Таким образом, по графику хорошо видно, что значения, имеющие маленькие отклонения от средней, выпадают чаще других, а те, которые сильно отдалены от центра, встречаются значительно реже. Шкала оси абсцисс измеряется в стандартных отклонениях, что позволяет отвязаться от единиц измерения и получить универсальную структуру нормального распределения. Кривая Гаусса для нормированных данных отлично демонстрирует и другие свойства нормального распределения. Например, что оно является симметричным относительно оси ординат. В пределах ±1σ от средней арифметической сконцентрирована большая часть всех значений (прикидываем пока на глазок). В пределах ±2σ находятся большинство данных. В пределах ±3σ находятся почти все данные. Последнее свойство широко известно под названием правило трех сигм для нормального распределения.

Функция стандартного нормального распределения позволяет рассчитывать вероятности.

Понятное дело, вручную никто не считает. Все подсчитано и размещено в специальных таблицах, которые есть в конце любого учебника по статистике.

Таблица нормального распределения

Таблицы нормального распределения встречаются двух типов:

— таблица плотности;

— таблица функции (интеграла от плотности).

Таблица плотности используется редко. Тем не менее, посмотрим, как она выглядит. Допустим, нужно получить плотность для z = 1, т.е. плотность значения, отстоящего от матожидания на 1 сигму. Ниже показан кусок таблицы.

В зависимости от организации данных ищем нужное значение по названию столбца и строки. В нашем примере берем строку 1,0 и столбец 0, т.к. сотых долей нет. Искомое значение равно 0,2420 (0 перед 2420 опущен).

Функция Гаусса симметрична относительно оси ординат. Поэтому φ(z)= φ(-z), т.е. плотность для 1 тождественна плотности для -1, что отчетливо видно на рисунке.

Чтобы не тратить зря бумагу, таблицы печатают только для положительных значений.

На практике чаще используют значения функции стандартного нормального распределения, то есть вероятности для различных z.

В таких таблицах также содержатся только положительные значения. Поэтому для понимания и нахождения любых нужных вероятностей следует знать свойства стандартного нормального распределения.

Функция Ф(z) симметрична относительно своего значения 0,5 (а не оси ординат, как плотность). Отсюда справедливо равенство:

Это факт показан на картинке:

Значения функции Ф(-z) и Ф(z) делят график на 3 части. Причем верхняя и нижняя части равны (обозначены галочками). Для того, чтобы дополнить вероятность Ф(z) до 1, достаточно добавить недостающую величину Ф(-z). Получится равенство, указанное чуть выше.

Если нужно отыскать вероятность попадания в интервал (0; z), то есть вероятность отклонения от нуля в положительную сторону до некоторого количества стандартных отклонений, достаточно от значения функции стандартного нормального распределения отнять 0,5:

Для наглядности можно взглянуть на рисунок.

На кривой Гаусса, эта же ситуация выглядит как площадь от центра вправо до z.

Довольно часто аналитика интересует вероятность отклонения в обе стороны от нуля. А так как функция симметрична относительно центра, предыдущую формулу нужно умножить на 2:

Под кривой Гаусса это центральная часть, ограниченная выбранным значением –z слева и z справа.

Указанные свойства следует принять во внимание, т.к. табличные значения редко соответствуют интересующему интервалу.

Для облегчения задачи в учебниках обычно публикуют таблицы для функции вида:

Если нужна вероятность отклонения в обе стороны от нуля, то, как мы только что убедились, табличное значение для данной функции просто умножается на 2.

Теперь посмотрим на конкретные примеры. Ниже показана таблица стандартного нормального распределения. Найдем табличные значения для трех z: 1,64, 1,96 и 3.

Как понять смысл этих чисел? Начнем с z=1,64, для которого табличное значение составляет 0,4495. Проще всего пояснить смысл на рисунке.

То есть вероятность того, что стандартизованная нормально распределенная случайная величина попадет в интервал от 0 до 1,64, равна 0,4495. При решении задач обычно нужно рассчитать вероятность отклонения в обе стороны, поэтому умножим величину 0,4495 на 2 и получим примерно 0,9. Занимаемая площадь под кривой Гаусса показана ниже.

Таким образом, 90% всех нормально распределенных значений попадает в интервал ±1,64σ от средней арифметической. Я не случайно выбрал значение z=1,64, т.к. окрестность вокруг средней арифметической, занимающая 90% всей площади, иногда используется для проверки статистических гипотез и расчета доверительных интервалов. Если проверяемое значение не попадает в обозначенную область, то его наступление маловероятно (всего 10%).

Для проверки гипотез, однако, чаще используется интервал, накрывающий 95% всех значений. Половина вероятности от 0,95 – это 0,4750 (см. второе выделенное в таблице значение).

Для этой вероятности z=1,96. Т.е. в пределах почти ±2σ от средней находится 95% значений. Только 5% выпадают за эти пределы.

Еще одно интересное и часто используемое табличное значение соответствует z=3, оно равно по нашей таблице 0,4986. Умножим на 2 и получим 0,997. Значит, в рамках ±3σ от средней арифметической заключены почти все значения.

Так выглядит правило 3 сигм для нормального распределения на диаграмме.

С помощью статистических таблиц можно получить любую вероятность. Однако этот метод очень медленный, неудобный и сильно устарел. Сегодня все делается на компьютере. Далее переходим к практике расчетов в Excel.

Нормальное распределение в Excel

В Excel есть несколько функций для подсчета вероятностей или обратных значений нормального распределения.

Функция НОРМ.СТ.РАСП

Функция НОРМ.СТ.РАСП предназначена для расчета плотности ϕ( z ) или вероятности Φ(z) по нормированным данным (z).

z – значение стандартизованной переменной

интегральная – если 0, то рассчитывается плотность ϕ( z ) , если 1 – значение функции Ф(z), т.е. вероятность P(Z

Источник