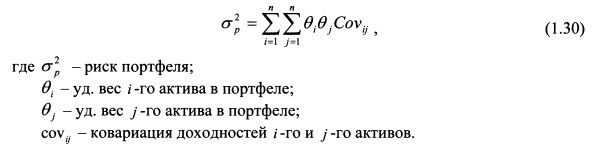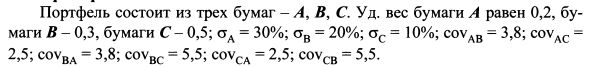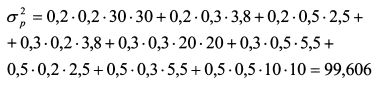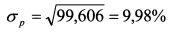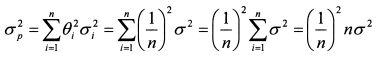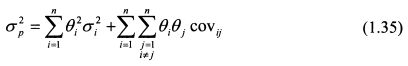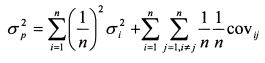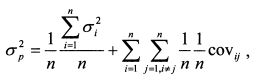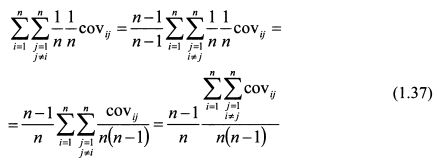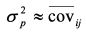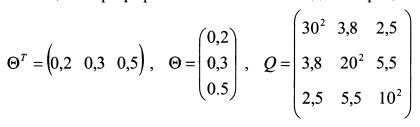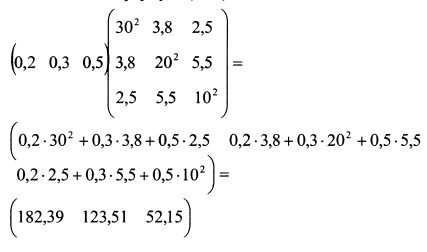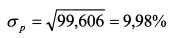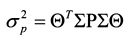Дисперсия (вариация) | Variance
В статистике дисперсия или вариация (англ. Variance) является показателем, который используется для оценки разброса значений случайной величины относительно ее математического ожидания. В портфельной теории дисперсия доходности является мерой риска, связанного с инвестированием в определенный актив или портфель активов.
Формула
Если известен полный набор вероятностей исхода события, что крайне редко встречается на практике, для расчета величины дисперсии используется следующая формула:
где ki – доходность ценной бумаги или актива при i-ом варианте исхода событий;
— ожидаемая доходность ценной бумаги или актива;
pi – вероятность i-го варианта исхода событий.
В реальной практике инвестирования аналитику обычно доступны исторические данные о доходности ценной бумаги или актива. Если он располагает всем массивом информации, то есть оценивает дисперсию на основании генеральной совокупности данных, необходимо использовать следующую формулу:
где ki – i-ое значение доходности ценной бумаги;
— средняя доходность ценной бумаги;
n – количество наблюдений.
Однако чаще оценку риска проводят на основании некоторой выборки из генеральной совокупности данных, поэтому для получения несмещенной оценки дисперсии количество степеней свободы уменьшают на 1. В этом случае формула для ее оценки будет выглядеть следующим образом:
Интерпретации дисперсии
Чем выше значение дисперсии, то есть чем выше разброс доходности актива или портфеля активов относительно его ожидаемой доходности, тем выше будет уровень риска. Напротив, низкие значения этого показателя свидетельствуют о низком уровне риска, связанного с осуществлением инвестиций.
Также следует отметить, что квадратный корень от дисперсии случайной величины является ее среднеквадратическим отклонением.
Пример расчета
Пример 1. Предположим, что финансовому аналитику необходимо произвести оценку риска, связанного с приобретением акций Компании А и Компании Б. Предположим, что аналитику известен полный набор вероятностей событий, который представлен в таблице.
Ожидаемая доходность для акций Компании составит 18,75%, а для акций Компании Б 19,45%.
А = 7*0,05+15*0,2+18*0,5+24*0,2+32*0,05 = 18,75%
Б = -24*0,05+8*0,2+20*0,5+31*0,2+57*0,05 = 19,45%
В свою очередь, дисперсия доходности акций Компании А будет равна 24,288%, а акций Компании Б 217,948%.
σ 2 А = (7-18,75)2*0,05 + (15-18,75)2*0,2 + (18-18,75)2*0,5 + (24-18,75)2*0,2 + (32-18,75)2*0,05 = 24,288%
σ 2 Б = (-24-19,45)2*0,05 + (8-19,45)2*0,2 + (20-19,45)2*0,5 + (31-19,45)2*0,2 + (57-19,45)2*0,05 = 217,948%
Хотя ожидаемая доходность у акций обеих компаний практически одинаковая, риски инвестирования в акции Компании Б будут существенно выше.
Пример 2. Историческая доходность акций за последние пять лет представлена в таблице.
Средняя доходность акции составит 5,784%.
= (5,78+12,33-7,21+8,25+9,77)/5 = 5,784%
Поскольку анализируется не вся генеральная совокупность данных, а только выборку из нее, оценка дисперсии составит 58,42%.
σ 2 = ((5,78-5,784)2 + (12,33-5,784)2 + (-7,21-5,784)2 + (8,25-5,784)2 + (9,77-5,784)2)/(5-1) = 58,42%
Источник
Определение отклонения портфеля
Дисперсия портфеля – это измерение риска того, как фактические доходы из набора ценные бумаги составление портфеля колеблется со временем. Это портфолио дисперсия статистика рассчитывается с использованием Стандартное отклонение каждой ценной бумаги в портфеле, а также корреляции каждой пары безопасности в портфеле.
Дисперсия портфеля эквивалентна квадрату стандартного отклонения портфеля.
Дисперсия портфеля смотрит на ковариационная или коэффициенты корреляции для ценных бумаг в портфеле. Как правило, более низкая корреляция между ценными бумагами в портфеле приводит к меньшей дисперсии портфеля.
Дисперсия портфеля рассчитывается путем умножения квадрата веса каждой ценной бумаги на соответствующую дисперсию и сложения в два раза средневзвешенное умноженный вес по ковариации всех индивидуальных пар безопасности.
- Дисперсия портфеля является мерой общего риска портфеля и является квадратом стандартного отклонения портфеля.
- Дисперсия портфеля учитывает вес и дисперсию каждого актива в портфеле, а также их ковариации.
- Дисперсия портфеля (и стандартное отклонение) определяют ось риска эффективной границы в современной теории портфеля.
Наиболее важным качеством отклонения портфеля является то, что его стоимость представляет собой взвешенную комбинацию отдельных отклонений каждого из активов, скорректированных по их ковариациям. Это означает, что общая дисперсия портфеля ниже простого средневзвешенного значения отдельных дисперсий акций в портфеле.
Уравнение для дисперсии портфеля портфеля с двумя активами, простейшего расчета дисперсии портфеля, учитывает пять переменных:
- w1 = вес портфеля первого актива
- w2 = вес портфеля второго актива
- σ1 = стандартное отклонение первого актива
- σ2 = стандартное отклонение второго актива
- cov (1,2) = ковариация двух активов, которая может быть выражена как: p (1,2) σ1σ2, где p (1,2) – коэффициент корреляции между двумя активами
Формула для дисперсии в портфеле из двух активов:
По мере роста количества активов в портфеле условия в формуле для дисперсии растут в геометрической прогрессии. Например, портфель из трех активов имеет шесть условий в расчете дисперсии, а портфель из пяти активов – 15.
Например, предположим, что есть портфель, состоящий из двух акций. Акция стоит 50 000 долларов США и имеет стандартное отклонение 20%. Акция B стоит 100 000 долларов США и имеет стандартное отклонение 10%. Корреляция между двумя акциями составляет 0,85. Учитывая это, вес портфеля Акции 33,3% и 66,7% для Акции В. С учетом этой информации в формулу, дисперсия рассчитывается следующим образом:
Дисперсия = (33,3% ^ 2 х 20% ^ 2) + (66,7% ^ 2 х 10% ^ 2) + (2 х 33,3% х 20% х 66,7% х 10% х 0,85) = 1,64%
Дисперсия не очень легкая статистика для самостоятельной интерпретации, поэтому большинство аналитиков вычисляют стандартное отклонение, которое является просто квадратным корнем дисперсии. В этом примере квадратный корень из 1,64% составляет 12,82%.
Современная теория портфеля – это основа для построения инвестиционного портфеля. В качестве основной предпосылки MPT ��спользует идею о том, что рациональные инвесторы хотят максимизировать доходность, а также минимизировать риск, иногда измеряемый с помощью волатильности. Инвесторы ищут то, что называется эффективной границей, или самым низким уровнем или риском и волатильностью, при которой может быть достигнут целевой доход.
Риск в портфелях МРТ снижается за счет инвестирования в некоррелированные активы. Активы, которые могут быть рискованными сами по себе, могут фактически снизить общий риск портфеля, вводя инвестиции, которые будут расти, когда другие инвестиции падают. Эта уменьшенная корреляция может уменьшить дисперсию теоретического портфеля. В этом смысле доходность отдельной инвестиции менее важна, чем ее общий вклад в портфель с точки зрения риска, доходности и диверсификации.
Уровень риска в портфеле часто измеряется с использованием стандартного отклонения, которое рассчитывается как квадратный корень из дисперсии. Если точки данных находятся далеко от среднего значения, дисперсия высока, и общий уровень риска в портфеле также высок. Стандартное отклонение является ключевым показателем риска используется портфельными менеджерами, финансовыми консультантами и институциональными инвесторами. Управляющие активами обычно включают стандартное отклонение в свои отчеты об эффективности.
Источник
1.2.6. Риск портфеля, состоящего из нескольких активов
Выше мы рассмотрели портфель, состоящий из двух бумаг, и сделали общие выводы относительно его формирования. Данные выводы верны и для портфеля, объединяющего большее количество активов.
Рассмотрим, как определяется риск портфеля, состоящего из нескольких бумаг. Он рассчитывается по формуле:
В формуле (1.30) стоит знак двойной суммы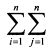 
. Это означает, что, раскрывая его, мы должны вначале взять значение i = 1 и умножить на него все значения j от 1 до п. Затем повторить данную операцию, но уже для i = 2, и т.д.
В итоге получим п слагаемых. Чтобы проиллюстрировать использование данной формулы, рассчитаем риск портфеля, состоящего из трех бумаг. Если портфель будет состоять из большего количества активов, техника расчета останется такой же.
Определить риск портфеля.
Дисперсия портфеля равна:
Стандартное отклонение портфеля составляет:
Как было отмечено выше, для портфеля, состоящего из двух активов с корреляцией доходностей +1, риск представляет собой средневзвешенный риск входящих в него активов. Поэтому для такого случая не наблюдается уменьшение риска, т.е. уменьшение его дисперсии, а происходит только его усреднение. Данный принцип сохраняется и для портфеля, насчитывающего много бумаг с корреляцией доходности +1.
Если портфель состоит из активов с корреляцией равной нулю, его риск рассчитывается по формулам:
Когда бумаги имеют одинаковую дисперсию и уд. вес, формулу (1.31) можно преобразовать следующим образом:
Соответственно формула (1.32) принимает вид:
Как следует из формул (1.33) и (1.34), риск портфеля убывает по мере увеличения количества входящих в него активов.
Формулу (1.30) можно переписать в следующей форме:
Если в портфель включить бумаги в равном удельном весе, формула (1.35) запишется как:
Умножим и разделим второе слагаемое формулы (1.36) на (n-1) и преобразуем его:
В выражении (1.37) величина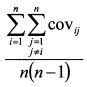 
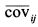
представляет собой среднюю ковариацию доходностей активов, входящих в портфель, так как в ее числителе стоит сумма ковариации, а в знаменателе — их число. Обозначим среднюю ковариацию через 
. Тогда формулу (1.35) можно записать как:
При увеличении количества активов в портфеле значение первого слагаемого в формуле (1.38) будет уменьшаться и при большом значении n оно приблизится к нулю. У второго слагаемого выражение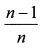 
будет стремиться к единице. Поэтому формула (1.38) принимает вид:
Таким образом, при включении в портфель большого количества бумаг и при условии, что их уд. веса приблизительно одинаковы, риск портфеля по своей величине близок к значению средней ковариации доходностей входящих в него активов.
В настоящей главе мы рассчитывали риск портфеля на основе формулы (1.30). Однако следует отметить, что в современной литературе вместо данной формулы часто используется ее аналог, записанный в матричной форме. Поэтому рассмотрим вопрос расчета риска портфеля с помощью матриц. Необходимые сведения из матричного исчисления приведены в приложении 4 к настоящей главе.
Риск портфеля ценных бумаг, представленный дисперсией его доходности, с помощью матриц можно записать как:
В качестве иллюстрации использования формулы (1.39) возьмем условия примера 1 настоящего параграфа. Запишем состав каждой матрицы:
Важно: актуальное предложение по поводу компенсации до 100% комиссии, взимаемой Вашим брокером.
В матрице Q по диагонали расположены дисперсии доходностей активов, а оставшиеся элементы представляют собой ковариации доходностей бумаг между собой. Риск портфеля равен:
Осуществим вычисления в формуле (1.40) последовательно:
Стандартное отклонение составляет:
Матрица ковариаций Q равна SPS, где Р — корреляционная матрица размера пхп ; ? — матрица стандартных отклонений размера пхп; п — количество активов в портфеле. Поэтому формулу (1.39) можно представить еще следующим образом:
Данная формула для двух активов раскрывается следующим образом:
Источник