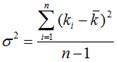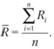Дисперсия доходности инвестиций это

2 Дисперсия и стандартное отклонение.

Дисперсия — это мера разброса возможных исходов относительно ожидаемого значения. Следовательно, чем выше дисперсия, тем больше разброс, а значит и риск. Формула для расчета дисперсии следующая:

(2.4)

где ri — доходность актива;
r сред — ожидаемая (средняя) доходность актива;
n — число наблюдений.
Показатель дисперсии измеряют в процентах в квадрате и так как такая интерпретация очень непривычна и тяжела, в качестве другого показателя отклонения значений доходности от ожидаемого значения используется «среднее квадратическое отклонение» (стандартное отклонение), которое является квадратным корнем из дисперсии.

(2.5)

Приведем пример расчета дисперсии и стандартного отклонения при помощи Excel на основе имеющихся данных РАО ЕЭС, Лукойла и Ростелекома, пользуясь встроенными функциями ДИСП и СТАНДОТКЛОН.

Рисунок 2.16 – Вид с формулами
В результате получим:

Рисунок 2.17 – Дисперсии и стандартные отклонения
Итак, можно смело констатировать, что наиболее рискованной бумагой является Ростелеком. Ожидаемая ежемесячная доходность -1.08% при риске 9.44%.а наименее рискованной бумагой является Лукойл. Необходимо отметить, что не всегда актив, имеющий наибольшее стандартного отклонение является самым рискованным. Поэтому, прежде чем использовать стандартное отклонение в качестве меры относительного риска нужно рассчитать риск, приходящийся на единицу доходности при помощи коэффициента вариации. Этот показатель рассмотрен не будет, т.к. применительно к портфельной теории он не обязателен.
Зная ожидаемые доходности и показатели риска (стандартное отклонение), необходимо произвести еще ряд расчетов по определению коэффициентов ковариации и корреляция. После расчета данных коэффициентов станет возможным формирование портфелей, соответствующих нашим требованиям по риску и доходности.

Источник

Дисперсия (вариация) | Variance

В статистике дисперсия или вариация (англ. Variance) является показателем, который используется для оценки разброса значений случайной величины относительно ее математического ожидания. В портфельной теории дисперсия доходности является мерой риска, связанного с инвестированием в определенный актив или портфель активов.

Формула

Если известен полный набор вероятностей исхода события, что крайне редко встречается на практике, для расчета величины дисперсии используется следующая формула:

где k_i – доходность ценной бумаги или актива при i-ом варианте исхода событий;

— ожидаемая доходность ценной бумаги или актива;

p_i – вероятность i-го варианта исхода событий.

В реальной практике инвестирования аналитику обычно доступны исторические данные о доходности ценной бумаги или актива. Если он располагает всем массивом информации, то есть оценивает дисперсию на основании генеральной совокупности данных, необходимо использовать следующую формулу:

где k_i – i-ое значение доходности ценной бумаги;

— средняя доходность ценной бумаги;

n – количество наблюдений.

Однако чаще оценку риска проводят на основании некоторой выборки из генеральной совокупности данных, поэтому для получения несмещенной оценки дисперсии количество степеней свободы уменьшают на 1. В этом случае формула для ее оценки будет выглядеть следующим образом:

Интерпретации дисперсии

Чем выше значение дисперсии, то есть чем выше разброс доходности актива или портфеля активов относительно его ожидаемой доходности, тем выше будет уровень риска. Напротив, низкие значения этого показателя свидетельствуют о низком уровне риска, связанного с осуществлением инвестиций.

Также следует отметить, что квадратный корень от дисперсии случайной величины является ее среднеквадратическим отклонением.

Пример расчета

Пример 1. Предположим, что финансовому аналитику необходимо произвести оценку риска, связанного с приобретением акций Компании А и Компании Б. Предположим, что аналитику известен полный набор вероятностей событий, который представлен в таблице.

Ожидаемая доходность для акций Компании составит 18,75%, а для акций Компании Б 19,45%.

_А = 7*0,05+15*0,2+18*0,5+24*0,2+32*0,05 = 18,75%

_Б = -24*0,05+8*0,2+20*0,5+31*0,2+57*0,05 = 19,45%

В свою очередь, дисперсия доходности акций Компании А будет равна 24,288%, а акций Компании Б 217,948%.

σ 2 _А = (7-18,75)2*0,05 + (15-18,75)2*0,2 + (18-18,75)2*0,5 + (24-18,75)2*0,2 + (32-18,75)2*0,05 = 24,288%

σ 2 _Б = (-24-19,45)2*0,05 + (8-19,45)2*0,2 + (20-19,45)2*0,5 + (31-19,45)2*0,2 + (57-19,45)2*0,05 = 217,948%

Хотя ожидаемая доходность у акций обеих компаний практически одинаковая, риски инвестирования в акции Компании Б будут существенно выше.

Пример 2. Историческая доходность акций за последние пять лет представлена в таблице.

Средняя доходность акции составит 5,784%.

= (5,78+12,33-7,21+8,25+9,77)/5 = 5,784%

Поскольку анализируется не вся генеральная совокупность данных, а только выборку из нее, оценка дисперсии составит 58,42%.

σ 2 = ((5,78-5,784)2 + (12,33-5,784)2 + (-7,21-5,784)2 + (8,25-5,784)2 + (9,77-5,784)2)/(5-1) = 58,42%

Источник

5 ключевых метрик инвестиционного портфеля

Чем большую доходность хочет инвестор, тем более рисковые инструменты ему придется использовать. Задача инвестора — найти такое сочетание активов, при котором соотношение доходности и риска станет наилучшим.

Рассмотрим 5 ключевых метрик, которые помогут в этом. Эти параметры выдает большинство сервисов для анализа ценных бумаг и портфелей, в частности сайт Portfolio Visualizer, о работе с которым у нас есть статья.

📈 Среднегодовая доходность (CAGR)

Показывает среднегодовой темп роста портфеля на основе стартового и конечного капитала, а также срока инвестирования. Это среднегеометрическая доходность, учитывающая сложный процент, в отличие от средней арифметической доходности.

CAGR подходит, если инвестор не пополняет портфель и не выводит из него деньги в течение срока инвестирования. Если есть движение средств, то лучше использовать IRR — внутреннюю норму доходности

⏩ Стандартное отклонение (st. dev., σ)

Показывает, насколько волатильна доходность портфеля, то есть насколько он рискован. Считается как квадратный корень из дисперсии — разброса значений доходности от ее среднего значения.

Чем выше стандартное отклонение доходности актива или портфеля, тем выше риск. Чтобы снизить риск, в портфеле стоит сочетать инструменты с низким коэффициентом корреляции — о нем далее

🌀 Корреляция (correlation)

Показывает, насколько похоже ведут себя инструменты. Коэффициент корреляции может быть в диапазоне от −1 до 1.

Корреляция, близкая к единице, говорит о тесной взаимосвязи двух активов. Значение, близкое к нулю, показывает, что явной связи нет, а при значении около −1 активы движутся разнонаправленно.

Чем ниже коэффициент корреляции, тем лучше активы дополняют друг друга в портфеле. В теории, взяв два актива с корреляцией −1, можно достичь нулевого риска портфеля

🅱️ Бета (beta, β)

Показывает, как отдельный актив или портфель ведут себя относительно рынка. В случае с американскими акциями бета рассчитывается относительно индекса S&P 500, в случае с российскими акциями — относительно индекса Мосбиржи.

Бета 1 значит, что актив идентичен рынку. Если более 1, то актив коррелирует с рынком, но ведет себя более волатильно: сильнее растет или сильнее падает. Если бета от 0 до 1, то актив движется однонаправленно с рынком, а риск меньше рыночного.

При бете от 0 до −1 актив и рынок движутся в разные стороны, а актив стабильнее. При бете меньше −1 актив и рынок тоже движутся разнонаправленно, но актив волатильнее

💼 Коэффициент Шарпа (Sharpe ratio)

Показывает эффективность портфеля с точки зрения доходности и риска.

Считается так: (Доходность портфеля − Безрисковая процентная ставка) / Стандартное отклонение. Безрисковая ставка — это, например, доходность вкладов или векселей казначейства США.

Чем выше коэффициент Шарпа, тем большую прибыль извлекает инвестор на единицу риска и тем эффективнее стратегия

Источник

Дисперсия как мера финансового инвестиционного риска. Оценка дисперсии и среднеквадратического отклонения доходности ценных бумаг.

В статистике дисперсия или вариация является показателем, который используется для оценки разброса значений случайной величины относительно ее математического ожидания. В портфельной теории дисперсия доходности является мерой риска, связанного с инвестированием в определенный актив или портфель активов.

где k_i – доходность ценной бумаги или актива при i-ом варианте исхода событий;

— ожидаемая доходность ценной бумаги или актива;

p_i – вероятность i-го варианта исхода событий.

где k_i – i-ое значение доходности ценной бумаги;

— средняя доходность ценной бумаги;

n – количество наблюдений.

Также следует отметить, что квадратный корень от дисперсии случайной величины является ее среднеквадратическим отклонением.

Под риском можно понимать вероятность возникновения каких-либо отклонений от ожидаемого события. Основополагающими мерами риска финансового актива являются такие показатели, как стандартное отклонение (σ) и дисперсия (D = σ2) сто доходности. В качестве синонима понятия «стандартное отклонение» используют также термин «волатильность». Стандартное отклонение и дисперсия доходности актива отражают степень возможного разброса его фактической доходности вокруг его средней (наиболее вероятной) доходности. Данные меры риска можно определить на основе прошлых данных статистики доходности актива.

Доходность актива на рассматриваемом интервале определяется следующим образом:

где St-1 – стоимость актива в начале интервала наблюдения; St – стоимость актива в конце интервала наблюдения.

Пусть имеются значения доходности акции за п равных интервалов наблюдения. За первый интервал она составила величину R1, за второй – R2 и т.д., за п-й интервал – Rn

Средняя доходность актива за наблюдаемый период (R) рассчитывается по формуле

Дисперсия доходности актива определяется как мера разброса наблюдаемой доходности (в процентах) от ее математического ожидания (средней величины). Формула генеральной дисперсии имеет вид

В случае если количество наблюдений незначительно (меньше 30), то для получения несмещенной оценки рекомендуется использовать так называемую исправленную дисперсию:

Показателем, характеризующим относительный уровень риска финансового актива, является стандартное отклонение его доходности от ожидаемой (средней за период):

При этом оценка допустимого уровня стандартного отклонения является субъективной и характеризует готовность инвестора принимать риск с учетом возможной доходности финансового актива.

Источник