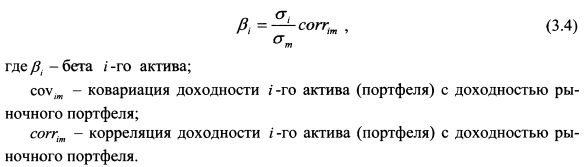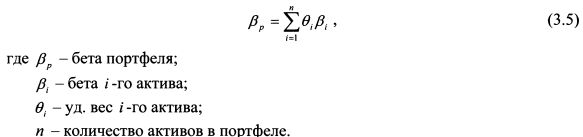D. Указанных данных недостаточно для решения задачи



Пусть Х и Y — случайные величины, М — математическое ожидание, М(Х)=3; М(Y)=5. Найти М(8Х — 3Y).
C. 9
Даны 3 актива. Известно, что ожидаемая доходность первого актива X = 30%, ожидаемая доходность второго актива Y = 20%. Определить ожидаемую доходность актива Z, если известно, что Z=9X-6Y+80.
A. 230
Даны 3 актива. Известно, что ожидаемая доходность первого актива X = 25%, ожидаемая доходность второго актива Y = 40%. Определить ожидаемую доходность актива Z, если известно, что Z=23X-15Y+75.
A. 50
Даны 3 актива. Известно, что ожидаемая доходность первого актива X = 50%, ожидаемая доходность второго актива Y = 65%. Определить ожидаемую доходность актива Z, если известно, что Z=17X+12Y-80.
A. 1550
Портфель инвестора составлен из акций А и B. Ожидаемая доходность акции А равна 10%, ожидаемая доходность акции B равна 15%. Какова ожидаемая доходность портфеля, если удельные веса акций А и В в портфеле составляют соответственно 60% и 40%?
B. 12%
Портфель инвестора составлен из акций А и B. Ожидаемая доходность акции А равна 20%, ожидаемая доходность акции B равна 30%. Какова ожидаемая доходность портфеля, если удельные веса акций А и В в портфеле составляют соответственно 50% и 50%?
B. 25%
Портфель инвестора составлен из акций А и B. Ожидаемая доходность акции А равна 30%, ожидаемая доходность акции B равна 40%. Какова ожидаемая доходность портфеля, если удельные веса акций А и В в портфеле составляют соответственно 30% и 70%?
B. 37%
Прогноз инвестора относительно возможных сценариев доходности акций компаний А и В с учетом их вероятностей (Р) в следующем периоде представлен в таблице:
Определить ожидаемую доходность портфеля, если уд. веса акций А и В в портфеле составляют соответственно 30% и 70%.
A. 17,30%
Прогноз инвестора относительно возможных сценариев доходности акций компаний А и В с учетом их вероятностей (Р) в следующем периоде представлен в таблице:
Определить ожидаемую доходность портфеля, если уд. веса акций А и В в портфеле составляют соответственно 40% и 60%.
A. 19,60%
Прогноз инвестора относительно возможных сценариев доходности акций компаний А и В с учетом их вероятностей (Р) в следующем периоде представлен в таблице:
Определить ожидаемую доходность портфеля, если уд. веса акций А и В в портфеле составляют соответственно 70% и 30%.
A. 31,85%
Прогноз инвестора относительно возможных сценариев доходности акций компаний А и В с учетом их вероятностей (Р) в следующем периоде представлен в таблице:
Определить ожидаемую доходность портфеля, если уд. веса акций А и В в портфеле составляют соответственно 50% и 50%.
A. 30,50%
Пусть Х — случайная величина, М — математическое ожидание, D — дисперсия случайной величины, М(Х)=0,5, D(X)=2,25. Найти D(Х + 2).
B. 2,25
Пусть Х — случайная величина, М — математическое ожидание, D — дисперсия случайной величины, М(Х)=0,5, D(X)=1,5. Найти D(2Х + 1).
C. 6
Пусть Х и Y — случайные величины, D — дисперсия случайной величины, D(Х)=0,5, D(Y)=1,5. Найти D(Х + Y).
D. Указанных данных недостаточно для решения задачи
Пусть Х и Y — независимые случайные величины, D — дисперсия случайной величины, D(Х)=0,5, D(Y)=1,5. Найти D(Х + Y).
B. 2
Пусть Х и Y — случайные величины, D — дисперсия случайной величины, К — ковариация, D(Х)=0,5, D(Y)=1,5, К(Х,Y)= -0,5. Найти D(Х + Y).
C. 1
Случайные величины Х и Y независимы. Дисперсии величин D(Х)=3 и D(Y)=8. Найти дисперсию случайной величины Z=7Х-4Y+11.
B. 275

Случайные величины Х и Y независимы. Дисперсии величин D(Х)=5 и D(Y)=9. Найти дисперсию случайной величины Z=2Х-Y+5.
B. 29
Случайные величины Х и Y независимы. Дисперсии величин D(Х)=7 и D(Y)=9. Найти дисперсию случайной величины Z=12Х-8Y+30.
B. 1584
Найти дисперсию случайной величины Z=6Х-3Y+5, если известно, что случайные величины X и Y независимы и D(X)=2,5, D(Y)=2.
A. 108
Доходность актива за 3 года представлена в таблице:
Определить риск актива, представленный показателями выборочной дисперсии и стандартного отклонения доходности.
A. 10,67; 3,27%
Доходность актива за 3 года представлена в таблице:
Определить риск актива, представленный показателями выборочной дисперсии и стандартного отклонения доходности.
A. 72,67; 8,52%
Доходность актива за 3 года представлена в таблице:
Определить риск актива, представленный показателями выборочной дисперсии и стандартного отклонения доходности.
A. 162,67; 12,75%
Доходность актива за 3 года представлена в таблице:
Определить риск актива, представленный показателями выборочной дисперсии и стандартного отклонения доходности.
A. 12,67; 3,56%
Пусть Х — случайная величина, М — математическое ожидание, D — дисперсия случайной величины, М(Х)=2, D(X)=0,25. Укажите верное утверждение из следующих:
I. Х принимает значения только в интервале от 1,75 до 2,25;
II. Х принимает значения только в интервале от 0,5 до 3,5;
III. Х принимает только положительные значения.
Источник
3.1.3. Бета
Для измерения рыночного риска актива используется величина бета. Она показывает зависимость между доходностью актива и доходностью рынка. Доходность рынка — это доходность рыночного портфеля. Поскольку невозможно сформировать портфель, в который бы входили все финансовые активы, то в качестве него принимается какой-либо индекс с широкой базой. Поэтому доходность рынка — это доходность портфеля, представленного выбранным индексом. Величина бета представляет собой не что иное как угловой коэффициент наклона линии регрессии доходности актива на доходность индекса. В связи с этим она рассчитывается по формуле:
Поскольку величина бета определяется по отношению к рыночному портфелю, то бета самого рыночного портфеля равна единице, так как ковариация доходности рыночного портфеля с самим собой есть его дисперсия, отсюда:
Бета актива без риска равна нулю, потому что нулю равна ковариация доходности актива без риска с доходностью рыночного портфеля.
Величина /5[^актива говорит о том, насколько его риск больше или меньше риска рыночного портфеля. Активы с бетой больше единицы обладают большим риском, чем рыночный портфель, а активы с бетой меньше единицы — менее рискованны чем рыночный портфель. Относительно величины бета активы делят на агрессивные и защитные. Бета агрессивных активов больше единицы, защитных — меньше единицы. Если бета актива равна единице, то его риск равен риску рыночного портфеля.
Бета может быть как положительной, так и отрицательной величиной. Положительное значение беты говорит о том, что доходности актива и рынка при изменении конъюнктуры изменяются в одном направлении. Отрицательная бета показывает, что доходности актива и рынка меняются в противоположных направлениях.
Бета актива показывает, в какой степени доходность актива (и соответственно его цена) будет реагировать на действие рыночных сил. Зная бету актива, можно оценить, насколько должна измениться его ожидаемая доходность при изменении ожидаемой доходности рынка. Например, бета бумаги равна +2. Это значит, что при увеличении ожидаемой доходности рыночного портфеля на 1% следует в среднем ожидать роста доходности бумаги на 2%, и наоборот, при уменьшении доходности рыночного портфеля на 1% следует в среднем ожидать снижения доходности бумаги на 2%. Поскольку бета бумаги больше единицы, то она рискованнее рыночного портфеля. Если бета бумаги равна 0,5, то при увеличении ожидаемой доходности рынка на 1% ожидаемая доходность бумаги в среднем должна возрасти только на 0,5%. Напротив, при снижении доходности рынка на 1% доходность бумаги уменьшится в среднем только на 0,5%. Таким образом, риск данной бумаги меньше риска рынка. Если бета равна -2, то при повышении доходности рыночного портфеля на 1% доходность актива снизится на 2% и наоборот, активы с отрицательной бетой являются ценными инструментами для диверсификации портфеля, поскольку в этом случае можно построить портфель с «нулевой бетой», который не будет нести риска. Здесь, однако, следует помнить, что такой портфель не аналогичен активу без риска, так как при нулевом значении беты он не будет содержать только рыночного риска. В то же время данный портфель сохранит риск нерыночный.
Важно: актуальное предложение по поводу компенсации до 100% комиссии, взимаемой Вашим брокером.


Зная величину беты для каждого из активов, вкладчик может легко сформировать портфель требуемого уровня риска и доходности. Бета портфеля — это средневзвешенное значение величин бета активов, входящих в портфель, где весами выступают их удельные веса в портфеле. Она рассчитывается по формуле:
Формулу (3.5) можно получить за счет следующих преобразований. По определению бета портфеля равна отношению ковариации доходностей портфеля и рынка (covpm) к дисперсии доходности рынка:
Ковариация доходности портфеля с рынком представляет собой сумму ковариации каждой бумаги портфеля с учетом ее уд. веса в портфеле с рынком. Поэтому формулу (3.6) можно записать как:
Источник
Вопросы и ответы к базовому экзамену (с 16 сентября 2012). Определить коэффициент корреляции доходностей акций
www.forexam.ru
Определить коэффициент корреляции доходностей акций.
A. Для ответа недостаточно данных
C. Минус один
Код вопроса: 4.2.136
Доходности акций А и В могут принимать только два значения, как
показано в таблице:
Доходность А Доходность В
Определить ожидаемую доходность портфеля, если уд. веса акций А и В
в портфеле составляют соответственно 40% и 60%.
A. 19,6%
Код вопроса: 4.2.143
Прогноз инвестора относительно возможных сценариев доходности акций
компаний А и В с учетом их вероятностей p в следующем периоде
представлен в таблице:
2-й сценарий 8% 10%
Определить коэффициент корреляции доходностей акций.
A. Для ответа недостаточно данных.
D. 0
Код вопроса: 4.2.137
Даны следующие вероятности роста доходности акций компаний «А», «В»
и «С»: P(A)=0,8; P(B)=0,7; P(C)=0,9. Какова вероятность того, что
доходности акций трех компаний вырастут?
A. 0,504
Код вопроса: 4.2.138
Даны следующие вероятности роста доходности акций компаний «А», «В»
и «С»: P(A)=0,8; P(B)=0,7; P(C)=0,9. Какова вероятность того, что
вырастет доходность только акций компании «В»?
C. 0,014
Код вопроса: 4.2.139
Даны следующие вероятности роста доходности акций компаний «А», «В»
и «С»: P(A)=0,8; P(B)=0,7; P(C)=0,9. Какова вероятность того, что
вырастет доходность акций хотя бы одной компании?
A. 0,994
Код вопроса: 4.2.140
Даны 3 актива. Известно, что ожидаемая доходность первого актива X =
30%, ожидаемая доходность второго актива Y = 20%. Определить
ожидаемую доходность актива Z, если известно, что Z=9X-6Y+80.
A. 230
Код вопроса: 4.2.141
Найти дисперсию случайной величины Z=6Х-3Y+5, если известно, что
случайные величины X и Y независимы и D(X)=2,5, D(Y)=2.
A. 108
Код вопроса: 4.2.142
Прогноз инвестора относительно возможных сценариев доходности акций
компаний А и В с учетом их вероятностей p в следующем периоде
представлен в таблице:
Определить ожидаемую доходность портфеля, если уд. веса акций А и В
в портфеле составляют соответственно 70% и 30%.
A. 31,85%
Код вопроса: 4.2.144
Прогноз инвестора относительно возможных сценариев доходности акций
компаний А и В с учетом их вероятностей p в следующем периоде
представлен в таблице:
Определить ожидаемую доходность портфеля, если уд. веса акций А и В
в портфеле составляют соответственно 50% и 50%.
A. 30,5%
обсуждение вопросов, решение задач, онлайн-тренажер ФСФР
41 / 124 










































































|
|
|
|
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник