Что является шагом при решении задач по распределению инвестиций

Постановка и решение задачи оптимального распределения инвестиций

Экономическая эффективность капитальных вложений (инвестиций) — одна из важнейших проблем планирования, характеризующая целесообразность вложений финансовых и других средств.

Рационального распределения инвестиций можно достигнуть лишь на основе тщательных экономических расчетов, дающих возможность определить пути достижения максимальной отдачи, т.е.

При установлении структуры инвестиций на государственном уровне необходимо исходить из предусмотренных темпов развития отраслей экономики страны, обеспеченности их основными фондами и степени использования мощностей, объема сырья и материалов, поступающих из смежных отраслей, и ряда других факторов.

Межотраслевое распределение инвестиций должно сопровождаться распределением вложений внутри отрасли и, в частности, между предприятиями, выпускающими однородную продукцию. Критерием для оптимального распределения инвестиций могут служить максимальная прибыль, максимальный суммарный прирост продукции, максимальное снижение себестоимости, максимальная занятость населения и т.п.

Задача оптимального распределения инвестиций по своей природе комбинаторная. Например, при определении фондоотдачи от 10 млрд руб. в четыре отрасли промышленности необходимо перебрать все распределения числа 10 на четыре группы. При условии распределения только из целых чисел необходимо подсчитать 286 комбинаций:

(10, 0, 0, 0); (9, 1, 0, 0); (9, 0, 1, 0); (9, 0, 0, 1) . ;

(8, 1, 1, 0); (8, 1, 0, 1); (8, 0, 1, 1); (8, 2, 0, 0); (8, 0, 2, 0); (8, 0, 0, 2);

(4, 3, 2, 1); . (4, 2, 2, 2); .

Если требуется дополнительно определить оптимальное решение задачи в случае, когда инвестиции в целом составляют 9, 8, 7, . 1 млрд руб., то необходимо провести большой объем вычислительной работы.

Метод динамического программирования позволяет находить оптимальное решение задач по распределению однородных средств между объектами при значительно меньшем, по сравнению с комбинаторным способом решения, объеме вычислительной работы.

В общем виде математическая постановка задач по распределению однородных средств (капитальных вложений, машин, сырья и т.д.) между объектами формулируется следующим образом: найти значения неизвестных xv х2, . х, . хп, т.е. план распределения, удовлетворяющий условиям:

обращающие в максимум функцию

(4.2)

где— сумма возможных вложений по j-му объекту (отрасль, предприятие, цех, участок);

— фондоотдача по предполагаемому j-му объекту, т.е. функция отдачи капитальных вложений (прибыль, прирост продукции и т.д.).

Алгоритм, предложенный Беллманом, справедлив для функцийлюбого вида и является одним из простейших примеров применения динамического программирования. Идея алгоритма состоит в том, что последовательно решаются задачи оптимального распределения средств между первыми j объектами (здесь j принимает значения 1, 2, 3, . n). Последняя из этих задач является решением поставленной.

В задаче по распределению средств между объектами всегда предполагаются известными значения функций f.(x) при всех возможных значениях аргументов (табл. 4.7).

Источник

Динамическое программирование. Задача о распределении инвестиций — видеоурок с решением задачи в Excel

>Ниже приведено условие задачи и текстовая часть решения. Закачка полного решения, файлы doc и xls в архиве zip, начнется автоматически через 10 секунд. Видеоурок по решению этих задач — внизу страницы.

Указать оптимальные размеры и потоки инвестирования, если прибыль от вложений (Х i ) в проекты (А i ) распределилась следующим образом:

Теперь для решения этой задачи воспользуемся Excel .

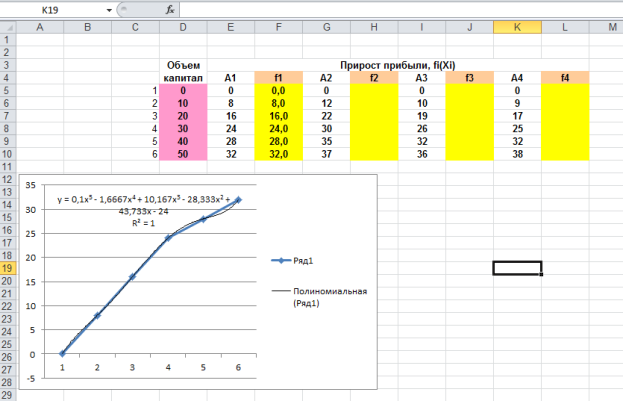
Для этого выделим шаги тренда t i , вложения x i и прибыли A i . Затем для каждого из четырех проектов построим средствами MS Excel графическую зависимость прибыли А от шага тренда ( t = 1, 2, 3, 4, 5 , 6 ). Активизируем точки графика, щелкнув по ним левой клавишей мыши, затем нажмем правую клавишу и выберем режим «Добавить линию тренда» . Для всех четырех проектов наилучшим типом является полиномиальный 5 -о й степени. С помощью полученных уравнений трендов находим теоретические значения прибыли при различных значениях шага тренда t i . Уравнения моделей тренда, коэффициенты аппроксимации и теоретические значения при были, представлены на рисунке 1.

Рис. 1. Графические зависимости прибыли от вложений и полиномиальные тренды этих зависимостей.

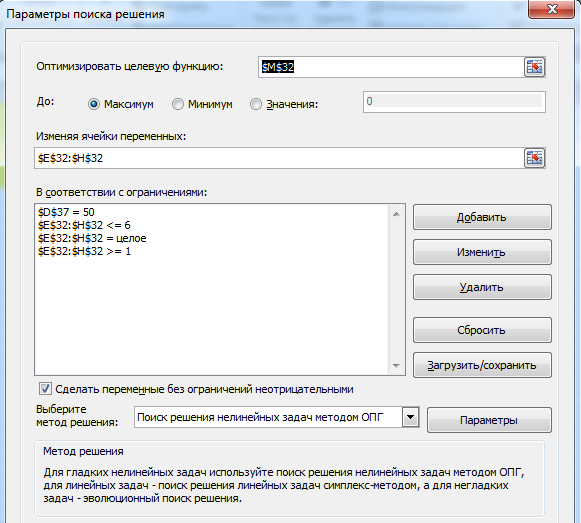
В ячейку М32 вводим выражение для общей (суммарной) прибыли, которую надо максимизировать, — это сумма всех четырех полиномиальных функций. Зависимыми переменными в этой функции являются искомые значения шагов тренда, которые будут располагаться в ячейках E 32 — H 32 . Суммарные вложения не должны превышать 5 0 тыс. ед., следовательно, вводим ограничение 1 0 *(E32+F32+G32 +H32 -4) в ячейку D 37 .

Выбираем из главного меню MS Excel режим «Поиск решения» и заполним открывшееся диалоговое окно в соответствии с требованиями. Нажмем клавишу «выполнить» и получим результат оптимизации.

Рис. 2. Модель максимизации прибыли.

Рис. 3. Оптимальное распределение капиталовложений между проектами.

Имя файла: dinprogr.zip

Размер файла: 129.98 Kb

Если закачивание файла не начнется через 10 сек, кликните по этой ссылке

Источник

2.1. задача о распределении инвестиций

2.1. задача о распределении инвестиций

«Условие задачи. В производственное объединение входят три предприятия Пі, ТІ2, Щ. Руководство объединения решило инвестировать в свои предприятия 5 условных денежных единиц (усл. ден. ед.) в общей сумме. Проведенные маркетинговые исследования прогнозируют величину ожидаемой прибыли каждого из предприятий в зависимости от объема инвестированных средств. Эти данные представлены в приведенной ниже таблице. Считается, что при нулевых инвестициях ожидается нулевая прибыль.

Требуется найти такое распределение инвестиций между предприятиями, которое обеспечило бы максимум суммарной ожидаемой прибыли.

Решение. В данной задаче управляемой системой является рассматриваемое производственное объединение, многошаговым процессом — процесс выделения средств предприятиям. Отметим, что структура многошагового процесса в данной задаче определяется не течением времени, а порядком планирования распределения инвестиций. Экономический эффект представляет суммарная величина ожидаемой прибыли, и при этом задача решается на поиск максимума.

Для решения поставленной задачи построим прежде всего ее экономико-математическую модель в соответствии с пп. 1-5 разд. 1.7 гл. 1.

Число шагов ./V в данной задаче следует принять равным 3, соответствующим числу входящих в производственное объединение предприятий: на первом шаге планируется выделение средств предприятию П, на втором шаге — предприятию Я2, на третьем шаге — предприятию Щ.

В качестве фазовой переменной х, определяющей состояние системы в ходе процесса распределения инвестиций, примем суммарный объем средств, выделенных предприятиям после каждого шага процесса. Именно, переменная х представляет объем средств, выделенных предприятиям после первого шага процесса (т. е. только предприятию П), Х2 — объем средств, выделенных после второго шага (предприятиям П и Д2), х3 —объем средств, выделенных после третьего шага процесса (всем предприятиям П, Я2 и Яз). Поскольку в начальный момент общая сумма выделенных средств равна 0, то начальное состояние системы характеризуется значением xq = 0. По условию задачи общая сумма инвестируемых средств равна 5 усл. ден. ед., т. е. обязательно выполняется условие хз = 5. Поскольку по смыслу задачи на каждом шаге процесса значения фазовой переменной не убывают, то выполняется ограничение Zj ^ 5. Отметим, что проведенный выбор фазовой переменной с указанным экономическим смыслом не является единственно возможным. Например, в рассматриваемой задаче можно было выбрать в качестве переменной х остаток нераспределенных средств.

В качестве управляющей переменной и примем объем средств, выделяемых предприятиям на каждом из шагов процесса. Именно, переменная щ представляет объем средств, выделяемых предприятию Щ (на 1-м шаге процесса), и2 — объем средств, выделяемых предприятию П2 (на 2-м шаге), из — объем средств, выделяемых предприятию 773 (на 3-м шаге). Будем считать, что средства предприятиям выделяются суммами но целому числу усл. ден. ед.; соответственно все управления принимают только целочисленные значения 0, 1, 2. .

Функция процесса хі = /і(хі-і,щ), определяющая закон изменения состояния системы, для данной задачи представляется формулой

и имеет следующий простой смысл: суммарный объем средств хі, выделенных предприятиям нарастающим итогом после текущего шага с номером г, равен суммарному объему средств выделенных предприятиям после предшествующего шага с номером і — 1 (или, что то же самое, до текущего шага), плюс объем средств щ, выделенных предприятию Щ на текущем шаге.

Функция Zi, определяющая частный экономический эффект на шаге с номером г процесса, зависит только от объема щ инвестированных средств в предприятие Щ, т. е. Zi = Zi(m), и определяется по таблице данных задачи по столбцу, отвечающему этому предприятию. Например, z(2) = 4 (из столбца, отвечающего предприятию Пі), z2(3) = 6, 23 (4) = 9.

На этом действия, предписываемые пп. 1-5 разд. 1.7 гл. 1 выполнены, что означает завершение математической формализации поставленной задачи, т. е. построение соответствующей экономико-математической модели. Заметим, что после проведенной указанным образом формализации основные допущения метода ДП выполняются: отсутствие последействия следует из явных формул для вычисления Хі и Zi, а аддитивность целевой функции

Z = Zi(ui) + Z2 (и2) + 23(м3)

обусловлена самой постановкой задачи.

Тем самым можно непосредственно приступить к расчетам в соответствии с методом ДП. Эти расчеты, как указывалось выше в разд. 1.6 гл. 1, проводятся в три этапа: предварительный этап, этап условной оптимизации и этап безусловной оптимизации. На предварительном этапе и на этапе условной оптимизации результаты расчетов заносятся во вспомогательную и основную таблицы той структуры, которая приведена в разд. 1.7 гл. 1. На этапе безусловной оптимизации строится оптимальное решение задачи с использованием информации, содержащейся в основных таблицах.

Предварительный этап. Данный этап решения задачи проводится в естественном порядке для і = 1, 2,3 и не связан непосредственно с вычислением функций Беллмана Ві(хі). Заполняются только первая строка вспомогательной таблицы и четыре левых столбца основной таблицы.

Вспомогательная таблица заполняется соответственно начальному условию xq = 0 и имеет вид

Заполнение основной таблицы проводится следующим образом. Для заданного единственного допустимого значения xq = 0 выбираем все возможные значения управления щ (оно может принимать все целочисленные значения от 0 до 5 включительно) и заносим их во второй столбец таблицы. По формуле xi — xq + щ (следующей из общей формулы хг = Xi-i + щ при і = 1) проводим расчет соответствующих значений переменной хх и заносим их в третий столбец. Для заполнения четвертого столбца значения ожидаемой прибыли zx берем из столбца таблицы исходных данных задачи, отвечающего предприятию Пі. для щ — 1 по этой таблице zj = 2, для и = 2 по таблице zi — 4 и т. д. Для щ = 0 по условию задачи zi = 0. Получаем следующую основную таблицу:

Источник

2.2. задача о распределении инвестиций по максимуму нормы прибыли

2.2. задача о распределении инвестиций по максимуму нормы прибыли

Условие задачи. Сохраняя исходные данные предыдущей задачи, предположим, что руководство производственного объединения имеет возможность инвестировать в свои предприятия не ровно 5 усл. ден. ед., а некоторую сумму от 3 до 5 усл. ден. ед. включительно. Требуется найти такое распределение инвестиций между предприятиями, которое обеспечило бы для производственного объединения максимальную норму прибыли, под которой будем понимать отношение ожидаемой прибыли к объему инвестированных средств.

Замечание 1. Конечно, поставленную задачу можно решить по образцу предыдущей, проведя отдельно расчеты для сумм в 3, 4 и 5 усл. ден. ед., но это привело бы к громоздким дублирующимся вычислениям. Гораздо более эффективным решением будет проведение одного общего расчета по следующей схеме, в которой проведен иной выбор фазовой переменной.

Решение. В данной задаче, как и в предыдущей, управляемой системой является рассматриваемое производственное объединение, многошаговым процессом — процесс выделения средств предприятиям. Экономический эффект представляет норма прибыли, и при этом задача решается на поиск максимума.

Проведем прежде всего математическую формализацию поставленной задачи, т. е. построим ее экономико-математическую модель в соответствии с пп. 1-5 из разд. 1.7 гл. 1.

Число шагов N в данной задаче, как и в предыдущей, следует принять равным 3: на первом шаге планируется выделение средств предприятию Пі, на втором шаге — предприятию П2, на третьем шаге — предприятию Щ.

Поскольку в отличие от предыдущей задачи сумма распределяемых средств не является известной заранее, то следует рассмотреть не одно, а несколько возможных начальных состояний системы. При этом в качестве фазовой переменной х, определяющей состояние системы в ходе процесса распределения инвестиций, удобно принять суммарный объем средств, оставшихся нераспределенными после каждого шага процесса. Начальное состояние системы представляет собой весь объем инвестируемых средств и характеризуется переменной xq, которая может принимать значения 3, 4, 5. Переменная xi представляет объем нераспределенных средств после первого шага процесса (т. е. после выделения средств предприятию Пі), х2 — объем нераспределенных средств после второго шага (после выделения средств предприятиям Пі и П2), 2:3 — объем нераспределенных средств после третьего шага процесса (после выделения средств всем предприятиям Пі, П2 и /7з). Поскольку все инвестируемые средства распределяются между предприятиями без остатка, то должно выполняться условие х\% = 0.

В качестве управляющей переменной и примем, как и в предыдущей задаче, объем средств, выделяемых предприятиям на каждом из шагов процесса. Именно, переменная щ представляет объем средств, выделяемых предприятию Щ на шаге с номером і процесса. Как и выше, будем считать, что средства предприятиям выделяются суммами по целому числу усл. ден. ед., т. е. все управления принимают только целочисленные значения. По смыслу задачи выполняется условие

Функция процесса хі = /і(хі-і,щ), определяющая закон изменения состояния системы, для данного выбора фазовой и управляющей переменных представляется формулой

и имеет следующий экономический смысл: на каждом шаге объем нераспределенных средств уменьшается на величину инвестиций в соответствующее предприятие.

5. Составим целевую функцию, определяющую экономический эффект в данной задаче. Чтобы в наибольшей степени сохранить сходство с предыдущей задачей и подчеркнуть отличия, обозначим частные целевые функции, итоговую целевую функцию и оптимальное значение данной задачи через yi, Y и Y* соответственно. Как и выше, будем обозначать через Zi — Zj(uj) ожидаемую прибыль предприятия И при инвестировании в него средств в объеме щ; эта функция задается таблицей исходных данных из условия предыдущей задачи. Суммарная прибыль производственного объединения равна

и зависит как от общего объема х$ инвестируемых средств, так и от распределения этих средств между предприятиями, т. е. от значений иі,и2,щ. Норма прибыли, которая и является критерием оптимальности Y для рассматриваемой задачи, в соответствии с данным выше определением вычисляется по формуле

при этом, очевидно, частные целевые функции у і следует принять равными Zi/xQ, что приведет к равенству Y = yi + у2 + уз.

Задание аддитивного критерия оптимальности позволяет непосредственно приступить к решению задачи, но мы проведем сначала некоторые преобразования, имея в виду следующие обстоятельства. В выражении для функции Y присутствует деление на переменную xq, имеющую общее значение для всех шагов; возникает желание «вынести» эту переменную «за «скобки». Более того, деление, как правило, приводит к возникновению дробных чисел на промежуточных этапах и загромождает решение.

Попытаемся упростить вычисления за счет незначительного усложнения логики решения задачи следующим образом. Определим функцию Р(хо) как максимальную суммарную прибыль предприятий при равном хо общем объеме инвестиций:

где максимум берется по всевозможным значениям управляющих переменных иі,и2,щ, удовлетворяющим условию щ + и2 + Щ = Xq.

Вычисление функции Р(хо) может быть проведено методом ДП, причем частными целевыми функциями здесь являются Zi, а промежуточные деления отсутствуют. Отношение

равно максимальной норме прибыли производственного объединения при общем объеме хо инвестиций, а оптимальное значение задачи Y* вычисляется по формуле

Щ + U2 + Щ — x0 J = Щ +U2 +Щ = x0

где максимум берется по xq= 3, 4, 5. Проведенные рассуждения можно представить следующей цепочкой равенств:

[_ Xoui,u2,u3 ) x0 ^ Xo )

приводящей, естественно, к тому же результату. Таким образом, решение задачи может быть проведено по следующей схеме:

вычисление функции Р(хо) для каждого допустимого значения жо методом ДП;

вычисление оптимального значения задачи Y* и построение оптимального решения.

На этом математическая формализация поставленной задачи завершена. Как нетрудно проверить, основные допущения метода ДП — отсутствие последействия и аддитивность целевой функции —для нее выполняются. Тем самым можно непосредственно приступить к расчетам, включающим предварительный этап, этап условной оптимизации и этап безусловной оптимизации. Важно подчеркнуть, что вычисляемая функция Р(хо) равна функции Беллмана Во(хо) для решаемой задачи с целевой функцией 21+22 + 23:

При оформлении решения данной задачи (в отличие от предыдущей) во избежание громоздких повторений таблиц все получаемые при решении таблицы приведены сразу окончательно заполненными.

Предварительный этап. Данный этап решения задачи проводится в естественном порядке для г = 1, 2, 3 и не связан непосредственно

Источник