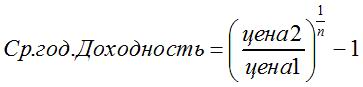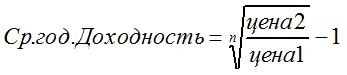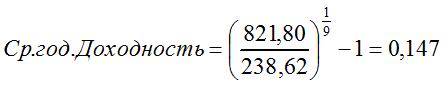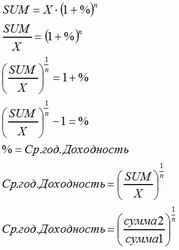Что такое средний уровень доходности

Как рассчитать среднюю (среднегодовую) доходность?

Показатель среднегодовой (средней) доходности вложения бывает интересен инвестору во многих случаях. В частности, для правильной оценки перспектив вложения на длительный срок, сравнения средней доходности различных инструментов вложений или определения и сравнения годовых уровней инфляции.

В качестве исходных данных для его расчета нужно иметь информацию относительно общей доходности актива или, по крайней мере, знать начальную и конечную цену продукта. Также следует определиться с временным периодом вычисления средней доходности.

Пример расчета среднегодовой доходности

Итак, наши исходные данные таковы:

• Период: девять лет;
• Начальная цена (31.12.1999 г.): 238,62 руб.;
• Конечная цена (31.12.2008 г.): 821,80 руб.

Среднегодовая доходность считается как отношение конечной цены к начальной, возведенное в степень 1/n минус 1. Здесь n — период (количество лет).

В другом виде эта формула записывается как корень n-ной степени из отношения конечной цены к начальной минус 1.

Обычно доходность (не путайте, кстати, с доходом) измеряют в процентах, поэтому полученное значение умножаем на 100% и получаем конечную величину среднегодовой доходности золота за требуемый период — 14,7%.

Некоторая математическая сложность формулы расчета среднегодовой доходности связана с формулой расчета сложных процентов. Обоснование ее правильности доступно каждому, владеющими основами высшей математики. Непосвященных в таинства вышмата могут ознакомится с выкладками на рисунке, приведенным ниже:

Используя приведенные формулу, можно произвести расчеты среднегодовой доходности любого финансового инструмента. Для этого может подойти и обычный калькулятор, но удобнее всего воспользоваться программой EXEL и ее функцией «Формула СТЕПЕНЬ». В этом случае достаточно войти в EXEL и набрать строку:

Судя по их контенту, этому тексту релевантны статьи:

В чем хранить деньги в 2012 году Как сохранить деньги? Иногда вопрос о том, как сохранить свои сбережения, становится так же остро, как и вопрос, как заработать деньги. Совершить удачное капиталовложение в виде покупки недвижимости или автомобиля — решение неплохое, но наличные, обладающие высокой степенью ликвидности в любой ситуации, тоже нужно иметь в достаточном количестве.

Самой дорогой монетой является американский « Двойной Орел » номиналом в $20. Монета чеканки 1933 была продана за 7 590 020 $, и всего было отчеканено 445 000 таких монет. На аверсе монеты (лицевой стороне) — изображение Свободы…

Знаменитый американский финансист Джордж Сорос родился 12 августа 1930 года, в столице Венгрии – Будапеште. За свою жизнь пройдя «огонь и воду», Джордж добился огромных успехов. Один из богатейших людей Америки, сторонник открытого общества и социальных взглядов.

Источник

Курс лекций «Основы финансового менеджмента»

5.2. Определение средней доходности

В практике финансовых расчетов часто возникает необходимость расчета средней доходности набора (портфеля) инвестиций за определенный период или средней доходности вложения капитала за несколько периодов времени (например, 3 квартала или 5 лет). В первом случае используется формула среднеарифметической взвешенной , в которой в качестве весов используются суммы инвестиций каждого вида. Вернемся к примеру из предыдущего параграфа с вложением 1000 рублей в два вида деятельности: торговую и финансовую. Можно сказать, что владелец этих денег сформировал инвестиционный портфель, состоящий из двух инструментов – инвестиции в собственный капитал магазина и финансовые (спекулятивные) инвестиции. Сумма каждого из вложений составила 500 рублей. Доходность по первому направлению вложений составила 10%, по второму – 40% годовых. Применив формулу средней арифметической (в данном случае, ввиду равенства весов, можно использовать среднюю арифметическую простую) получим среднюю доходность инвестиций за год, равную 25% ((10 + 40) / 2). Она в точности соответствует полной доходности “портфеля”, рассчитанной в предыдущем параграфе. Если бы владелец изменил структуру своих инвестиций и вложил в торговлю только 300 рублей (30%), а в финансовые спекуляции 700 рублей (70%), то при неизменных уровнях доходности каждого из направлений средняя доходность его “портфеля” составила бы 31% (10 * 0,3 + 40 * 0,7). Следовательно, общую формулу расчета средней доходности инвестиционного портфеля можно представить следующим образом:

, где (5.2.1)

n – число видов финансовых инструментов в портфеле;

r i – доходность i -го инструмента;

w i – доля (удельный вес) стоимости i -го инструмента в общей стоимости портфеля на начало периода.

Реальный срок вложения капитала может принимать любые значения – от одного дня до многих лет. Для обеспечения сопоставимости показателей доходности по инвестициям различной продолжительности эти показатели приводятся к единой временной базе – году (аннуилизируются). Методика аннуилизации доходности была рассмотрена в предыдущем параграфе. Однако, годовая доходность одних и тех же инвестиций может быть неодинаковой в различные промежутки времени. Например, доходность владения финансовым инструментом (за счет прироста его рыночной цены) составила за год 12%. В течение второго года цена увеличилась еще на 15%, а в течение третьего – на 10%. Возникает вопрос: чему равна средняя годовая доходность владения инструментом за 3 года? Так как годовая доходность суть процентная ставка, средняя доходность за период рассчитывается по формулам средних процентных ставок. В зависимости от вида процентной ставки (простая или сложная) ее средняя величина может определяться как среднеарифметическая, взвешенная по длительности периодов, в течение которых она оставалась неизменной, или как среднегеометрическая , взвешенная таким же образом (см. § 2.2).

В принципе возможно применение обоих способов для определения средней за несколько периодов доходности. Например, среднеарифметическая доходность инструмента, о котором говорилось выше, составит за три года 12,33% ((12 + 15 + 10) / 3). В данном случае продолжительность периодов, в течение которых доходность оставалась неизменной (год), не менялась, поэтому используется формула простой средней. Применив формулу средней геометрической, получим r ср = 12,315% (((1 + 0,12) * (1 + 0,15) * (1 + 0,1)) 1/3 -1). При незначительной разнице в результатах, техника вычисления среднеарифметической доходности значительно проще, чем среднегеометрической, поэтому довольно часто используется более простой способ расчета.

Однако при этом допускается существенная методическая ошибка : игнорируется цепной характер изменения доходности от периода к периоду. Доходность 12% была рассчитана к объему инвестиций на начало первого года, а доходность 15% — к их величине на начало следующего года. Эти величины не равны друг другу, так как в течение первого года инвестиции подорожали на 12%. За второй год они стали дороже еще на 15%, то есть их объем на начало третьего года также отличался от двух предыдущих сумм. Применяя формулу средней арифметической, молчаливо предполагают, что объем инвестиций оставался неизменным в течение всех периодов, то есть по сути рассчитывается средний базисный темп прироста. В данном случае это предположение совершенно неверно, поэтому следует рассчитывать средний цепной темп прироста по формуле средней геометрической, так как начальная сумма инвестиций меняется от периода к периоду. Представим исходные данные примера в табличной форме (табл. 5.2.1).

Таблица 5.2.1
Динамика доходности акции за 3 года
руб.

Источник

Зачем рассчитывать рентабельность

Рентабельность — это экономический показатель, который показывает, насколько эффективно используются ресурсы: сырье, кадры, деньги и другие материальные и нематериальные активы. Можно рассчитать рентабельность отдельного актива, а можно — всей компании сразу.

Рентабельность рассчитывают, чтобы спрогнозировать прибыль, сравнить компанию с конкурентами или предсказать доходность инвестиций. Еще рентабельность предприятия оценивают, если собрались его продавать: компания, которая приносит больше прибыли и при этом тратит меньше ресурсов, стоит дороже.

Как рассчитывается рентабельность

Существует коэффициент рентабельности — он показывает, насколько эффективно используются ресурсы. Этот коэффициент — это отношение прибыли к ресурсам, которые вложили, чтобы ее получить. Коэффициент может выражаться в конкретной величине прибыли, полученной на единицу вложенного ресурса, а может — в процентах.

Например, компания производит сметану. 1 литр молока стоит 5 рублей, а 1 литр сметаны — 80 рублей. Из 10 литров молока получается 1 литр сметаны. Из 1 литра молока можно сделать 100 миллилитров сметаны, которые будут стоить 8 рублей. Соответственно, прибыль с 1 литра молока — 3 рубля ( 8 Р − 5 Р ).

Чтобы посчитать рентабельность ресурса «Молоко», делим прибыль на стоимость ресурса: 3 / 5 = 0,6 , или 60%.

А другая компания производит мороженое. 1 килограмм мороженого стоит 200 рублей. Для его производства надо 20 литров молока по той же цене — 5 рублей за литр. Из 1 литра молока получится 50 граммов мороженого, которые будут стоить 10 рублей. Прибыль с 1 литра молока — 5 рублей ( 10 Р − 5 Р ).

Рентабельность ресурса «Молоко» при производстве мороженого: 5 / 5 = 1 , или 100%.

Вывод: отдача от ресурсов при производстве мороженого выше, чем при производстве сметаны, — 100% > 60%.

Коэффициент рентабельности может выражаться также в количестве затраченных ресурсов, которые понадобились, чтобы получить фиксированную сумму прибыли. Например, чтобы получить 1 рубль прибыли в случае со сметаной, надо потратить 330 миллилитров молока. А в случае с мороженым — 200 миллилитров.

Виды показателей рентабельности

Чтобы оценить эффективность работы компании, используют несколько показателей рентабельности. Каждый из них рассчитывается как отношение чистой прибыли к какой-то величине:

1. К активам — рентабельность активов (ROA).
2. К выручке — рентабельность продаж (ROS).
3. К основным средствам — рентабельность основных средств (ROFA).
4. К вложенным деньгам — рентабельность инвестиций (ROI).
5. К собственному капиталу — рентабельность собственного капитала (ROE).

Проще говоря, показатель рентабельности — это прибыль, которую делят на тот показатель, рентабельность которого хотят узнать.

Порог рентабельности

Порог рентабельности — это минимальная прибыль, которая покрывает затраты. Например, вложения, если речь идет об инвестициях, или себестоимость — если о производстве продукции. Когда говорят о пороге рентабельности, чаще всего используют термин «точка безубыточности».

Рентабельность активов (ROA)

Показатель ROA рассчитывают, чтобы понять, насколько эффективно используются активы компании — здания, оборудование, сырье, деньги — и какую в итоге они приносят прибыль. Если рентабельность активов ниже нуля, значит, предприятие работает в убыток. Чем выше ROA, тем эффективнее организация использует свои ресурсы.

Как рассчитать рентабельность активов. Это отношение чистой прибыли за определенный период к стоимости активов.

ROA = П / ЦА × 100%,

П — прибыль за период работы;

ЦА — средняя цена активов, которые находились на балансе в это же время.

Рентабельность продаж (ROS)

Рентабельность продаж показывает долю чистой прибыли в общей выручке предприятия. При расчете коэффициента вместо чистой прибыли также может использоваться валовая прибыль или прибыль до уплаты налогов и процентов по кредитам. Называться такие показатели будут соответственно — коэффициент рентабельности продаж по валовой прибыли и коэффициент операционной рентабельности.

Как рассчитать рентабельность продаж. ROS рассчитывают как отношение прибыли к выручке.

Рентабельность основных производственных фондов (ROFA)

Основные производственные фонды — активы, которые организация использует для производства товаров или услуг и которые при этом не расходуются, а только изнашиваются. Например, здания, оборудование, электрические сети, автомобили и т. п. ROFA показывает доходность от использования основных средств, которые участвуют в производстве продукта или услуги.

Как рассчитать рентабельность основных производственных фондов. Это отношение чистой прибыли к стоимости основных средств.

ROFA = П / Цс × 100%,

П — чистая прибыль организации за нужный период;

Цс — стоимость основных средств компании.

Рентабельность оборотных активов (RCA)

Оборотные активы — это ресурсы, которые используются компанией для производства товаров и услуг, но которые, в отличие от основных фондов, полностью расходуются. К оборотным активам относят, например, деньги на счетах предприятия, сырье, готовую продукцию на складе и т. п. RCA показывает эффективность управления оборотными активами.

Как рассчитать рентабельность оборотных активов. Это отношение чистой прибыли к оборотным средствам.

RCA = П / Цо × 100%,

П — чистая прибыль за определенный период;

Цо — стоимость оборотных активов, которые использовали для производства товара или услуги за это же время.

Рентабельность капитала (ROE)

ROE показывает, с какой отдачей работают деньги, вложенные в компанию. Причем вложения — это только уставный или акционерный капитал. Чтобы рассчитать эффективность использования не только собственных, но и привлеченных средств, используют показатель рентабельности задействованного капитала — ROCE. Он дает понять, какой доход приносит компания. Рентабельность капитала сравнивают не только с аналогичными показателями других компаний, но и с другими видами инвестиций. Например, с процентами по банковским вкладам, чтобы понять, есть ли смысл инвестировать в бизнес.

Как рассчитать рентабельность капитала. Это отношение чистой прибыли к капиталу компании, включая резервы.

Источник

Средняя доходность

Что такое Средняя доходность?

Средняя доходность – это простое математическое среднее ряда доходностей, генерируемых за определенный период времени. Средняя доходность рассчитывается так же, как и простое среднее значение для любого набора чисел. Числа складываются в одну сумму, а затем сумма делится на количество чисел в наборе.

Формула средней доходности

Как рассчитать средний доход

Существует несколько показателей доходности и способов их вычисления, но для средней арифметической доходности нужно взять сумму доходности и разделить ее на количество цифр доходности.

Что вам говорит средний доход?

Средняя доходность сообщает инвестору или аналитику, какова была доходность акций или ценных бумаг в прошлом или какова доходность портфеля компаний. Это не то же самое, что годовая доходность. Средняя доходность не учитывает начисление процентов.

Ключевые моменты

• Средняя доходность – это простое математическое среднее ряда доходностей.
• Это может помочь измерить прошлую доходность ценной бумаги или доходность портфеля.
• Среднее геометрическое всегда ниже средней доходности.

Пример использования средней доходности

Одним из примеров средней доходности является простое среднее арифметическое . Например, предположим, что инвестиции приносят следующую прибыль ежегодно в течение пяти полных лет: 10%, 15%, 10%, 0% и 5%. Чтобы рассчитать среднюю доходность инвестиций за этот пятилетний период, пять годовых доходов складываются и затем делятся на 5. Это дает среднегодовую доходность 8%.

Или рассмотрим Wal-Mart (NYSE: WMT). Акции Wal-Mart вернулись на 9,1% в 2014 году, потеряли 28,6% в 2015 году, выросли на 12,8% в 2016 году, выросли на 42,9% в 2017 году и потеряли 5,7% в 2018 году. Средняя доходность Wal-Mart за эти пять лет составляет 6,1% или 30,5%, разделенные на 5 лет.

Расчет прибыли от роста

Простой темп роста является функцией начальных и конечных значений или остатков. Он рассчитывается путем вычитания конечного значения из начального значения и последующего деления на начальное значение. Формула выглядит следующим образом:

Например, если вы инвестируете 10 000 долларов в компанию, а цена акций увеличивается с 50 до 100 долларов, прибыль можно рассчитать, взяв разницу между 100 и 50 долларами и разделив ее на 50 долларов. Ответ – 100 процентов, что означает, что теперь у вас есть 20 000 долларов.

Разница между средней доходностью и геометрической средней

Если смотреть на среднюю историческую доходность, среднее геометрическое является более точным расчетом. Среднее геометрическое всегда ниже средней доходности. Одним из преимуществ использования среднего геометрического является то, что не требуется знать фактические инвестированные суммы. расчет полностью сосредоточен на самих цифрах доходности и представляет собой сравнение «яблок с яблоками» при рассмотрении результатов двух или более инвестиций за более различные периоды времени.

Среднюю геометрическую доходность иногда называют взвешенной по времени ставкой доходности (TWRR), поскольку она устраняет искажающее влияние на темпы роста, создаваемое различными притоками и оттоками денег на счет с течением времени.

В качестве альтернативы, взвешенная по денежным средствам ставка доходности (MWRR) включает размер и сроки денежных потоков, поэтому она является эффективной мерой для доходности портфеля, который получил депозиты, реинвестирование дивидендов, выплату процентов или снятие средств. Доходность, взвешенная по деньгам, эквивалентна внутренней норме прибыли, где чистая приведенная стоимость равна нулю.

Ограничения использования средней доходности

Простое среднее значение доходности – это простой расчет, но он не очень точный. Для более точных расчетов доходности аналитики и инвесторы также часто используют среднее геометрическое или доходность, взвешенную по деньгам.

Источник