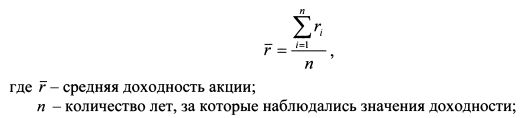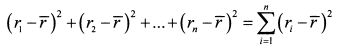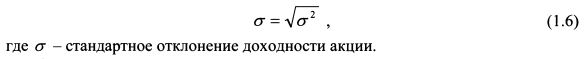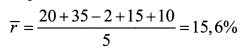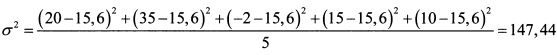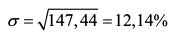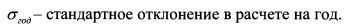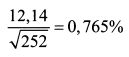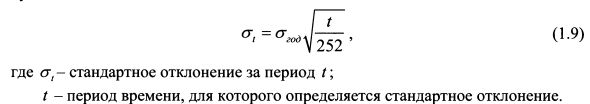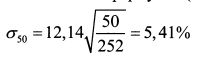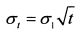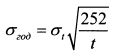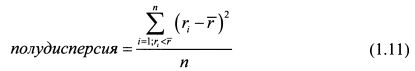Чему равна ожидаемая доходность дисперсия

Дисперсия (вариация) | Variance

В статистике дисперсия или вариация (англ. Variance) является показателем, который используется для оценки разброса значений случайной величины относительно ее математического ожидания. В портфельной теории дисперсия доходности является мерой риска, связанного с инвестированием в определенный актив или портфель активов.

Формула

Если известен полный набор вероятностей исхода события, что крайне редко встречается на практике, для расчета величины дисперсии используется следующая формула:

где k_i – доходность ценной бумаги или актива при i-ом варианте исхода событий;

— ожидаемая доходность ценной бумаги или актива;

p_i – вероятность i-го варианта исхода событий.

В реальной практике инвестирования аналитику обычно доступны исторические данные о доходности ценной бумаги или актива. Если он располагает всем массивом информации, то есть оценивает дисперсию на основании генеральной совокупности данных, необходимо использовать следующую формулу:

где k_i – i-ое значение доходности ценной бумаги;

— средняя доходность ценной бумаги;

n – количество наблюдений.

Однако чаще оценку риска проводят на основании некоторой выборки из генеральной совокупности данных, поэтому для получения несмещенной оценки дисперсии количество степеней свободы уменьшают на 1. В этом случае формула для ее оценки будет выглядеть следующим образом:

Интерпретации дисперсии

Чем выше значение дисперсии, то есть чем выше разброс доходности актива или портфеля активов относительно его ожидаемой доходности, тем выше будет уровень риска. Напротив, низкие значения этого показателя свидетельствуют о низком уровне риска, связанного с осуществлением инвестиций.

Также следует отметить, что квадратный корень от дисперсии случайной величины является ее среднеквадратическим отклонением.

Пример расчета

Пример 1. Предположим, что финансовому аналитику необходимо произвести оценку риска, связанного с приобретением акций Компании А и Компании Б. Предположим, что аналитику известен полный набор вероятностей событий, который представлен в таблице.

Ожидаемая доходность для акций Компании составит 18,75%, а для акций Компании Б 19,45%.

_А = 7*0,05+15*0,2+18*0,5+24*0,2+32*0,05 = 18,75%

_Б = -24*0,05+8*0,2+20*0,5+31*0,2+57*0,05 = 19,45%

В свою очередь, дисперсия доходности акций Компании А будет равна 24,288%, а акций Компании Б 217,948%.

σ 2 _А = (7-18,75)2*0,05 + (15-18,75)2*0,2 + (18-18,75)2*0,5 + (24-18,75)2*0,2 + (32-18,75)2*0,05 = 24,288%

σ 2 _Б = (-24-19,45)2*0,05 + (8-19,45)2*0,2 + (20-19,45)2*0,5 + (31-19,45)2*0,2 + (57-19,45)2*0,05 = 217,948%

Хотя ожидаемая доходность у акций обеих компаний практически одинаковая, риски инвестирования в акции Компании Б будут существенно выше.

Пример 2. Историческая доходность акций за последние пять лет представлена в таблице.

Средняя доходность акции составит 5,784%.

= (5,78+12,33-7,21+8,25+9,77)/5 = 5,784%

Поскольку анализируется не вся генеральная совокупность данных, а только выборку из нее, оценка дисперсии составит 58,42%.

σ 2 = ((5,78-5,784)2 + (12,33-5,784)2 + (-7,21-5,784)2 + (8,25-5,784)2 + (9,77-5,784)2)/(5-1) = 58,42%

Источник

Чему равна ожидаемая доходность дисперсия

Ожидаемая доходность и дисперсия доходности портфеля ценных бумаг

В главах 7, 8 и 9 описан метод формирования оптимального инвестиционного портфеля. В соответствии с ним инвестору необходимо оценивать ожидаемые доходности и дисперсии всех рассматриваемых ценных бумаг. Более того, должны быть оценены все ковариации этих ценных бумаг и определена безрисковая процентная ставка. И лишь после того, как все это проделано, инвестор может определить структуру касательного портфеля, а также ожидаемую доходность и среднеквадратичное отклонение. На следующем этапе инвестор может перейти к определению оптимального портфеля, отмечая на графике те точки, где одна из кривых безразличия касается, но не пересекает эффективное множество. И так как эффективное множество представляет собой прямую, то оптимальный портфель включает инвестиции в касательный портфель, комбинированные с определенным количеством безрисковых вложений и кредитов. [c.258]

ОЖИДАЕМАЯ ДОХОДНОСТЬ И ДИСПЕРСИЯ ДОХОДНОСТИ ПОРТФЕЛЯ ЦЕННЫХ БУМАГ [c.71]

Как было показано в гл. 2, если коэффициент корреляции в парах активов меньше чем 1,0, то диверсификация может улучшить взаимосвязь между ожидаемым риском портфеля и ожидаемым доходом по портфелю. Это происходит потому, что, если переменная доходности является линейной функцией средней доходности, то фактор риска представляет собой квадратическую функцию дисперсии доходов по ценным бумагам. Степень улучшения портфеля зависит от весов, которые каждый из активов имеет в портфеле, и от корреляции этих активов. [c.442]

Последние две формулы весьма полезны при расчетах ожидаемой доходности и дисперсии портфеля ценных бумаг. [c.49]

Рассмотрим простейшую модель выбора оптимального портфеля ценных бумаг. Условно разделим все финансовые активы на две группы. К первой группе отнесем безрисковые активы. Такие активы обладают очень низкой ожидаемой доходностью, и мы будем считать, что их ожидаемая доходность равна нулю. Эту группу активов мы и будем называть деньгами. Обозначив ожидаемую доходность через ге, а риск (который измеряется как корень из дисперсии, то есть, среднеквадратическое отклонение) через а мы можем дать характеристику первого актива (денег) г = 0, 0, 0. Обозначим через а (0

Источник

Ожидаемая доходность акций

В сфере инвестирования ожидаемая доходность (англ. Expected Rate of Return) представляет собой процентную ставку или сумму, которую инвестор ожидает получить в течение определенного периода времени от вложений в определенный актив. С практической точки зрения этот показатель может быть рассчитан исходя из полного набора вероятностей, либо на основе исторических данных о доходности актива.

Формула

В случае, если заранее известен полный набор вероятностей, то есть вероятности всех возможных вариантов исхода событий, ожидаемую доходность можно рассчитать использовав следующую формулу:

(1)

где P_i – вероятность наступления i-го исхода событий;

k_i – доходность при i-ом исходе событий;

n – количество исходов событий.

В условиях реального финансового рынка инвестор, как правило, принимает решение на основании имеющейся информации об исторической доходности ценной бумаги. В этом случае ожидаемая доходность рассчитывается как среднеарифметическое:

(2)

k_i – доходность ценной бумаги в i-ом периоде;

n – количество наблюдений.

Пример расчета

Пример 1. Финансовый аналитик рассматривает возможность включения в портфель инвестора одной дополнительной акции, выбирая из трех компаний, работающих в сфере оптово-розничной торговли. При этом он рассматривает три возможных сценария развития событий, вероятность и предполагаемая доходность которых представлены в таблице.

Чтобы определить ожидаемую доходность каждой из ценных бумаг, необходимо воспользоваться первой из приведенных выше формулой. Для акций Компании А она составит 11,25%, акций Компании Б 12,4% и акций Компании В 12,9%.

_А = 0,25*18+0,5*12+0,25*3 = 11,25%

_Б = 0,3*22+0,45*14+0,25*(-2) = 12,4%

_В = 0,2*35+0,45*17+0,35*(-5) = 12,9%

Если не принимать во внимание прочие факторы (например, риск), то в портфель инвестора целесообразно включить акции Компании В, поскольку они характеризуются самой высокой ожидаемой доходностью.

Пример 2. Финансовому аналитику необходимо оценить ожидаемую доходность акций на основании данных об их исторической доходности за последние 7 недель, которые представлены в таблице.

Поскольку аналитику известна только историческая доходность акций, необходимо воспользоваться второй из приведенных выше формул.

_А = (-2,3+7+4,1-3,4+6,2+4,5+1,8)/7 = 2,56%

_Б = (4,1-5,7+2,4+4,8-1,2+1,1+0,3)/7 = 0,83%

_В = 0,2*35+0,45*17+0,35*(-5) = 0,64%

Источник

1.2. Ожидаемый риск портфеля. 1.2.1. Риск актива

Основополагающими мерами риска финансового актива являются такие показатели как стандартное отклонение и дисперсия его доходности. В качестве синонима понятия стандартное отклонение используют также термин «волатильность». Стандартное отклонение и дисперсия доходности актива говорят о степени возможного разброса его фактической доходности вокруг его средней доходности. Данные меры риска можно определить на основе прошлых данных статистики доходности актива. Рассмотрим технику определения дисперсии и стандартного отклонения доходности на примере акции.

Пусть имеются значения доходности акции за п лет. За первый год она составила величину r1, за второй – r2, третий –r3 г3 и т.д., за п-й год – rn. Разобьем расчеты на несколько шагов.

ШАГ 1. Определяем среднее значение доходности акции за п лет. Это просто среднее арифметическое значений ее доходности за этот период:

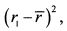
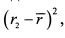
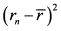
ШАГ 2. Определяем для каждого года отклонение фактического значения доходности от ее средней доходности, и возводим полученные данные в квадрат. Для первого года получаем: для второго года – и т. д., для n-го года – .

ШАГ 3. Суммируем квадраты отклонений:

ШАГ 4. Делим полученную сумму на количество лет:

Величина 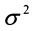является дисперсией доходности акции в расчете на год. Как уже отмечалось, дисперсия является показателем рассеяния фактических значений доходности акции вокруг ее средней доходности. Размерность дисперсии представляет собой квадрат доходности акции. Если в формуле мы учитываем доходность в процентах, то размерность дисперсии – это процент в квадрате. Показателем такой размерности не всегда удобно пользоваться, поскольку сама доходность акции измеряется в процентах. Поэтому из дисперсии извлекают квадратный корень и получают стандартное отклонение доходности:

Стандартное отклонение измеряется уже в процентах, т.е. в тех же единицах, что и сама доходность.

Если предположить, что при расчете дисперсии и стандартного отклонения мы учли все существующие значения доходности, т. е., как говорят, всю генеральную совокупность случайной переменной, то полученная по формуле (1.5) дисперсия называется генеральной дисперсией, а стандартное отклонение в формуле (1.6) – генеральным стандартным отклонением. Однако на практике невозможно учесть все фактические значения доходности акции, так как это непрерывная случайная величина. Поэтому оценку данных показателей проводят на основе только части их значений, т.е. на основе некоторой выборки данных. Тогда в результате расчета по формуле (1.5) получают так называемую выборочную дисперсию.

Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то она будет приводить к систематическим ошибкам, занижая значение генеральной дисперсии. Это происходит потому, что при расчете отклонения его считают не от истинного среднего значения переменной, а от выборочного. Выборочное же среднее непосредственно находится в центре выборки и поэтому отклонения от него выборочных данных в среднем меньше, чем от действительного среднего значения переменной в генеральной совокупности. Чтобы скорректировать данную погрешность переходят к так называемой исправленной дисперсии. Она определяется по формуле:

Формула (1.7) отличается от формулы (1.5) только знаменателем. Данная корректировка осуществляется для того, чтобы получить несмещенную оценку генеральной дисперсии. Корректировка является существенной, если оценку дисперсии проводят на основе небольшого количества данных. При большом объеме выборки различие в расчетах будет незначительным. На практике пользуются исправленной дисперсией, если количество наблюдений примерно меньше 30. Соответственно исправленное стандартное отклонение определяется по формуле:

Определить выборочное стандартное отклонение доходности акции, если ее доходность за первый год составила 20%, второй — 35% , третий — минус 2%, четвертый — 15% , пятый — 10%.

ШАГ 1. Определяем среднюю доходность акции:

ШАГ 2. Определяем дисперсию доходности согласно формуле (1.5):

ШАГ 3. Определяем выборочное стандартное отклонение доходности акции:

Рассматривая технику определения стандартного отклонения и цифровой пример, мы оперировали временным периодом равным году. На практике возникает задача определения стандартного отклонения для других временных периодов.

Если имеется значение стандартного отклонения за год, то для определения его за один день надо стандартное отклонение в расчете на год разделить на корень квадратный из количества торговых дней в году. В году насчитывается порядка 252 дней. Поэтому стандартное отклонение доходности актива за день получим по формуле:

Так, стандартное отклонение доходности акции за один день в приведенном выше примере равно:

Если мы определяем стандартное отклонение за некоторый период на основе годичного стандартного отклонения, то в общем виде формула имеет следующий вид:

Пусть в нашем примере требуется определить стандартное отклонение доходности акции за 50 дней. В соответствии с формулой (1.9) оно составляет:

Если известно стандартное отклонение за один день, то определить его в расчете на год можно по формуле:

Соответственно стандартное отклонение за любой другой период времени (ст,) определяется по формуле:

Получить стандартное отклонение за год на основе его значения за некоторый период t можно с помощью следующей формулы:

На практике волатильность часто определяют на основе данных о ежедневной доходности акции. Доходность акции за один день определяется по формуле:

Показатель rt является первым статистическим наблюдением. Далее берут цену акции при закрытии для дня t2 и определяют аналогичным образом доходность акции за второй день и т.д. На основе полученных данных о ежедневной доходности по формуле стандартного отклонения определяют волатильность в расчете на один день. Затем по формуле (1.10) определяют волатильность в расчете на год. Обычно в литературе показатель стандартного отклонения приводится в расчете на год, если не сказано иное.

Удобство расчета стандартного отклонения на основе ежедневных данных состоит в том, что можно воспользоваться большим количеством наблюдений. В то же время, при определении волатильности за год на основе значения волатильности за день можно допустить существенную погрешность. Она будет особенно велика, если стандартное отклонение актива следует процессу «mean reversion» (возвращение к среднему значению). «Mean reversion» означает, что волатильность актива в долгосрочной перспективе испытывает колебания вокруг некоторого среднего значения, а не возрастает бесконечно пропорционально величине \t .

На практике приемлемый результат получается, если рассчитывать стандартное отклонение для более длительных периодов на основе более коротких, используя период времени до 10 дней. Так, определив волатильность в расчете на день, можно рассчитать волатильность для десятидневного периода, умножив полученную цифру на V10 .

Когда инвестора интересует волатильность за более длительные периоды, можно взять прошлые статистические данные с требуемым интервалом. Например, инвестор определяет волатильность для одного месяца. Тогда необходимо взять наблюдения за предыдущие периоды времени по 30 дней. Причем, чтобы исключить автокорреляцию9, следует использовать не пересекающиеся временные периоды. Неудобство такого подхода при расчете волатильности для больших периодов состоит в том, что приходится использовать наблюдения за несколько предыдущих лет. При определении стандартного отклонения в расчете на месяц хорошую оценку риска можно получить, если учесть помесячные данные доходности за период времени не меньше трех лет.

Доходность актива является случайной величиной и поэтому может принимать различные значения. Если значения переменной изменяются во времени неопределенным образом, то говорят, что она следует стохастическому, т. е. вероятностному процессу. Значения переменной могут изменяться дискретно или непрерывно. В первом случае величина переменной изменяется только на определенную (дискретную) величину, во втором — может принимать любые значения в рамках некоторого диапазона.

Значения одной переменной могут изменяться только в определенные моменты времени, другой — в любое время. Поэтому выделяют соответственно дискретный и непрерывный стохастические процессы.

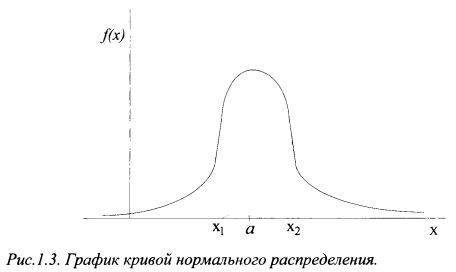
Доходность актива является непрерывной случайной величиной и подчиняется некоторому вероятностному распределению. Наиболее часто в жизни встречается нормальное распределение. Оно возникает в том случае, когда на случайную величину оказывает влияние множество факторов, каждый из которых не имеет определяющего значения. График кривой нормального распределения (его еще называют графиком плотности вероятности) случайной величины приведен на рис. 1.3. По оси абсцисс представлена область возможных значений случайной величины X, по оси ординат — плотность распределения вероятностей случайной величины X. В самом общем виде можно дать следующее определение плотности вероятности: это вероятность, приходящаяся на единицу длины отрезка, на котором может принимать значения случайная величина. Если быть более точным, то она характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке.

Плотность распределения f(x) является одной из форм закона распределения случайной величины, но существует только для непрерывных случайных величин.

График кривой нормального распределения симметричен относительно среднего значения случайной величины, которое называют еще математическим ожиданием случайной величины. На графике точка а является математическим ожиданием случайной величины X. Сама случайная величина может принимать любые отрицательные и положительные значения. Правая и левая ветви графика асимптотически приближаются к оси абсцисс. Вся площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Если нас интересует вероятность попадания случайной величины на какой-либо интервал оси абсцисс, то она будет равна площади фигуры, ограниченной сверху кривой распределения, снизу — осью абсцисс, по бокам — перпендикулярами, проходящими через концы интервала. Так, вероятность попадания случайной величины X на отрезок (х2х<) (см. рис. 1.3) равна площади фигуры, заштрихованной косыми пунктирными линиями. Нормальное распределение полностью определяется двумя характеристиками случайной величины - ее математическим ожиданием и стандартным отклонением. Таким образом, зная математическое ожидание и стандартное отклонение случайной величины, мы имеем полную картину вероятностного распределения ее возможных значений.

Стандартное отклонение характеризует степень рассеяния возможных значений случайной величины вокруг ее среднего значения. Кроме этого, оно говорит о вероятности того, что значение случайной переменной окажется в некотором интервале. Для нормально распределенной случайной величины полезно запомнить так называемое «правило трех сигм». Оно говорит о том, что вероятность получить значение случайной переменной в диапазоне одного стандартного отклонения от ее средней величины равно 68,3%, в диапазоне двух стандартных отклонений — 95,4%, трех стандартных отклонений — 99,7%. Остается еще 0,3% вероятности того, что случайная величина примет любое другое значение, выходящее за рамки отмеченных границ.

Важно: актуальное предложение по поводу компенсации до 100% комиссии, взимаемой Вашим брокером.

Проиллюстрируем данное правило на основе примера по расчету волатильности, который был приведен выше. Среднее значение, т.е. математическое ожидание доходности акции равнялось 15,6%, а стандартное отклонение доходности в расчете на год — 12,14%. Согласно правилу трех сигм, инвестор вправе ожидать, что с вероятностью 68,3% доходность акции через год будет располагаться в интервале от 15,6% ±12,14%, т.е. от 3,46% до 27,74%. С вероятностью 95,4% этот интервал составит 15,6%±2*12,14%, т.е. от -8,68% до 39,88%. С вероятностью 99,7% интервал возможной доходности будет равен 15,6% ±3*12,14% или от -20,82% до 52,02%. Остаются еще 0,3% вероятности того, что акция принесет как гораздо более высокую так и низкую доходность.

Таким образом, стандартное отклонение доходности актива выступает мерой степени и вероятности разброса ее возможных значений вокруг ее средней доходности.

Стандартное отклонение является мерой риска изменения доходности актива. Зная данную величину, инвестор может выбирать между более или менее рискованными бумагами. Например, имеются две акции — А и В. Их средняя доходность одинакова и равна 30%, так как это просто средняя арифметическая их доходностей за определенный период времени. В то же время, стандартное отклонение в расчете на год акции А равно 10%, акции В — 15%. Это означает, что акция В рискованнее бумаги А. Учитывая правило трех сигм, инвестор вправе ожидать, что с вероятностью 68,3% через год он может получить по бумаге А доходность в диапазоне от 20% до 40%, а по бумаге В — от 15% до 45%. Поэтому более консервативный вкладчик выберет бумагу А, а более склонный к риску — бумагу В.

Дисперсию как меру риска ввел в теорию портфеля ценных бумаг основоположник современной теории портфеля Г.Марковец. Определенным недостатком данной меры риска является то, что она одинаково учитывает отклонения в доходности актива от его средней доходности как в сторону увеличения, так и снижения. В то же время инвестора, купившего финансовый актив, беспокоит именно снижение его доходности. Рост доходности по сути не является для него риском. Поэтому позже Г.Марковец предложил в качестве меры риска показатель полудисперсии. Выборочная полудисперсия определяется по формуле:

Формула (1.11) отличается от формулы (1.5) только тем что при расчете показателя полудисперсии учитываются только значения доходности актива, которые меньше его ожидаемой доходности. Таким образом, инвесторы получают представление о риске потерь в более прямой форме, чем при расчете дисперсии. В то же время данная мера риска не всегда будет иметь преимущество по сравнению с дисперсией. Так, если доходность актива распределена нормально, то полудисперсия равна половине дисперсии, поскольку нормальное распределение симметрично относительно своего среднего значения. Поэтому использование в этом случае полудисперсии вместо дисперсии не дает инвестору лучшего представления о риске актива. Соответственно безразлично, какую меру риска рассчитывать. В то же время более удобно использовать дисперсию, так как это более простая для расчета и знакомая из математики многим инвесторам величина.

Использование полудисперсии оправдано в отношении активов, доходность которых не характеризуется нормальным распределением, например производных инструментов.

В заключение данного параграфа следует также отметить, что дисперсию актива можно рассчитывать и на основе прогнозов инвестора в отношении конъюнктуры будущего периода. В этом случае инвестор оценивает возможные сценарии ее развития. На этой основе он прогнозирует значения будущих до-ходностей актива и задает им субъективные вероятности. Например, инвестор полагает, что в будущем периоде актив А принесет доходность гх с вероятностью р<, доходность г2 с вероятностью р2 и т.д. доходность гп с вероятностью рп. Сумма всех вероятностей равна 100%. На основе этих данных по формуле (1.1) рассчитывается средняя доходность актива. Далее дисперсия определяется по формуле:

Источник