Byzantine generals problem bitcoin

Byzantine Generals Problem

To help understand the blockchain, let’s examine a classic agreement issue known as The Byzantine Generals problem.

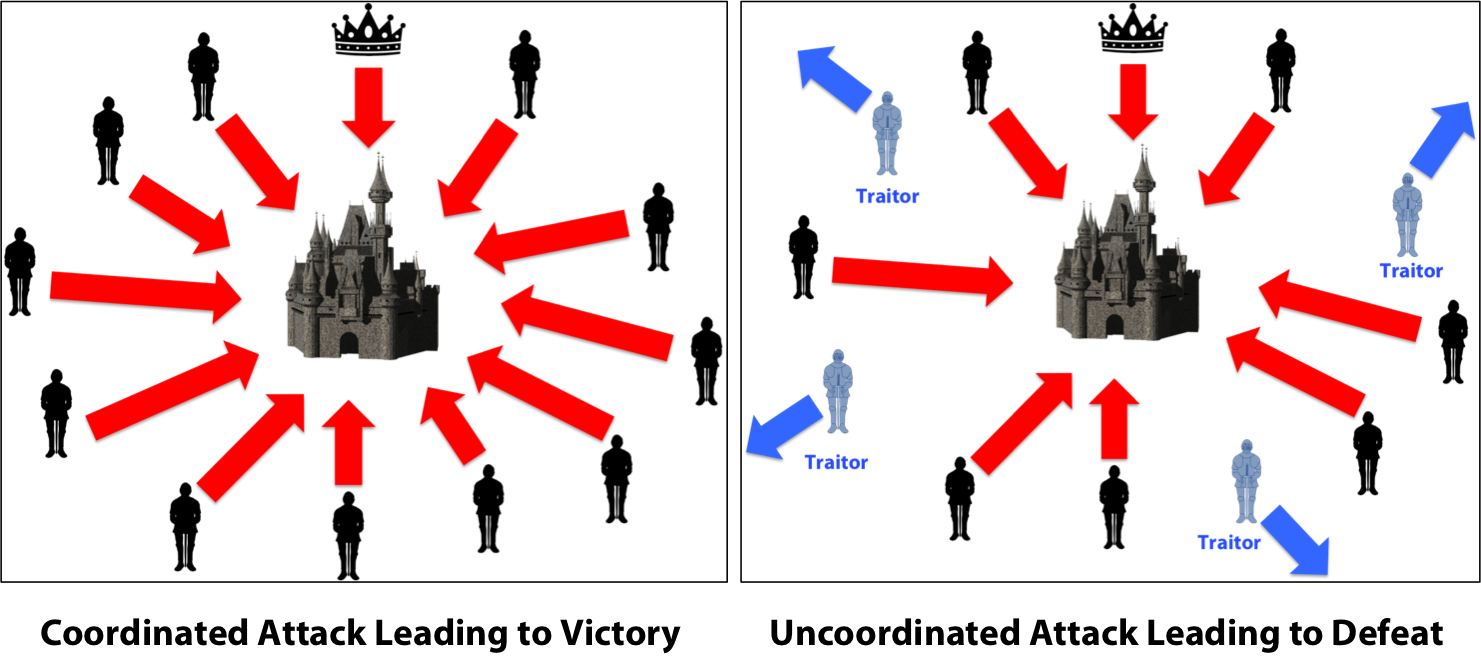
In this scenario, several army troops surround a castle they hope to conquer. Each troop has one general designated as the lead.

The troops are dispersed, so a central command is difficult.

To coordinate, the generals must relay a message instructing when to act, but only a simultaneous attack ensures victory.

The problem is that the generals do not know who is loyal and who is a traitor. So how can the generals reach a collective decision and conquer the castle?

This is where blockchain comes to the rescue.

The blockchain uses a distributed ledger, which functions like the distributed attack. Inputs to the ledger (like the attack messages) must be trusted.

Much like the troops surrounding the castle, how can a network trust the other members AND ensure that the messages are valid?

Here is how:

All participating members must agree on every message that is transmitted. If a member is corrupt -OR- the message is corrupt – then the message will be resisted, and the network will not be affected.

Before broadcasting their message to the block – a miner is required to compute a complex “proof-of-work” puzzle. Solving this correctly creates a hash, validates the message, and a “consensus” is reached.

In the case of the Byzantine generals, proof of work on the blockchain ensures that they can only send trusted messages to the troops, which guarantees a successful coordinated attack.

Источник

Bitcoin’s Proof of Work: The problem of the Byzantine Generals

This article is an excerpt from my book, A brief introduction to Bitcoin.

“It is not sufficient that everyone knows X. We also need everyone to know that everyone knows X, and that everyone knows that everyone knows that everyone knows X — which, as in the Byzantine Generals’ problem, is the classic hard problem of distributed data processing.”

A fundamental problem in distributed networks is finding consensus in the presence of faulty or defective processes. A dependable system must manage the failure of one or more of its components when it either permanently crashes, repeatedly boots-up and shuts-down, or behaves byzantine, meaning damaging in the worst possible way. For example, nodes may deliberately and maliciously misrepresent or contradict information or disseminate information to make it impossible to unify the network. This problem is described in the literature as the “problem of the Byzantine Generals”. It occurs specifically in the case of Bitcoin when the entire network needs to agree on the secure and irreversible validity of transactions, i.e. when it needs to decide which blocks are the generally accepted ones.

The problem of the Byzantine Generals can be described as follows: A number of generals position their armies outside a besieged city they want to conquer, and they need to choose the time of their attack. They know that they can only be victorious if at least half of them attack at the same time. But if they don’t coordinate the time of the attack well, they are outnumbered and will lose the fight. They also suspect that some of the generals are disloyal and will send out fake messages regarding the time of the attack. And since the generals can only communicate with each other via messengers on horseback, they have no way of verifying the authenticity of a message. So we ask ourselves, how can consensus regarding the timing of the attack be reached in these circumstances, despite the lack of trust and without a central governance entity.

Prior to Bitcoin, this problem was considered perhaps impossible to solve. Computer scientists declared in 1982 that the generals’ problem can at most be reduced to a “commander and lieutenant” problem, in which all lieutenants must act in accordance with the commander’s orders, as long as they are loyal. They have shown that the problem can only have a solution if more than two-thirds of the generals are loyal.[1]

Bitcoin seeks to provide a universal solution to the problem, through which the loyalty of more than 50% of the computing capacity is enough to reach consensus. In this case, disagreement is temporarily accepted and the solution to conflicting opinions is determined by majority vote. In other words, consensus is reached because computing resources are scarce and because one’s own performance is used as a vote. This makes it possible to build applications in a decentralised way, which would not have been possible earlier without a central controller. For this reason, the technology behind the Bitcoin protocol — the blockchain and distributed consensus — is increasingly used in other areas too, not only in transaction verification.

Going back to our example, if we regard the generals as an analogy to the individual mining nodes of the Bitcoin network, then the solution offered by Bitcoin looks like this: At any time, any general may announce an attack time. The attack time that is first heard is considered the official plan. However, the transmission of a message is not immediate, which is why different generals can hear different plans first. Therefore, once a general receives a plan, he must solve a difficult mathematical problem based on that plan — a task which preferably lasts multiple minutes on average. As soon as one of them finds a solution, he adds it to the plan, thus generating a new plan. He sends the new plan to the other generals. After that, everyone who hears it begins to expand on this new official plan, which should again take multiple minutes.

Every general is working on the most frequently expanded plan known to him, in order to extend the longest living solution that he has heard until then. After a solution has been expanded multiple times, the attack time contained in the longest chain of calculations (e.g. in the longest plan) is considered to be the true attack time, because it necessarily required more than half of the calculation capacity of all the generals to create it. Put differently, the mere existence of this longest block-chain is proof that the majority of generals (over 50%) were involved in its creation. No attacker with less than half the computing power could have produced another chain of similar length during the same time. This scheme is called “proof-of-work” and the resulting hash-tree structure of the blockchain is shown schematically below.

One aspect of Bitcoin complicates the problem described above. In the problem of the Byzantine Generals a final decision exists with which all nodes agree. For Bitcoin, this requirement does not exist, so no deterministic solution is provided. The Bitcoin protocol is highly probabilistic and random. It guarantees that the decisions will eventually converge, but without setting a final date. This self-stabilising solution adopted by Bitcoin was described by Dijkstra in 1974 and published in 2006 by Angluin and others, and applied to consensus finding in distributed systems. Eventually an agreement on the validity of each block takes place with absolute certainty. At the same time, it cannot be ruled out that at any point in time a longer chain will appear, which supersedes the previous chain. As a result, all transactions in the shorter chain lose their validity from the time the branch out — the so-called “fork” — takes place. Only those transactions remain valid, which have the same inputs and outputs in the long chain as in the short chain. The discrepancy between the two chains may allow, in certain circumstances, the double spending of the same amounts. This is an issue we’ll discuss in the next sub-chapter.

From a technological point of view, such a fork (or branching out) can be expected at certain intervals. A major such fork took place in March 2013. A new version of a Bitcoin software client, due to a lack of backward compatibility, caused older versions of the same client to fail to recognise the generated blocks. This led to old clients working on their own blockchain. The fork existed for 24 blocks — about 6 hours — and disbanded after most of the network switched back to the old version.

Источник

The Byzantine Generals’ Problem steem Created with Sketch.

в #bitcoin • 3 года назад (edited)

Developing a system like Bitcoin that is both distributed and reliable is incredibly difficult. This applies to any form of distributed system however, not just crypto currencies, where there is no central control enforcing trust. This issue has become known as the Byzantine Generals’ Problem (BGP).

Definition

The BGP was first proposed in 1982 relating to computer science fault tolerance and describes it as the following:

«We imagine that several divisions of the Byzantine army are camped outside an enemy city, each division commanded by its own general. The generals can communicate with one another only by messenger. After observing the enemy, they must decide upon a common plan of action. However, some of the generals may be traitors, trying to prevent the loyal generals from reaching agreement. The generals must have an algorithm to guarantee that (A) All loyal generals decide upon the same plan of action and (B) A small number of traitors cannot cause the loyal generals to adopt a bad plan.”

Marshall Pease, Robert Shostak & Leslie Lamport

What does this mean?

Taking a look at the diagram, we can see that traitors can prevent a group from arriving at consensus. Whilst in the Byzantine army, this could be a commander relaying false information, or a rogue lieutenant not passing on messages correctly, within distributed ledger technology this would be a malicious player seeking to process fraudulent transactions.

Send in Satoshi!

Our diagram is a simplistic one, so as you can imagine as a network grows and new users and connections develop, complexity increases exponentially and reaching consensus is far more difficult. This therefore explains why before Bitcoin, decentralised ledgers were not feasible.

The pseudonym Satoshi Nakamoto penned the famous Bitcoin whitepaper on 31st October 2008. It contained arguably the best solution to the BGP developed so far, and now enjoys the broadest adoption.

So how does Bitcoin actually solve this?

The BGP manifests itself within the issue of blockchain synchronisation. How does everyone’s ledger remain in sync and reach consensus in a distributed way? When a transaction is sent across the network, it is broadcast to all users. It is unconfirmed initially however due to the BGP. Users don’t know if a dishonest player has attempted to double spend the same Bitcoin for example, therefore which transaction do they accept? Bitcoin resolves the BGP and is able to confirm transactions through mining.

Mining solves the BGP by ensuring that transactions can only be confirmed if enough computational power was used to solve the block that contained them. This process can be generalised in 3 steps:

Compile Input Data — Miners collate a new block of broadcasted transactions and verify they are valid. The hash of the last blockchain block is added to this along with a random number (called a “nonce”).

Perform a cryptographic calculation (SHA-256 in Bitcoin’s case) to the data from step 1, producing an output hash (a series of characters).

This hash is checked against a desired pattern. If it matches this pattern, the “puzzle” is solved and that miner wins the prize for that block (currently 12.5 BTC, plus the transaction fees from the block). If not, another nonce is tried and the steps are repeated (until someone successfully mines that block and therefore solves the “proof-of-work” problem). The mining difficulty of solving this puzzle is automatically adjusted according to the overall computing power on the network. This way the amount of time it takes to solve a block remains at 10 minutes on average.

The winning block is then verified by nodes and broadcast to the network. In this way it acts like a lottery for who gets to enter the next transactions in the chain, preventing one party from controlling the ledger.

Some may suggest doesn’t this just shift the BGP to the miners however? What if two miners produce blocks at similar times or an attacker is attempting to reverse transactions, how do nodes choose which block to include? In reality it doesn’t shift the problem as nodes must always choose the chain that is the “longest”, therefore the chain that took the most computational power to create. The shorter blockchain is subsequently discarded as an orphan block and its transactions must be processed again if they weren’t already part of the successful block. A traitor cannot statistically act maliciously (such as spending BTC in one block and erasing that transaction in the next) as block creation is random, unless they have enough hash power to produce the majority of new blocks (a 51% attack). The costs and risk of such an attack are so severe in the Bitcoin blockchain that it is highly unlikely. Although mining pools can be made up of many thousands of separate entities working together (for the time being — there is no fixed coalition here) to solve blocks and are therefore unlikely to collude, some have concerns over the combined hashing power of certain pools or related pools. Whenever these percentages have risen too high in the past however, members of these pools have moved voluntarily in order to preserve confidence in the system.

Therefore the process of randomly selecting a nonce to produce a chain, combined with always selecting the longest (most difficult) chain, and provided honest miners have at least 50% of the overall hash power, Bitcoin solves the BGP.

Conclusion

There are certainly caveats, though for the first time in our history, Bitcoin presented a feasible means of creating decentralised ledgers and reaching distributed consensus. As a result it currently enjoys the highest adaption of any such solution. Whilst this may or may not last in the future, it was the zero to one innovation breakthrough in solving the BGP and the implications of this will no doubt extend beyond its initial use case.

By James Hunt (@humanjets)

Источник

Triple-Entry Bookkeeping: How Satoshi Nakamoto Solved the Byzantine Generals’ Problem

In 2008, Satoshi Nakamoto essentially solved the infamous computational issue called the “Byzantine generals’ problem” or the “Byzantine Fault.”

Throughout the history of man, people used ledgers to record economic transactions and property ownership. A ledger is often referred to as the “principal book,” and entries can be recorded in stone, parchment, wood, metal, and with software as well. Ledgers were used for centuries, but the shared ledger system became really popular in 1538 when the church kept records.

In Mesopotamia, which was about 5,000 years ago, scientists discovered Mesopotamians used single-entry accounting ledgers. Much of it was complex and these ledgers accounted for things like property and money. But with a single-entry ledger, all anyone has to do is remove one line of entry or a few lines, and the funds would be gone or disappear from the records.

An old church ledger.

During the Renaissance period, intelligent people discovered double-entry bookkeeping, which literally changed everything in the world of accounting. Our modern financial system is based on the double-entry system created more than six hundred years ago. Double-entry systems grew because trade swelled beyond borders, so people needed a way to maintain records that were far more trustworthy than the single-entry accounting ledgers. Leveraging single-entry accounting would not work well when dealing with people who are thousands of miles away.

The double-entry system was first documented centuries ago by Luca Pacioli (1446–1517), a mathematician and Franciscan friar. Towards the latter part of the 15th century, this system became extremely popular, as it was leveraged by merchants and traders everywhere. Now double-entry bookkeeping isn’t necessarily transparent and these types of books can be private or open. The system does a much better job than single-entry accounting when it comes to errors, fraud detection, and financial reality. But most mathematicians and economists understand that the double-entry system can be manipulated.

So the double-entry system allows an entity to record a total of what is owed and what is owned (Assets = Liabilities + Equity). Alongside this, double-entry accounting keeps a record of what the entity spent and earned. Traditionally this system has two corresponding and equal sides that people call “debit” and “credit.” Historically, people often use the left side for debit entries and the right for credit. One of the biggest issues with the double-entry system is trusting the human and fallible bookkeeper, messenger, or accountant. Moreover, in today’s world of monetary finance, double-entry systems are used regularly, but the world’s central banks are far from transparent or based on financial reality.

**The “Byzantine generals’ problem” or the “Byzantine Fault.” In essence, the Byzantine generals’ problem is an allegory in the field of computer science, which tells a story of two generals (there can be more than two generals) planning to attack an enemy city. The generals tell both armies to attack from each side of the enemy’s castle, the east side and the west side. The issue at hand is a timing or synchronization problem coupled with trust, because both armies need to attack simultaneously. Now the two generals split a group of messengers but the only way the messengers can communicate is by entering via the enemy castle. The Byzantine generals’ problem is not being able to trust the message from the messenger, as it may not be valid or truthful.

When computers came around, ledger systems became far more advanced and people tried to push the double-entry system to the next level. Triple-entry accounting was first conceived in the early eighties and the inventor of the Ricardian contract, Ian Grigg discussed the method well before it was solved. The problem with creating something more advanced than the double-entry accounting system was the notorious “Byzantine generals problem.”

Basically, when a distributed ledger is being shared among computing systems people cannot trust which system or server (node) is trustworthy, compromised, or functioning with a failure to detect. However, on October 31, 2008, an anonymous person(s) released a paper that solved the Byzantine Fault dilemma.

That Halloween, Nakamoto wrote an email to the Cryptography Mailing List which said:

I’ve been working on a new electronic cash system that’s fully peer-to-peer, with no trusted third party — The main properties: Double-spending is prevented with a peer-to-peer network. No mint or other trusted parties. Participants can be anonymous. New coins are made from Hashcash style proof-of-work. The proof-of-work for new coin generation also powers the network to prevent double-spending.

Basically Nakamoto invented the triple-entry accounting system or essentially gave the theory life. Triple-entry bookkeeping is far, far more advanced than the traditional double-entry systems we know of today. Essentially all the accounting entries are cryptographically validated by a third entry by hashing and a nonce.

“Digital signatures provide part of the solution, but the main benefits are lost if a trusted third party is still required to prevent double-spending,” Nakamoto’s infamous white paper says. With the triple-entry bookkeeping system, the entries (transactions) are both congruent, but the infrastructure also adds a third entry into the ledger’s validation process, which again is cryptographically sealed.

Fundamentally, hashing or cryptographic hash function (CHF) is a mathematical function of arbitrary size we call a “message.” A nonce is an arbitrary number that is used one time when the message is concealed in plain text. In the **Byzantine general tale, one army sends a message (CHF) over to the other general with a nonce. The other general then must decipher the CHF, with some partial knowledge cryptographers call a “hash target.” All the general has to do is hash the CHF and the nonce, as well as make sure everything correspond s with the hash target (partial knowledge). If everything is valid, the two generals have easily synchronized the timing of an attack, without having to doubt the message system or messengers.

Satoshi’s white paper also said:

Proof-of-work also solves the problem of determining representation in majority decision making. If the majority were based on one-IP-address-one-vote, it could be subverted by anyone able to allocate many IPs. Proof-of-work is essentially one-CPU-one-vote. The majority decision is represented by the longest chain, which has the greatest proof-of-work effort invested in it. If a majority of CPU power is controlled by honest nodes, the honest chain will grow the fastest and outpace any competing chains.

Nakamoto’s software leverages the Hashcash system, which bolsters the security of the underlying infrastructure by utilizing cryptographic hashes. Hashcash is used for Nakamoto’s proof-of-work (PoW) which is basically a blob of data that is difficult, expensive, and painstaking to produce. However, PoW is also undemanding when it comes to verifying and satisfying the agreement, as long as everyone follows the rules. There are a number of PoW schemes available like Quark, Scrypt, Blake-256, Cryptonight, and HEFTY1, but Nakamoto’s Bitcoin leverages SHA256.

It is “near” impossible or extremely hard to falsify, destroy or edit one or a few lines in the constant SHA256 ledger system. As the proof-of-work continues to build, it becomes extremely expensive and very time consuming to attack. There are other ways that networks can use to come to consensus, like the popular proof-of-stake consensus (PoS) systems. However, PoS has not proven itself as the most reliable system (security-wise) yet in order to come to consensus.

The advantages of triple-entry bookkeeping are huge, and the sky’s the limit when it comes to this relatively new technology. Triple-entry accounting offers a concept that is “near” trustless, if we remove trusting the autonomous system. Auditing, reconciliation, and transparency are all reconsidered notions when it comes to “trusting the books.” Satoshi told people on numerous occasions that he solved the Byzantine generals’ problem. “The proof-of-work chain is a solution to the Byzantine generals’ problem,” Nakamoto told James A. Donald on November 13, 2008.

Bitcoin’s inventor also stressed to Donald a few days earlier that the “proof-of-work chain is the solution to the synchronisation problem, and to knowing what the globally shared view is without having to trust anyone.”

Furthermore, the decentralized currency is pseudo-anonymous, meaning that a person can leverage as much anonymity or transparency as desired. Nakamoto explained the transparency and privacy foundations in the white paper quite well.

“The traditional banking model achieves a level of privacy by limiting access to information to the parties involved and the trusted third party,” the Bitcoin white paper details. “The necessity to announce all transactions publicly precludes this method, but privacy can still be maintained by breaking the flow of information in another place: by keeping public keys anonymous.”

Nakamoto concluded by saying:

The public can see that someone is sending an amount to someone else, but without information linking the transaction to anyone. This is similar to the level of information released by stock exchanges, where the time and size of individual trades, the “tape”, is made public, but without telling who the parties were.

The well known cryptocurrency expert, Andreas M. Antonopoulos does an excellent job explaining the tale of the Byzantine generals’ problem and how it applies to Bitcoin in the video below.

What do you think about Satoshi Nakamoto solving the Byzantine generals’ problem? Let us know what you think about this subject in the comments section below.

Источник