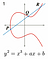Bitcoin get public key from address

How to Generate a Bitcoin Address — Step by Step

Here is a bash script that does what is outlined below: https://bit.ly/2MIgeOD

Introduction

This is a hands-on, technical guide about the generation of Bitcoin addresses including private and public keys, and the cryptography involved.

Learn more and join people in 22 countries around the world in my course on how to Become a Bitcoin + Blockchain Programmer.

This guide will walk you through all the steps to generate a Bitcoin address using the command line on a Mac. Similar steps should be possible on other operating systems using similar cryptographic tools. Lines starting with $ denote terminal commands, which you can type and run (without the $ of course).

Dependencies

• brew — Installation: https://brew.sh/
• pip — Installation: sudo easy_install pip
• libressl — Installation: brew install libressl
• base58 — Installation: pip install base58

Note: To do the contained openssl cli commands, I installed libressl in order for some of the elliptic curve commands to work as the current version of openssl cli on mac has a bug.

Cryptography Primer

Public Key Cryptography

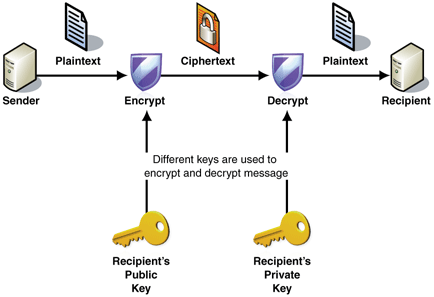
Or asymmetric cryptography, is a type of cryptography that uses key pairs, each of which is unique. The pair of keys includes a public key and a private key. This is the type of cryptography that Bitcoin uses to control funds. A public key can be generated from a private key, but not vice-versa (computationally too difficult). Also, something encrypted with a private key can be decrypted with the public key, and vice-versa, hence they are asymmetric.

• Encryption: When a user has a public key, a message can be encrypted using a public key, which can only be read by the person with the private key. This also works in reverse.
• Digital Signatures: A user can, with their private key and a hash of some data, use a digital signature algorithm such as ECDSA, to calculate a digital signature. Then, another user can use the algorithm to verify that signature using the public key and the hash of the same data. If it passes, this proves a user did in fact submit a specific message, which has not been tampered with.
• Digital Fingerprint: Is a way to represent an arbitrarily large data set by computing the hash of it to generate a fingerprint of a standard size. This fingerprint would be so difficult to replicate without the same exact data, which can be assumed to have not been tampered with.

Private keys are what prove you can send Bitcoin that has been sent to you. It is like the password to your bank account. If you lose it or someone else gets a hold of it, you’re toast.

Public keys help people know how to send you Bitcoin.

Creating a Bitcoin Address

Private Key Generation

Private keys can be any 256 bit (32 byte) value from 0x1 to 0xFFFF FFFF FFFF FFFF FFFF FFFF FFFF FFFF BAAE DCE6 AF48 A03B BFD2 5E8C D036 4140 .¹

The total possible number of private keys is therefore 2²⁵⁶ or 1.16 x 10⁷⁷. Imagine the total number of atoms in your body, then imagine that each of those atoms is an earth. The total number of atoms on all of those earths is about 7 x 10⁷⁷.² There is virtually no chance that your random private key will ever be generated randomly or found by someone else.

A common (but not the most secure) way of creating a private key is to start with a seed, such as a group of words or passphrases picked at random. This seed is then passed through the SHA256 algorithm, which will always conveniently generate a 256 bit value. This is possible because every computer character is represented by an integer value (see ASCII and Unicode).

Note: SHA256 is a one-way, deterministic function meaning that it is easy to compute in one direction, but you cannot reverse it. In order to find a specific output, you have to try all the possible inputs until you get the desired output (brute forcing) and it will always produce the same output given the same input, respectively.

The seed can be used to generate the same private key if the same hashing algorithm is used in the future, so it is only necessary to save the seed.

This private key is in hexadecimal or base 16. Every 2 digits represents 8 bits or 1 byte. So, with 64 characters, there are 256 bits total.

Public Key Generation

Public keys are generated from the private keys in Bitcoin using elliptic curve ( secp256k1 ) multiplication using the formula K = k * G , where K is the public key, k is the private key, and G is a constant called the Generator Point⁴, which for secp256k1 is equal to:

It doesn’t seem to be known how this point was chosen by they designers of the curve. Also, this algorithm is a one-way algorithm, or a “trap door” function so that a private key cannot be derived from the public key. It is important to note that elliptic curve multiplication is not the same as scalar multiplication, though it does share similar properties.

To do this in the terminal from our private key earlier,

This public key contains a prefix 0x04 and the x and y coordinates on the elliptic curve secp256k1 , respectively.

Compressed Public Key

Most wallets and nodes implement compressed public key as a default format because it is half as big as an uncompressed key, saving blockchain space. To convert from an uncompressed public key to a compressed public key, you can omit the y value because the y value can be solved for using the equation of the elliptic curve: y² = x³ + 7. Since the equation solves for y², the right side of the equation could be either positive or negative. So, 0x02 is prepended for positive y values, and 0x03 is prepended for negative ones. If the last binary digit of the y coordinate is 0, then the number is even, which corresponds to positive. If it is 1, then it is negative. The compressed version of the public key becomes:

The prefix is 0x02 because the y coordinate ends in 0xa4 , which is even, therefore positive.

Address Generation

There are multiple Bitcoin address types, currently P2SH or pay-to-script hash is the default for most wallets. P2PKH was the predecessor and stands for Pay to Public Key Hash. Scripts give you more functionality, which is one reason why they are more popular. We’ll first generate a P2PKH original format address, followed by the now standard P2SH .

The public key from the previous output is hashed first using sha256 and then hashed using ripemd160 . This shortens the number of output bytes and ensures that in case there is some unforeseen relationship between elliptic curve and sha256, another unrelated hash function would significantly increase the difficulty of reversing the operation:

Note that since the input is a string, the xxd -r -p will convert the hex string into binary and then output it in hexdump style (ascii), which is what the openssl hashing functions expect as input.

Now that we have hashed the public key, we now perform base58check encoding. Base58check allows the hash to be displayed in a more compact way (using more letters of the alphabet) while avoiding characters that could be confused with each other such as 0 and O where a typo could result in your losing your funds. A checksum is applied to make sure the address was transmitted correctly without any data corruption such as mistyping the address.

Bitcoin P2PKH addresses begin with the version byte value 0x00 denoting the address type and end with a 4 byte checksum. First we prepend the version byte (prefix) to our public key hash and calculate and append the checksum before we encode it using base58 :

Note: -c denotes a checksum is to be applied. The checksum is calculated as checksum = SHA256(SHA256(prefix+data)) and only the first 4 bytes of the hash are appended to the end of the data.

The resulting value is a P2PKH address that can be used to receive Bitcoin: 16JrGhLx5bcBSA34kew9V6Mufa4aXhFe9X

Pay-to-Script Hash

The new default address type is a pay-to-script-hash, where instead of paying to a pubKey hash, it is a script hash. Bitcoin has a scripting language, you can read more about it here. Basically it allows for things like multiple signature requirements to send Bitcoin or a time delay before you are allowed to send funds, etc. A commonly used script is a P2WPKH (Pay to Witness Public Key Hash): OP_0 0x14

where the PubKey Hash is the RIPEMD160 of the SHA256 of the public key, as before, and 0x14 is the number of bytes in the PubKey Hash. So, to turn this script into an address, you simply apply BASE58CHECK to the RIPEMD160 of the SHA256 of the script OP_0 0x14

except you prepend 0x05 to the script hash instead of 0x00 to denote the address type is a P2SH address.

If you like the article, check out my course on how to Become a Bitcoin + Blockchain Programmer.

Источник

How does a wallet get the public key from an address?

I was under the impression that addresses are just an encoded, hashed public keys with a prefix and that only the public key is used on the blockchain (not the address) for transactions. But if the public key is hashed, how does the wallet get the public key from the address to create a transaction?

I did some research which confirmed my doubts that this is not possible. So I was wondering, how does the wallet create a transaction if it doesn’t have the public key?

EDIT: I mean how does someone trying to send 10 BTC get the public key of the receiver for pay to public key from the receivers to address. I fully understand the cryptographic element of private & public keypairs and how bitcoin is spent just not how the public key of the receiver is derived from the address. What I have seen is that (most commonly) transactions are pay to public key hash (P2PKH) rather than what I originally thought which was all txns are pay to public key (P2PK).

4 Answers 4

Simply put, you don’t. The address is a hash of the public key with a checksum and a prefix (1). The reason the addresses are not just public keys is unknown, you would have to ask satoshi that, however it is likely make them shorter. BTC does have P2PK but it is not commonly used as the public key is much longer than an address. Hope this helps!

Perhaps you’re confused by the phrasing «the wallet», as it’s only the receiver’s wallet who needs to know the public key, and he has it, because he created the address in the first place.

In what follows, I’m going to assume a standard 1. address (pay to pubkey hash). That’s not the only type of address, but similar ressonings apply to every type of addresses.

In the normal workflow, there are two wallets involved. Let’s call them Suzy (the sender) and Rudy (the receiver).

• Rudy generates a private key x.
• Rudy computes the public key corresonding to x, called P.
• Rudy computes the addreds A corresponding to P by hashing it.
• Rudy sends A to Suzy (by sending it in person, or putting it on a website, or showing it as a QR code, or . ).
• Suzy constructs a transaction that contains an output addressed to A. Suzy has no clue what public key A corresponds to, but also doesn’t care. This address really encodes «require a public key and a signature valid for that key, and the hash of the public key needs to be A».
• Suzy broadcasts the transaction on the network, where it will be picked up by miners who put it in a block, finalizing the transfer.
• Now when Rudy wants to spend the coins he received from Suzy, he needs to satisfy the condition that Suzy put in the transaction. This requires the public key P (as that’s the only known public key whose hash is A), and a signature created using private key x (which is the only private key that can construct signatures that are valid for P). Thankfully, Rudy has both x and P, because he was the one who created them.

Источник

Blockchain на Go. Часть 5: Адреса

Вступление

В предыдущей статье мы начали реализацию транзакций, а также ознакомились с принципом ее работы: нет учетных записей, личные данные (например, имя или серия и номер паспорта) не требуются и не хранятся нигде в Bitcoin. Но все же должно быть что-то, что идентифицирует вас как владельца выходов транзакции (т. е. владельца монет, заблокированных на выходах). И это то, для чего нужны адреса в Bitcoin. До сих пор мы использовали произвольные строки в качестве адресов, теперь пришло время реализовать реальные адреса, таким образом, каким они реализованы в Bitcoin.

В этой части мы изменим очень много кода, поэтому я не вижу смысла объяснять все подробно. Посетите эту страницу, чтобы увидеть все изменения, по сравнению с прошлой статьей.

Биткоин-адрес

Вот пример Bitcoin-адреса: 1A1zP1eP5QGefi2DMPTfTL5SLmv7DivfNa. Это самый первый Bitcoin-адрес, который якобы принадлежит Сатоши Накамото. Bitcoin-адреса находятся в открытом доступе. Если вы захотите отправить кому-то монеты, вам нужно знать адрес получателя. Но адреса (несмотря на уникальность) не являются идентификатором вас, как владельца «кошелька». Фактически, такие адреса являются открытым ключом. В Bitcoin ваша личность — это пара (или пары) закрытых и открытых ключей, хранящихся на вашем компьютере (или в каком-либо другом месте, к которому у вас есть доступ). Для создания таких ключей используются криптографические алгоритмы, которые гарантируют, что никто другой не сможет получить доступ к вашим монетам без физического доступа к вашим ключам. Давайте рассмотрим, что же это за алгоритмы.

Криптосистема с открытым ключом

Алгоритмы криптосистем с открытым ключом используют пары ключей: открытые и закрытые. Открытые ключи можно сообщить кому угодно. Закрытые ключи, напротив, не должны раскрываться никому: никто, кроме владельца, не должен иметь к ним доступа, поскольку это личные ключи, которые служат идентификатором владельца. Ваше лицо — это ваши закрытые ключи (в мире криптовалюты, конечно).

По сути, Bitcoin-кошелек — это всего лишь пара таких ключей. Когда вы устанавливаете приложение кошелька или используете Bitcoin клиент для создания нового адреса, для вас генерируется пара ключей. Тот, кто контролирует закрытый ключ, контролирует все монеты, которые были на него отправлены.

Закрытые и открытые ключи — это просто случайные последовательности байтов, поэтому они не могут быть напечатаны на экране и прочитаны человеком. Вот почему Bitcoin использует алгоритм для преобразования открытых ключей в удобочитаемую строку.

Если вы когда-нибудь использовали Bitcoin кошелек в виде приложения, вероятно, для вас была создана мнемоническая фраза. Такие фразы используются вместо закрытых ключей и могут быть использованы для их генерации. Этот механизм реализован в BIP-039.

Итак, теперь мы знаем, что идентифицирует пользователей в Bitcoin. Но как Bitcoin проверяет владельца выхода транзакции (и монеты, которые там хранятся)?

Электронная цифровая подпись

В математике и криптографии существует концепция электронной цифровой подписи — алгоритмы, которые гарантируют:

1. что данные не были изменены при передаче от отправителя к получателю;
2. что данные были созданы определенным отправителем;
3. что отправитель не может отрицать то, что именно он отправил эти данные.

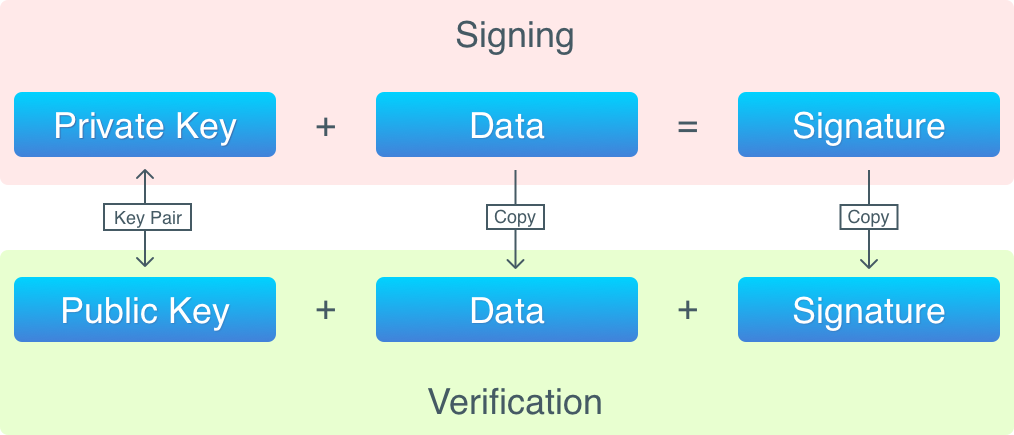
Применяя алгоритм электронной цифровой подписи к данным (т. е. подписывая данные), получается подпись, которую впоследствии можно будет проверить. Подпись данных происходит с использованием закрытого ключа, а для проверки требуется открытый ключ.

Чтобы подписать данные, нам понадобится следующее:

1. данные для подписи;
2. закрытый ключ.

Алгоритм создает подпись, которая хранится во входах транзакции. Чтобы проверить подпись, необходимо следующее:

1. данные, которые были подписаны;
2. подпись;
3. открытый ключ.

Говоря простыми словами, процесс проверки может быть описан так: нам надо убедиться, что подпись получена из этих данных с помощью закрытого ключа, который использовался для генерации открытого ключа.

Цифровые подписи не шифруются, а данные получить из нее невозможно. Это похоже на хеширование: вы преобразуете данные при помощи алгоритма и получаете их уникальное представление. Разница между хешем и подписью — это пары ключей, которые позволяют произвести проверку последней.
Но такие пары ключей также можно использовать и для шифрования данных: для шифрования используется закрытый ключ, а для расшифровки — открытый. Однако же Bitcoin не использует алгоритмы шифрования.

Каждый вход транзакции в Bitcoin подписывается тем, кто создал эту транзакцию. Каждая транзакция в Bitcoin должна быть проверена перед тем, как поместить ее в блок. Верификация означает (помимо других процедур):

1. Проверку того, что входы имеют достаточные права на использование выходов из предыдущих транзакций.
2. Проверку правильности подписи транзакции.

Схематически, процесс подписи и проверки данных выглядит так:

Давайте рассмотрим полный жизненный цикл транзакции:

1. В самом начале содержится блок генезиса с coinbase транзакцией. В транзакциях coinbase нет реальных входов, поэтому подпись не требуется. Вывод транзакции содержит хешированный открытый ключ (используются алгоритмы RIPEMD16(SHA256(PubKey)) ).
2. Когда кто-то отправляет монеты, создается транзакция. Входы транзакции будут ссылаться на выходы из предыдущих транзакций. Каждый вход будет хранить открытый ключ (не хешированный) и подпись всей транзакции.
3. Другие узлы в сети Bitcoin, которые получат транзакцию, тоже проверят ее. Помимо прочего, здесь происходит сопоставление хеша открытого ключа на входе транзакции с хешом соответствующего выхода, (это гарантирует, что отправитель тратит только принадлежащие ему монеты); подпись правильная (это гарантирует, что транзакция создана реальным владельцем монет).
4. Когда узел готов к майнингу нового блока, он поместит транзакцию в блок и начнет добывать ее.
5. Когда блок добыт, каждый другой узел в сети получает сообщение о том, что блок добыли и добавляет его в цепь.
6. После того, как блок добавлен в цепь, транзакция завершена, теперь на ее выходы можно ссылаться в новых транзакциях.

Эллиптическая криптография

Как мы уже с вами говорили, открытые и закрытые ключи представляют собой последовательности случайных байтов. Мы не хотим генерировать закрытый ключ, принадлежащий кому-то другому, поэтому возникает необходимость в особом алгоритме для генерации последовательностей.

Bitcoin использует эллиптические кривые для генерации секретных ключей. Эллиптические кривые — это сложная математическая концепция, которую мы не будем здесь подробно объяснять (если интересно, можете почитать об этом здесь ПРЕДУПРЕЖДЕНИЕ: очень много математики!). Кривая, используемая Bitcoin, может случайным образом выбирать число между 0 и 2²⁵⁶ (что составляет приблизительно 10⁷⁷, на заметку, атомов в видимой вселенной где-то между 10⁷⁸ и 10⁸²). Такой предел означает, что почти невозможно сгенерировать один и тот же закрытый ключ дважды.

Кроме того, Bitcoin использует (и мы будем) алгоритм ECDSA для подписи транзакций.

Base58

Теперь давайте вернемся к вышеупомянутому адресу 1A1zP1eP5QGefi2DMPTfTL5SLmv7DivfNa. Теперь мы знаем, что это общепринятое для человека представление открытого ключа. И если мы его декодируем, он будет выглядеть примерно так (как последовательность байтов, записанных в шестнадцатеричной системе):

Bitcoin использует алгоритм Base58 для преобразования открытых ключей в читаемый человеком формат. Алгоритм очень похож на известный Base64, но он использует более короткий алфавит: некоторые буквы были удалены из алфавита, чтобы избежать гомографические атаки. В связи с этим, в этом алфавите отсутствуют следующие символы: 0 (ноль), О (заглавная буква «о»), I (заглавная «i»), l (строчная «L») а также знаки «+» и «/».

Примерно так выглядит процесс получения адреса из открытого ключа:

Следуя этой схеме, ключ, который мы привели выше, разделен на три части:

Хорошо, теперь, когда мы собрали все воедино, пришло время писать код! Я надеюсь, что сейчас все, что было непонятным прояснится.

Реализация адресов

Начнем со структуры кошелька Wallet

Кошелек — не что иное, как пара ключей. Нам также понадобится тип Wallets , чтобы хранить коллекцию кошельков, сохранять их в файл и выгружать их из него. В конструкторе Wallet создается новая пара ключей. Функция newKeyPair проста, здесь мы используем ECDSA. Затем создается закрытый ключ с использованием кривой, и открытый ключ генерируется при помощи закрытого ключа. Одно замечание: в алгоритмах на основе эллиптической кривой открытые ключи являются точками на кривой. Таким образом, открытый ключ представляет собой комбинацию координат X, Y. В Bitcoin эти координаты объединяются и образуют открытый ключ.

Теперь, создадим функцию генерации адреса:

Разберем по шагам преобразование открытого ключа в адрес Base58:

1. Возьмем открытый ключ и запишем его дважды с помощью алгоритмов хеширования RIPEMD160 (SHA256 (PubKey)) .
2. Подготовим версию.
3. Вычислим контрольную сумму путем хеширования результата из шага 2 и SHA256 (SHA256 (payload)) . Контрольная сумма — это первые четыре байта полученного хеша.
4. Добавим контрольную сумму в комбинацию version+PubKeyHash .
5. Зашифруем комбинацию version+PubKeyHash+checksum при помощи Base58.

В результате вы получите настоящий адрес Bitcoin, вы можете даже проверить его баланс на blockchain.info. Но я больше чем уверен, что на счету этого адреса ничего не будет. Вот почему выбор правильного алгоритма шифрования с открытым ключом настолько важен: учитывая, что закрытые ключи являются случайными числами, вероятность генерации одного и того же числа должна быть как можно меньше. В идеале он не должен повторятся вообще.

Обратите внимание, что вам не нужно подключаться к узлу Bitcoin для получения адреса. Алгоритм генерации адресов использует комбинацию алгоритмов, которые уже реализованы во многих стандартных библиотеках популярных языков программирования.

Теперь нам нужно изменить входы и выходы для использования адресов:

Обратите внимание, что мы больше не используем поля ScriptPubKey и ScriptSig , вместо этого ScriptSig разделяется на поля Signature и PubKey , а ScriptPubKey переименован в PubKeyHash . Мы будем реализовывать те же функции блокировки/разблокировки выходов и логику подписей входов, как в Bitcoin, но реализуем мы это при помощи методов.

Метод UsesKey проверяет, что вход использует определенный ключ для разблокировки выхода. Обратите внимание, что входы хранят нехешированные открытые ключи, а функция принимает хешированный. IsLockedWithKey проверяет, был ли использован хеш-ключ открытого ключа для блокировки выхода. Это дополнительная функция для UsesKey , и они обе используются в FindUnspentTransactions для построения соединений между транзакциями.

Lock просто блокирует выход. Когда мы отправляем монеты кому-то, нам известен только адрес, поэтому функция принимает адрес как единственный аргумент. Затем адрес декодируется, а хеш-ключ открытого ключа извлекается из него и сохраняется в поле PubKeyHash .

Теперь давайте проверим, что все работает правильно:

Отлично! Пришла пора реализовать подписи транзакций.

Реализация подписей

Транзакции необходимо подписывать, так как это единственный способ гарантии в Bitcoin надежности транзакций. Если подпись недействительна, транзакция считается недействительной и, следовательно, не может быть добавлена в цепочку.

У нас есть все для реализации подписей к транзакциям, кроме одного: данных для подписи. Какую часть транзакции мы должны подписывать? Или же необходимо подписывать сделку в целом? Выбор данных для подписи очень важен. Дело в том, что данные, которые должны быть подписаны, должны содержать информацию, которая идентифицирует данные уникальным образом. Например, нет смысла подписывать только выходные значения, потому что такая подпись не будет учитывать отправителя и получателя.

Учитывая, что транзакции разблокируют предыдущие выходы, перераспределяют их значения и блокируют новые выходы, должны быть подписаны следующие данные:

1. Хеши открытых ключей хранящиеся в разблокированных выходах. Это идентифицирует «отправителя» транзакции.
2. Хеши открытых ключей хранящиеся в новых, заблокированных, выходах. Это идентифицирует «получателя» транзакции.
3. Значения новых выходов.

В Bitcoin логика блокировки/разблокировки хранится в скриптах, которые хранятся в ScriptSig и ScriptPubKey полей входов и выходов соответственно. Поскольку Bitcoin допускает разные типы таких скриптов, он подписывает все содержимое ScriptPubKey .

В связи с этим в Bitcoin происходит подпись не транзакции, а ее обработанной копии со входами, содержащими ScriptPubKey указанного выхода

Здесь описан подробный процесс обработки копии транзакции. Скорее всего, он устарел, но мне не удалось найти более надежный источник информации.

Все это выглядит достаточно сложным, давайте начнем писать код. А начнем мы с метода Sign :

Метод принимает закрытый ключ и ассоциативный массив предыдущих транзакций. Как уже упоминалось выше, для подписания транзакции нам необходимо получить доступ к выходам, указанным во входах транзакции, поэтому нам нужны транзакции, которые хранят эти выходы.

Давайте внимательнее рассмотрим этот метод:

Coinbase транзакции не подписаны, так как в них нет реальных выходов

Мы подписываем обработанную копию, а не всю транзакцию:

Копия будет включать все входы и выходы, а TXInput.Signature и TXInput.PubKey будут равны nil.

Затем пройдемся по каждому входу в копии:

На каждом входе Signature устанавливается на nil (просто двойная проверка), а PubKey присваиваем ссылку на выход в PubKeyHash . В настоящий момент все транзакции, кроме текущей, являются «пустыми», то есть поля подписи и PubKey равны нулю. Таким образом, входы подписываются отдельно, хотя это необязательно для нашего приложения, но Bitcoin позволяет транзакциям содержать входы, ссылающиеся на различные адреса.

Метод Hash сериализует транзакцию и хеширует ее с помощью алгоритма SHA-256. Результатом являются данные готовые для подписи. После получения хеша мы должны сбросить поле PubKey , чтобы не было влияния на наши дальнейшие итерации.

Мы подписываем txCopy.ID при помощи privKey . Подпись ECDSA представляет собой пару чисел, которые мы объединяем и сохраняем в поле входа Signature .

Рассмотрим функцию верификации:

Метод довольно простой. Для начала получим копию транзакции, как в прошлом методе:

Затем нам понадобится кривая, которая используется для генерации пар ключей:

Затем пройдемся по всем входам и проверим, что они подписаны:

Эта часть идентична той, что используется в методе Sign, так как во время проверки нам нужны те же самые данные, что мы и подписывали

Здесь мы распаковываем значения, хранящиеся в TXInput.Signature и TXInput.PubKey , так как сигнатура представляет собой пару чисел, а открытый ключ — это пара координат. Мы конкатенировали их раньше для хранения, и теперь нам нужно их распаковать для использования в функциях crypto/ecdsa .

Теперь мы создаем ecdsa.PublicKey , используя открытый ключ, который мы берем из входа, и выполняем ecdsa.Verify , передавая подпись, из входа. Если все входы проверены, мы возвращаем true; если хотя бы один вход не прошел проверку, возвращаем false.

Теперь нам нужна функция для получения предыдущих транзакций. Поскольку для этого требуется взаимодействие со всей цепью, мы сделаем его методом Blockchain :

FindTransaction находит транзакцию по идентификатору (для этого требуется итерация по всем блокам в цепи); SignTransaction берет одну транзакцию, находит транзакции, на которые она ссылается, и подписывает ее; VerifyTransaction просто проверяет транзакцию.

Теперь нам нужно подписать и проверить транзакции. Подписывать мы будем в методе NewUTXOTransaction :

Проверка транзакции происходит до того, как она будет добавлена в блок:

Вот и все! Давайте проверим все еще раз:

У нас даже ничего не сломалось, удивительно!

Давайте закомментируем вызов bc.SignTransaction (& tx, wallet.PrivateKey) в NewUTXOTransaction , для гарантии того, что неподписанные транзакции нельзя будет майнить:

Заключение

Мы реализовали почти все ключевые особенности Bitcoin и это потрясающе. А в следующей части мы наконец-таки завершим реализацию транзакций.

Источник