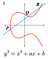Bitcoin compressed public key

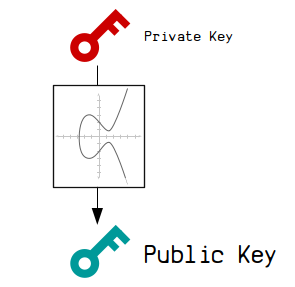
Public Key

A unique number mathematically generated from a private key.

A public key is like an account number that you use to receive bitcoins.

It is created from your private key , which is like a password for that account number.

Try it! — Generate Public Key

How do you generate a public key?

You use your private key (which is just a big random number) to generate a corresponding public key.

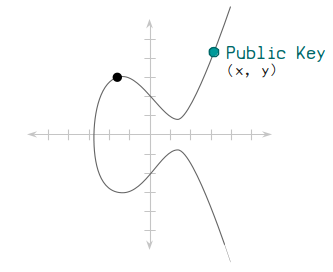
You perform elliptic curve multiplication using your private key, which will give you a final resting point on the elliptic curve. The x and y coordinate of this point is your public key .

Here’s some basic code for creating a public key from a private key .

I haven’t explained how the elliptic curve mathematics works, but I’ve included this code anyway to show how you can get started with calculating a public key for yourself.

Why is the elliptic curve used?

The use of elliptical curve multiplication gives you a mathematical connection from your private key to your public key. It also has two important properties:

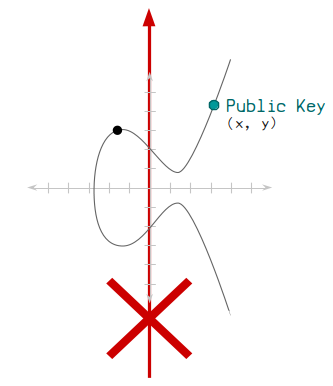
1. It’s not known how to work backwards to get the private key.

You can go forwards using elliptic curve multiplication, but you cannot do mathematics to go backwards.

This means that there is a mathematical connection going from your private key to your public key, but nobody can use your public key to figure out what your private key is.

Therefore you can give out your public key, but also keep your private key a secret.

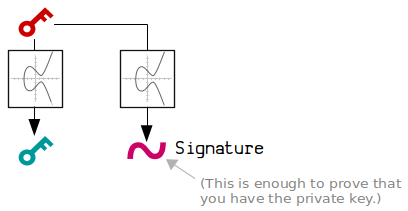
2. You can prove that you have the private key without giving it away.

Basically, using some more elliptic curve mathematics, you can create a digital signature that proves that you have the corresponding private key for a public key, without ever having to give away your actual private key.

It’s like saying you have the password to an account, but you don’t have to show anyone your actual password to prove it.

This is thanks to the seeming magic of digital signatures, and it’s all made possible through elliptic curve mathematics.

Public Key Format

A public key is just the x and y co-ordinate of a point on the elliptic curve. It’s usually stored in hexadecimal format.

There are two formats for public keys:

1. Uncompressed

This is the old format. It has generally stopped being used in favor of the shorter compressed format.

Bitcoin originally used both the x and y coordinate to store the public key.

In this uncompressed format, you just place the x and y coordinate next to each other, then prefix the whole thing with an 04 to show that it is an uncompressed public key:

Here’s an example of what an uncompressed public key looks like:

2. Compressed

However, because the elliptic curve is symmetrical along its x-axis, each x coordinate will only ever have one of two possible y coordinates.

And here’s the trick…

• If y is even, it corresponds to one of the points.
• If y is odd, it corresponds to the other.

So in the compressed public key format, we just store the full x coordinate, along with a prefix that indicates whether the y is even or odd.

We only need to store whether the y coordinate is even or odd.

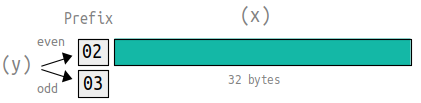
Here’s an example of what a compressed public key looks like compared to an uncompressed public key:

This compressed format ultimately allows us to work out the full x and y coordinates, but saves a lot of space inside the blockchain (i.e. when we create transactions that lock outputs to specific public keys).

How to decompress a public key

You can decompress a compressed public key by solving the curve equation y^2 = x^3 + 7 .

This will give you the missing possible y values for the uncompressed key. You can then use the prefix from the compressed key to determine which y value to use (because the square root of any number has two possible answers, e.g. 16 = +4 or -4 ).

How are public keys used in Bitcoin?

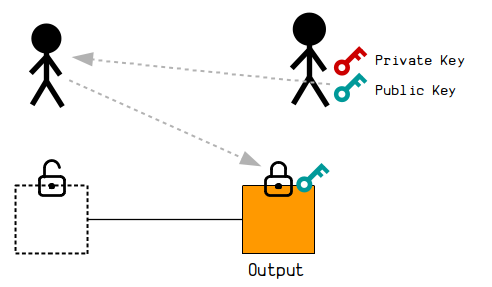
You can give your public key away to people so that they can include it in the the locking script of an output when they create a transaction.

We can give people our public key so that they can send us bitcoins. This is called Pay-To-Pubkey (P2PK)

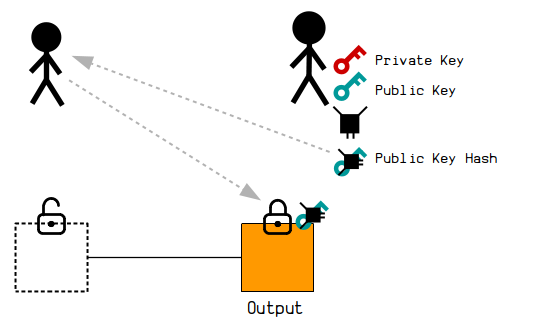
However, in Bitcoin we now more commonly hash160 our public key before giving it away. The public key is then used only when we come to unlocking the output. (The initial lock will then want to check that the public key hashes correctly first before going on to check it against the signature.)

The Hash160 of our public key now sits in the lock. This is called Pay-To-PubKey-Hash (P2PKH)

Where can you find public keys inside the blockchain?

If your looking through raw blockchain data, public keys can typically be found inside transaction data.

1. The public key hash sits within the locking code (scriptPubKey) of an output.

Then in the next transaction that spends the bitcoins…

1. The original public key can then be found inside the unlocking code (scriptSig) of the input.

As you can see, the 04 at the start of the public key indicates that it’s an uncompressed public key. This makes it almost twice as long as the compressed public keys typically used today.

Libraries

In most languages today you can use an existing elliptic curve library to help you create public keys (instead of having to code the mathematics yourself). For example:

• Ruby: github.com/DavidEGrayson/ruby_ecdsa
• PHP: github.com/BitcoinPHP/BitcoinECDSA.php

Resources

By Greg Walker, 10 March 2018

Last Updated: 12 Apr 2021

• 12 Apr 2021: removed trailing full stop from heading
• 10 Apr 2021: updated example compressed and uncompressed public keys
• 29 Mar 2021: /technical/ecdsa — first draft
• 09 Mar 2021: added ecc_multiply.rb code for calculating a public key from a private key
• 19 Oct 2020: Added code example for decompressing a public key.
• 08 Oct 2020: p2pkh link
• 21 Jul 2020: renamed /guide/ to /technical/

I’ll let you know about cool website updates, or if something seriously interesting happens in bitcoin.

Источник

How to Generate a Bitcoin Address — Step by Step

Here is a bash script that does what is outlined below: https://bit.ly/2MIgeOD

Introduction

This is a hands-on, technical guide about the generation of Bitcoin addresses including private and public keys, and the cryptography involved.

Learn more and join people in 22 countries around the world in my course on how to Become a Bitcoin + Blockchain Programmer.

This guide will walk you through all the steps to generate a Bitcoin address using the command line on a Mac. Similar steps should be possible on other operating systems using similar cryptographic tools. Lines starting with $ denote terminal commands, which you can type and run (without the $ of course).

Dependencies

• brew — Installation: https://brew.sh/
• pip — Installation: sudo easy_install pip
• libressl — Installation: brew install libressl
• base58 — Installation: pip install base58

Note: To do the contained openssl cli commands, I installed libressl in order for some of the elliptic curve commands to work as the current version of openssl cli on mac has a bug.

Cryptography Primer

Public Key Cryptography

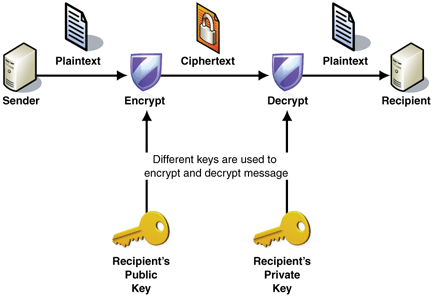
Or asymmetric cryptography, is a type of cryptography that uses key pairs, each of which is unique. The pair of keys includes a public key and a private key. This is the type of cryptography that Bitcoin uses to control funds. A public key can be generated from a private key, but not vice-versa (computationally too difficult). Also, something encrypted with a private key can be decrypted with the public key, and vice-versa, hence they are asymmetric.

• Encryption: When a user has a public key, a message can be encrypted using a public key, which can only be read by the person with the private key. This also works in reverse.
• Digital Signatures: A user can, with their private key and a hash of some data, use a digital signature algorithm such as ECDSA, to calculate a digital signature. Then, another user can use the algorithm to verify that signature using the public key and the hash of the same data. If it passes, this proves a user did in fact submit a specific message, which has not been tampered with.
• Digital Fingerprint: Is a way to represent an arbitrarily large data set by computing the hash of it to generate a fingerprint of a standard size. This fingerprint would be so difficult to replicate without the same exact data, which can be assumed to have not been tampered with.

Private keys are what prove you can send Bitcoin that has been sent to you. It is like the password to your bank account. If you lose it or someone else gets a hold of it, you’re toast.

Public keys help people know how to send you Bitcoin.

Creating a Bitcoin Address

Private Key Generation

Private keys can be any 256 bit (32 byte) value from 0x1 to 0xFFFF FFFF FFFF FFFF FFFF FFFF FFFF FFFF BAAE DCE6 AF48 A03B BFD2 5E8C D036 4140 .¹

The total possible number of private keys is therefore 2²⁵⁶ or 1.16 x 10⁷⁷. Imagine the total number of atoms in your body, then imagine that each of those atoms is an earth. The total number of atoms on all of those earths is about 7 x 10⁷⁷.² There is virtually no chance that your random private key will ever be generated randomly or found by someone else.

A common (but not the most secure) way of creating a private key is to start with a seed, such as a group of words or passphrases picked at random. This seed is then passed through the SHA256 algorithm, which will always conveniently generate a 256 bit value. This is possible because every computer character is represented by an integer value (see ASCII and Unicode).

Note: SHA256 is a one-way, deterministic function meaning that it is easy to compute in one direction, but you cannot reverse it. In order to find a specific output, you have to try all the possible inputs until you get the desired output (brute forcing) and it will always produce the same output given the same input, respectively.

The seed can be used to generate the same private key if the same hashing algorithm is used in the future, so it is only necessary to save the seed.

This private key is in hexadecimal or base 16. Every 2 digits represents 8 bits or 1 byte. So, with 64 characters, there are 256 bits total.

Public Key Generation

Public keys are generated from the private keys in Bitcoin using elliptic curve ( secp256k1 ) multiplication using the formula K = k * G , where K is the public key, k is the private key, and G is a constant called the Generator Point⁴, which for secp256k1 is equal to:

It doesn’t seem to be known how this point was chosen by they designers of the curve. Also, this algorithm is a one-way algorithm, or a “trap door” function so that a private key cannot be derived from the public key. It is important to note that elliptic curve multiplication is not the same as scalar multiplication, though it does share similar properties.

To do this in the terminal from our private key earlier,

This public key contains a prefix 0x04 and the x and y coordinates on the elliptic curve secp256k1 , respectively.

Compressed Public Key

Most wallets and nodes implement compressed public key as a default format because it is half as big as an uncompressed key, saving blockchain space. To convert from an uncompressed public key to a compressed public key, you can omit the y value because the y value can be solved for using the equation of the elliptic curve: y² = x³ + 7. Since the equation solves for y², the right side of the equation could be either positive or negative. So, 0x02 is prepended for positive y values, and 0x03 is prepended for negative ones. If the last binary digit of the y coordinate is 0, then the number is even, which corresponds to positive. If it is 1, then it is negative. The compressed version of the public key becomes:

The prefix is 0x02 because the y coordinate ends in 0xa4 , which is even, therefore positive.

Address Generation

There are multiple Bitcoin address types, currently P2SH or pay-to-script hash is the default for most wallets. P2PKH was the predecessor and stands for Pay to Public Key Hash. Scripts give you more functionality, which is one reason why they are more popular. We’ll first generate a P2PKH original format address, followed by the now standard P2SH .

The public key from the previous output is hashed first using sha256 and then hashed using ripemd160 . This shortens the number of output bytes and ensures that in case there is some unforeseen relationship between elliptic curve and sha256, another unrelated hash function would significantly increase the difficulty of reversing the operation:

Note that since the input is a string, the xxd -r -p will convert the hex string into binary and then output it in hexdump style (ascii), which is what the openssl hashing functions expect as input.

Now that we have hashed the public key, we now perform base58check encoding. Base58check allows the hash to be displayed in a more compact way (using more letters of the alphabet) while avoiding characters that could be confused with each other such as 0 and O where a typo could result in your losing your funds. A checksum is applied to make sure the address was transmitted correctly without any data corruption such as mistyping the address.

Bitcoin P2PKH addresses begin with the version byte value 0x00 denoting the address type and end with a 4 byte checksum. First we prepend the version byte (prefix) to our public key hash and calculate and append the checksum before we encode it using base58 :

Note: -c denotes a checksum is to be applied. The checksum is calculated as checksum = SHA256(SHA256(prefix+data)) and only the first 4 bytes of the hash are appended to the end of the data.

The resulting value is a P2PKH address that can be used to receive Bitcoin: 16JrGhLx5bcBSA34kew9V6Mufa4aXhFe9X

Pay-to-Script Hash

The new default address type is a pay-to-script-hash, where instead of paying to a pubKey hash, it is a script hash. Bitcoin has a scripting language, you can read more about it here. Basically it allows for things like multiple signature requirements to send Bitcoin or a time delay before you are allowed to send funds, etc. A commonly used script is a P2WPKH (Pay to Witness Public Key Hash): OP_0 0x14

where the PubKey Hash is the RIPEMD160 of the SHA256 of the public key, as before, and 0x14 is the number of bytes in the PubKey Hash. So, to turn this script into an address, you simply apply BASE58CHECK to the RIPEMD160 of the SHA256 of the script OP_0 0x14

except you prepend 0x05 to the script hash instead of 0x00 to denote the address type is a P2SH address.

If you like the article, check out my course on how to Become a Bitcoin + Blockchain Programmer.

Источник