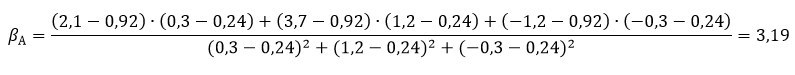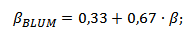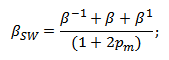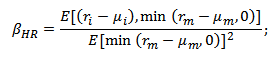Бета коэффициент это доходность

Бета коэффициент

Риски: без их расчета на фондовом рынке никуда. В предыдущих статьях мы разбирали стандартное отклонение и дисперсию (в статье волатильность), как меру риска, сегодня поговорим о коэффициенте бета.

СОДЕРЖАНИЕ СТАТЬИ:

Коэффициент бета β – показатель ценной бумаги (портфеля), который рассчитывается как мера рыночного риска и дает оценку относительного изменения доходности ценной бумаги (портфеля) по сравнению с доходностью рынка в целом. Проще говоря, этот коэффициент показывает, как рынок воздействует на ценную бумагу.

Коэффициент бета необходим для:

— определения рыночного риска актива (портфеля) относительно рынка в целом;

— составление портфеля, нейтрального к риску;

— расчета оценки стоимости капитала.

Формула беты и ее возможные значения

Общепринятый подход к оценке параметра «бета акции» основывается на регрессионном анализе доходности акции относительно доходности фондового индекса.

Классическая бета или, как ее еще называют «сырая», необработанная бета (raw beta):

β – коэффициент бета;

cov (r, p) – ковариация ценной бумаги и портфеля (вместо портфеля часто применяют рыночный индекс, например, индекс Московской Биржи и индекс РТС);

r – доходность актива (ценной бумаги);

p – доходность портфеля (фондового индекса);

σ_p 2 – дисперсия портфеля (фондового индекса).

Значения, которые может принимать бета:

β = 1 – доходность такой бумаги будет изменяться одинаково с доходностью рынка (фондового индекса);

β > 1 – доходность (а также изменчивость) таких бумаг очень чувствительна к изменению рынка. Такие активы больше подвержены риску, но потенциально более доходны. В целом, такие ценные бумаги можно назвать агрессивными;

β – коэффициент бета;

r_i – доходность актива в i-ый момент времени;

p_i – доходность портфеля (индекса) в i-ый момент времени;

r _ср – доходность актива в i-ый момент времени;

р _ср – доходность портфеля (индекса) в i-ый момент времени;

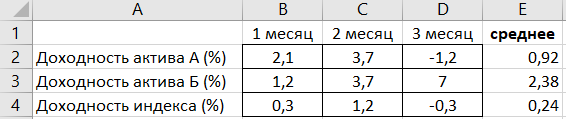
Пример для расчета беты

Совершим расчет беты для актива А

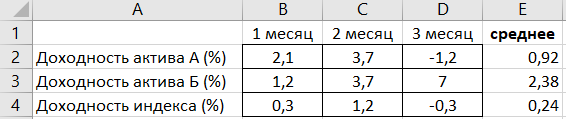
Тот же пример, но с расчетом в Excel

— с помощью опции вставить функцию :

А именно, =ИНДЕКС(ЛИНЕЙН(B2:D2;B4:D4);1) = 3,14

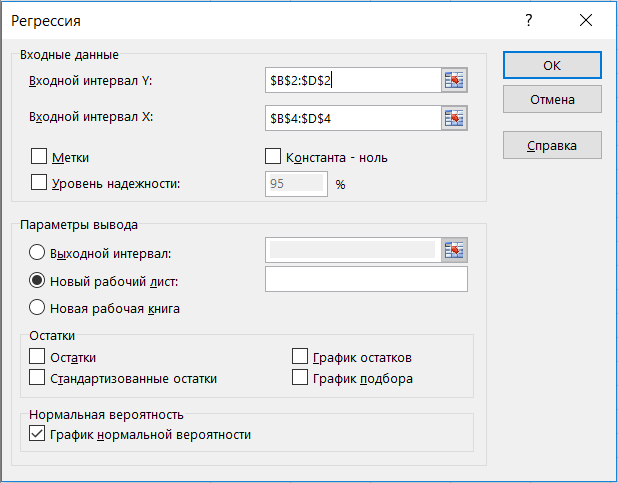
— с помощью пакета «анализ данных» в Excel (пример только для актива А):

Сначала нужно проверить наличие пакета «анализ данных», если не стоит, то установить в файл → параметры → надстройки. Затем в пакете выбираем опцию регрессия и делаем следующие манипуляции, согласно фото

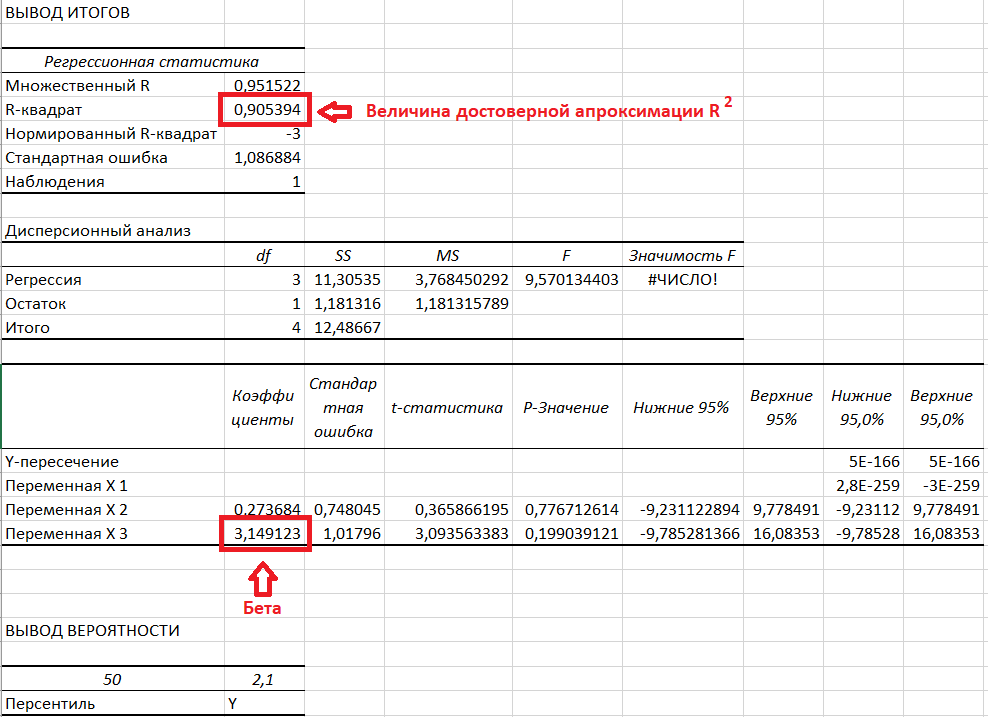
Получаем следующие значения:

Как видим значения сошлись.

Теперь с помощью Excel покажем графическое представление бета:

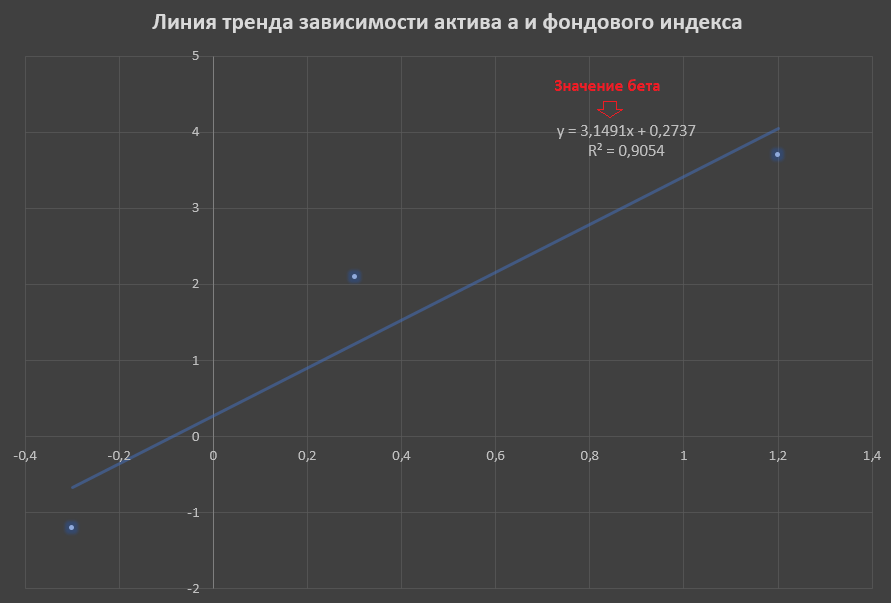
На основании данных, приведенных в таблице значений по месяцам построим точечный график зависимости доходности актива А от фондового индекса (в примере будем делать только для актива А)

По оси Х следует вводить значения доходности индекса, по Y — значения доходностей актива.

Уравнение тренда – это и есть уравнение линейной регрессии, в котором значение 3,1491 — значение бета. Таким образом можно сказать, что бета представляет собой наклон линии тренда. Значение беты показывает, что при повышении фондового индекса на 1, значение актива возрастает на 3,1491.

Бета портфеля, бета – нейтральный портфель.

Бета портфеля показывает совокупный риск вашего собственного портфеля относительно рынка. Важно понимать, как его рассчитать, чтобы составить портфель максимально нетерпимый к риску, а точнее, независимый от рынка.

Формула расчета беты портфеля:

β_п – коэффициент бета портфеля;

Θ_i – вес i-ого актива в портфеле;

β_i – бета i-ого актива в портфеле.

Рассчитаем бету портфеля, в активе которого есть актив А и Б

Возьмем данные из предыдущего примера, для расчетов примем вес актива А в портфеле 10%, актива Б — 90%.

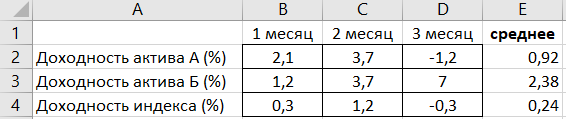
Значение беты портфеля β_п = 3,14·0,1-1,8·0,9 = -1,306

Бета — нейтральный портфель и принципы его составления

Бета-нейтральный портфель, это частный случай, при котором бета портфеля равна нулю

Как же его получить?

Надо включить в портфель в дополнение к бумагам с положительной бетой, бумаги с отрицательной бетой и с такими весами, чтобы при подсчете беты портфеля она получилась равной нулю.

На практике достаточно мало портфелей имеют бету меньше нуля, но практически к ним можно отнести акции золотодобывающих компаний, т.к. в период кризисов они не просто не падают, а показывают существенный рост. (В России – это акций ПАО «Полюс» и ПАО «полиметалл»).

Включить в портфель активы, которые не куплены, а проданы (а точнее, в шорте). Т.к. актив в шорте, то перед бетой надо поставить знак -1.

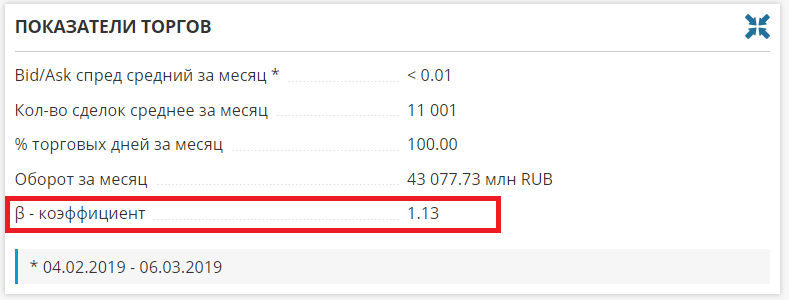
Если нет желания считать бету самостоятельно, то посмотреть ее можно здесь:

Бету всегда можно найти на сайте Московской Биржи, по ссылке:

На сайте investfunds.ru

Недостатки использования беты и их модификации

Как и у любой модели, у методики применения беты есть свои преимущества и недостатки. Многие эксперты пришли к выводу, что для любой акции ее бета не является устойчивым во времени показателем и поэтому не может служить точной оценкой будущего риска.

Для российского рынка характерны следующие недостатки применения модели классической беты:

1) Низкий показатель детерминации. Показывает долю риска, который присущ рыночному риску;

2) Мало информативные значения беты (которые нельзя применять) для акций малой ликвидности и капитализации;

3) Не применим к бумагам, у которых нету исторических цен (на длительном отрезке времени);

4) Коэффициент бета не может предусмотреть реальных положений дел в компаниях.

По всем этим причинам, описанным выше, были выведены модифицированные беты:

Наиболее популярные модификации представлены ниже (2 формулы)

Бета согласно Маршалу Блюму

Его расчеты показали, что со временем величина бета-портфеля приближается к единице, а внутренний риск компании стремится к среднеотраслевому или среднерыночному. Такую бету используют многие инвестиционные банки мира.

β_бл – бета по Маршалу Блюму;

β – коэффициент классической, сырой беты;

Бета согласно Шоулза-Виллимса

β_шв – бета по Маршалу Блюму;

— коэффициенты бета для предыдущего, текущего и последующего периода;

— коэффициент автокорреляции рыночной доходности.

Источник

Коэффициент бета. Формула. Расчет в Excel для ОАО “Газпром”. Современные модификации

Разберем такой инвестиционный показатель как – коэффициент бета, рассчитаем его на реальном пример с помощью Excel и рассмотрим различные современные модификации.

Инфографика: Коэффициент бета

Оценка стоимости бизнеса	Финансовый анализ по МСФО	Финансовый анализ по РСБУ
Расчет NPV, IRR в Excel	Оценка акций и облигаций

Коэффициент бета. Определение

Коэффициент бета (англ. Beta, β, beta coefficient) – определяет меру риска акции (актива) по отношению к рынку и показывает чувствительность изменения доходности акции по отношению к изменению доходности рынка. Коэффициент бета может быть рассчитан не только для отдельной акции, но также и для инвестиционного портфеля. Коэффициент используется как мера систематического риска, и применяется в модели У.Шарпа – оценки капитальных активов CAPM (Capital Assets Price Model). В первые, коэффициент бета рассмотрел Г. Марковиц для оценки систематического риска акций, который получил называние индекс недиверсифицируемого риска. Коэффициент бета позволяет сравнивать между собой акции различных компаний по степени их риска.

Формула расчета коэффициента бета

где:

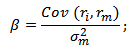
β – коэффициент бета, мера систематического риска (рыночного риска);

r_i – доходность i-й акации (инвестиционного портфеля);

r_m – рыночная доходность;

σ 2 _m – дисперсия рыночной доходности.

★ Excel таблица для формирования инвестиционного портфеля ценных бумаг (рассчитай портфель за 1 минуту) + оценка риска и доходности

★ Программа InvestRatio – расчет всех инвестиционных коэффициентов в Excel за 5 минут (расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR) + прогнозирование движения курса

Анализ уровня риска по значению коэффициента бета (β)

Коэффициент бета показывает рыночный риск акции и отражает чувствительность изменения акции по отношению к изменению доходности рынка. В таблице ниже показана оценка уровня риска по коэффициенту бета. Коэффициент бета может иметь как положительный, так и отрицательный знак, который показывает положительную или отрицательную корреляцию между акцией и рынком. Положительный знак отражает, что доходность акций и рынка изменяются в одном направлении, отрицательный ­– разнонаправленное движение.

Значение показателя

Уровень риска акции

Направление изменения доходности акции

-1 Низкий

Данные для построения коэффициента бета информационными компаниями

Коэффициент бета используется многими информационно-инвестиционными компаниями для оценки систематического риска: Bloomberg, Barra, Value Line и др . Для построения коэффициента бета используются месячные/недельные данные за несколько лет. В таблице показаны основные параметры оценки показателя различными информационными компаниями.

Информационные компании

Исторический период наблюдения Частота

Можно заметить, что Bloomberg проводит краткосрочную оценку показателя, тогда как Barra и Value Line используют месячные данные доходностей акций и рынка за последние пять лет. Долгосрочная оценка может сильно быть искажена вследствие влияния на акции компании различных кризисов и негативных факторов.

Коэффициент бета в модели оценки капитальных активов – CAPM

Формула расчета доходности акций по модели капитальных активов CAPM (Capital Assets Price Model, модель У.Шарпа) имеет следующий вид:

где:

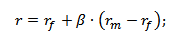
r – будущая ожидаемая доходность акций компании;

r_f – доходность по безрисковому активу;

r_m – доходность рынка;

β – коэффициент бета (мера рыночного риска), отражает чувствительность изменения стоимости акций компании в зависимости от изменения доходности рынка (индекса);

Модель CAPM была создана У.Шарпом (1964) и Дж. Линтером (1965) и позволяет спрогнозировать будущее значение доходности акции (актива) на основании линейной регрессии. Модель отражает линейную взаимосвязь планируемой доходности с уровнем рыночного риска, выраженного коэффициентом бета.

Доходность по безрисковому активу, на практике, берется как доходность по государственным ценным бумагам ГКО, ОФЗ. Доходность по ним в России составляет около 12%. Доходность можно посмотреть на сайте ЦБ в разделе «Ставки рынка ГКО-ОФЗ».

Для расчета рыночной доходности используют доходность индекса или фьючерса на индекс (индекс ММВБ, РТС ­– для России, S&P500 – США).

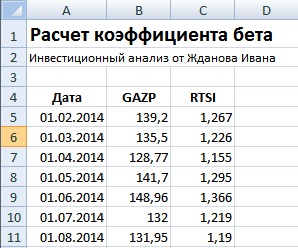
Пример расчета коэффициента бета в Excel

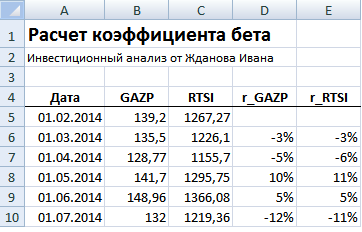
Рассчитаем коэффициент бета в Excel для отечественной компании ОАО «Газпром». Данная компания имеет обыкновенные акции, котировки которых можно посмотреть на сайте finam.ru в разделе «Экспорт данных». Для расчета были взяты месячные котировки акции ОАО «Газпром» (GAZP) и индекса РТС (RTSI) за период с 31.01.2014 по 31.01.2015 г.

Далее необходимо рассчитать доходности по акции и индексу, для этого воспользуемся формулами:

Для расчета коэффициента бета необходимо рассчитать коэффициент линейной регрессии между доходностью акций ОАО «Газпром» и индекса РТС. Рассмотрим два варианта расчета коэффициента бета средствами Excel.

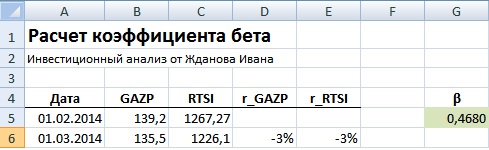
Вариант №1. Расчет через формулу Excel

Расчет через формулы Excel выглядит следующим образом:

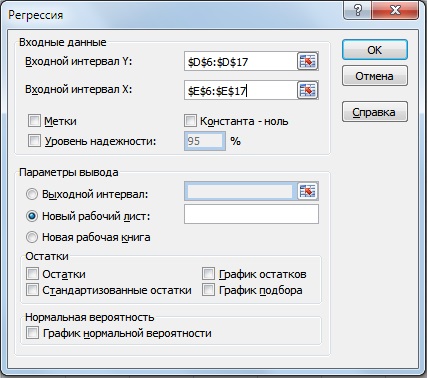
Вариант №2. Расчет через надстройку «Анализ данных»

Второй вариант расчета коэффициента бета использует надстройку Excel «Анализ данных». Для этого необходимо перейти в главном меню программы в раздел «Данные», выбрать опцию «Анализ данных» (если данная надстройка включена) и в инструментах анализа выделить «Регрессия». В поле «Входной интервал Y» выбрать доходности акции ОАО «Газпром», а в поле «Выходные интервал X» выбрать доходности индекса РТС.

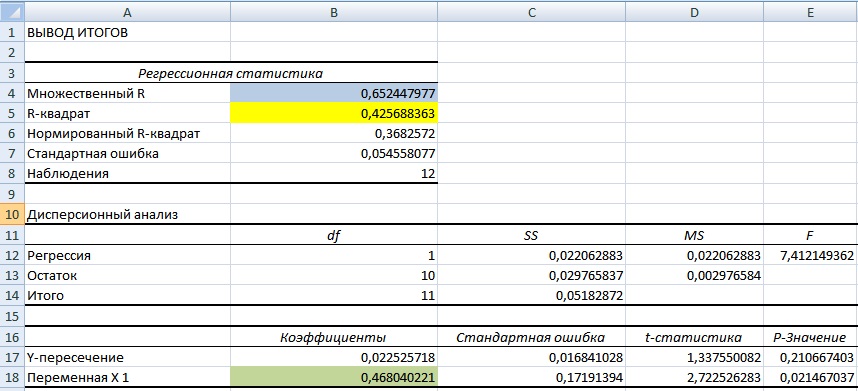
Далее мы получим отчет по регрессии на отдельном листе. В ячейке В18 показано значение коэффициента линейной регрессии, который равен коэффициенту бета = 0,46. Также проанализируем другие параметры модели, так показатель R-квадрат (коэффициент детерминированности) показывает силу взаимосвязи между доходностью акции ОАО «Газпром» и индекса РТС. Коэффициент детерминированности равен 0,4, что является довольно мало для точного прогнозирования будущей доходности по модели CAPM. Множественный R – коэффициент корреляции (0,6), который показывает наличие зависимости между акцией и рынком.

Значение 0,46 коэффициента бета для акции свидетельствует о умеренном риске и в тоже время сонаправленность изменения доходностей.

★ Программа InvestRatio – расчет всех инвестиционных коэффициентов в Excel за 5 минут (расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR) + прогнозирование движения курса

Недостатки использования коэффициента бета в модели CAPM

Рассмотрим ряд недостатков присущих данному коэффициенту:

1. Сложность использования коэффициента бета для оценки низколиквидных акций. Данная ситуация характерна для развивающихся рынков капитала, в частности: России, Индии, Бразилии и т.д.
2. Не возможность оценки малых компаний, не имеющих эмиссий обыкновенных акций. Большинство отечественных компаний не проходили процедуры IPO.
3. Неустойчивость прогноза коэффициента бета. Использование линейной регрессии для оценки рыночного риска по ретроспективным данным не позволяет получать точные прогнозы риска. Как правило, трудно прогнозировать коэффициент бета более 1 года.
4. Не возможность учета несистематических рисков компании: рыночной капитализации, исторической доходности, отраслевой принадлежности, критериев P/E и т.д., которые оказывает влияние на величину ожидаемой доходности.

Модификация коэффициента бета

Так как коэффициент, предложенный У. Шарпов не имел должной устойчивости и не мог использоваться для прогнозирования будущей доходности в модели CAPM, различными учеными были предложены модификации и корректировки данного показателя (англ. adjusted beta, modified beta).Рассмотрим скорректированные коэффициенты бета:

Модификация коэффициента бета от М.Блюма (1971)

Маршал Блюм показал, что со временем коэффициенты бета компаний стремятся к 1. Формула расчета скорректированного показателя следующая:

Использование данных весовых значений позволяет более точно спрогнозировать будущий систематический риск. Так данную модификацию используют многие информационные агентства, такие как: Bloomberg, Value Line и Merrill Lynch.

Модификация коэффициента бета от Бава-Линдсберга (1977)

В своей корректировке Линдсберг предложил рассчитывать односторонний коэффициент бета. Главный постулат заключался в том, что изменение доходности выше определенного уровня большинство инвесторов не рассматривают как риск, а риском считается только то, что ниже уровня. За минимальный уровень риска в данной модели был доходность безрискового актива.

где:

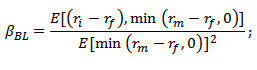
r_i – доходность акции; r_m – доходность рынка; r_f – доходность безрискового актива.

Модификация коэффициента бета от Шоулза-Виллимса

β_-1, β, β₁ – коэффициенты беты для предыдущего (-1) текущего и следующего (1) периода;

ρ_m – коэффициент автокорреляции рыночной доходности.

Модификация коэффициента бета от Харлоу-Рао (1989)

Формула отражает одностороннюю бету, с предположением, что инвесторы рассматривают риск только как отклонение от среднерыночной доходности вниз. В отличие от модели Бава-Линдсберга за минимальный уровень риска брался уровень среднерыночной доходности.

где: μ_i – средняя доходность акции; μ_m – средняя доходность рынка;

Помимо коэффициента бета на практике используют другие показатели риска-доходности инвестиционного портфеля, ПИФа, более подробно узнать про современные показатели оценки инвестиций вы можете в моей статье: “Оценка эффективности инвестиций, инвестиционного портфеля, акций на примере в Excel“. О практике оценке риска инвестиции читайте в статье: “Методы оценки риска VaR (Value at Risk). Рыночный риск. Пример расчета в Excel “.

Коэффициент бета для акций США

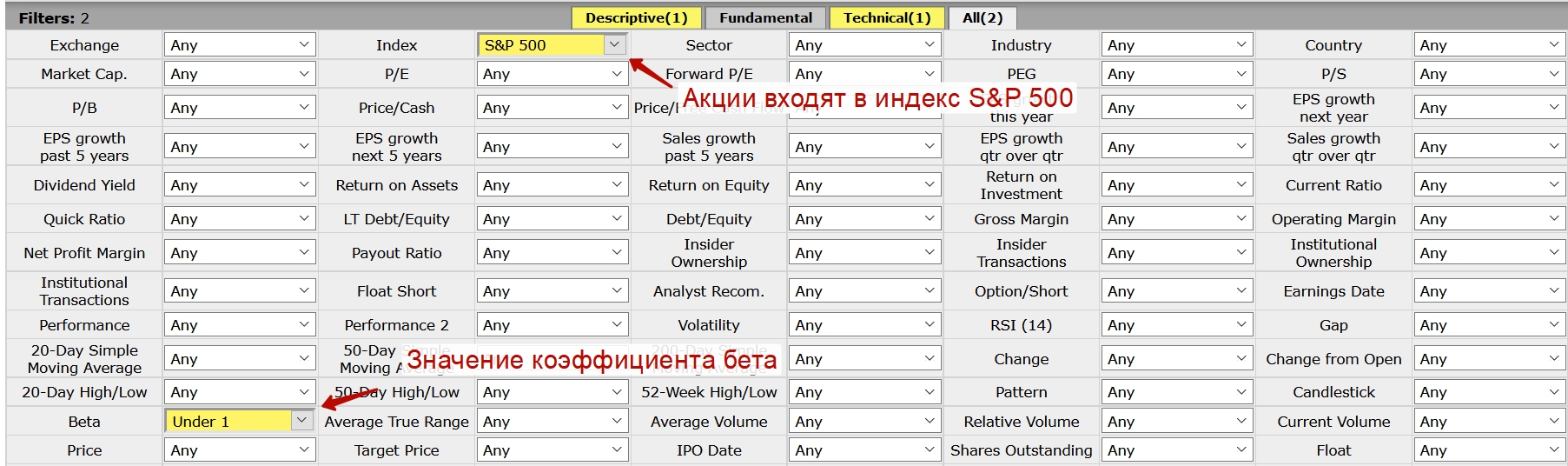
Существуют сервисы позволяющие оценить коэффициент бета для множества компаний и выделить наиболее интересные. Будем применять сервис Finviz. Чтобы найти акции менее чувствительные чем колебания фондового рынка необходимо установить коэффициент бета меньше 1.

Фильтрация акций США по бета меньше “1” позволяет найти акции для консервативного инвестора, изменчивость которых ниже изменения индекса S&P 500

Где посмотреть коэффициент бета для российских акций

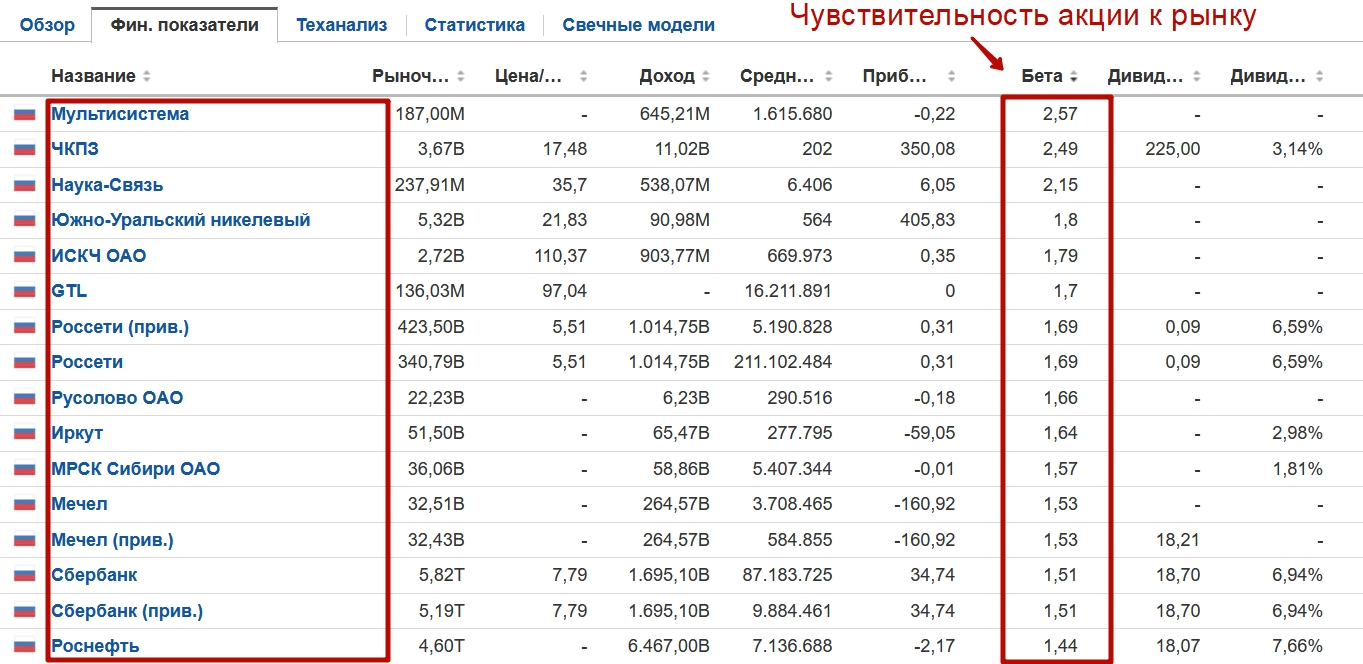
Если цель узнать коэффициент бета для российских акций, то для этого можно воспользоваться сервисом investing.com. Помимо отечественных компаний коэффициент бета можно определить для иностранных. Как мы видим для акции Мультисистемы коэффициент равен 2,57 – это значит, что она в 2,5 раза более изменчивая по отношению к рыночному изменению (индексу ММВБ).

Проанализировать акции на бета можно по ссылке.

Сортировка отечественных акций по коэффициента бета. Чем выше значение тем более изменчива акция по отношению к индексу ММВБ

Высокие значения коэффициента бета при растущем рынке будут обеспечивать дополнительную прибыль, при коррекциях такие акции как правило имеют больше убытков.

Резюме

Коэффициент бета является одним из классических мер рыночного риска для оценки доходности акций, инвестиционных портфелей и ПИФов. Несмотря на сложность использования данного инструмента для оценки отечественных низколиквидных акций и неустойчивость его изменения во времени, коэффициент бета является ключевым показателем оценки инвестиционных рисков. Рассмотренные модификации коэффициента позволяют скорректировать и дать более оценку систематическому риску. С вами был Иван Жданов, спасибо за внимание.

Автор: к.э.н. Жданов Иван Юрьевич

Источник