Банк выплачивает по вкладам 10 годовых сложных какова реальная доходность вкладов

Калькулятор доходности вкладов

Онлайн калькулятор вкладов поможет вам быстро рассчитать проценты по любому вкладу, в том числе с капитализацией, с пополнениями и с учетом налогов, а также покажет график начисления процентов. Если вы планируете открыть вклад, то калькулятор поможет вам заранее рассчитать потенциальную доходность.

Капитализация процентов

При обычном вкладе начисленные проценты банк выплачивает вкладчику ежемесячно (либо с другой периодичностью, оговоренной условиями договора). Это называется «простые проценты». Вклад с капитализацией (или «сложные проценты») — это условие, при котором начисленные проценты не выплачиваются, а прибавляются к сумме вклада, таким образом увеличивая её. Общий доход от вклада в этом случае будет выше.

С помощью депозитного калькулятора вы можете сравнить результаты расчёта двух одинаковых вкладов (с капитализацией и без) и увидеть разницу.

Эффективная процентная ставка по вкладу

Эта характеристика актуальна только для вкладов с капитализацией процентов. В связи с тем, что проценты не выплачиваются а идут на увеличение суммы вклада, очевидно, что если ежемесячно возрастает сумма вклада, то и вновь начисленные на эту сумму проценты также будут выше, как и конечный доход.

Если рассчитать, сколько процентов было начислено к начальной сумме к концу срока вклада, эта величина и будет являться эффективной процентной ставкой.

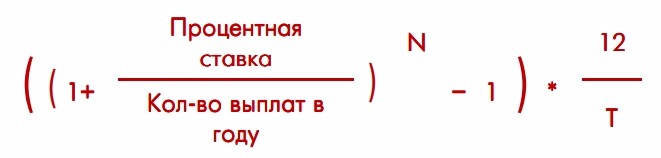
Формула расчета эффективной ставки:

где
N — количество выплат процентов в течение срока вклада,
T — срок размещения вклада в месяцах.

Эта формула не универсальна. Она подходит только для вкладов с капитализацией 1 раз в месяц, период которых содержит целое количество месяцев. Для других вкладов (например вклад на 100 дней) эта формула работать не будет.

Однако есть и универсальная формула для рассчета эффективной ставки. Минус этой формулы в том, что получить результат можно только после рассчета процентов по вкладу.

Эта формула подходит для всех вкладов, с любыми сроками и любой периодичностью капитализации. Она просто считает отношение полученного дохода к начальной сумме вклада, приводя эту величину к годовым процентам. Лишь небольшая погрешность может присутствовать здесь, если период вклада или его часть выпала на високосный год.

Именно этот метод используется для рассчета эффективной ставки в представленном здесь депозитном калькуляторе.

Налог на доход по вкладам

Как было до 2021 года

Налог начислялся в случаях, если ставка по вкладу превышала ключевую на 5 и более процентов. Размер налога был 35% и 30% для резидентов и нерезидентов соответственно. Начислялся он не на весь доход во вкладу, а только на разницу между доходом, вычисленным по пороговой ставке (ключевая ставка + 5%) и реально полученным доходом.

Как стало с 2021 года

• Налоговая ставка теперь 13% для всех.
• Введена необлагаемая сумма дохода. Все, что выше — облагается налогом. Количество вкладов не имеет значения, считается общая сумма на всех вкладах.
• Необлагаемый доход рассчитывается следующим образом:

В качестве примера возьмем 2021 год.

1. У Васи есть 2 вклада в разных банках. В первом банке 500 000 руб. под 5%, во втором банке 800 000 руб под 4%.
2. Ключевая ставка ЦБ на 1 января 2021 года была 4.25%.
3. Сумма необлагаемого дохода едина для всех вкладов и составляет 1 000 000 × 4.25% = 42 500 руб. С этой суммы налог платить не нужно.
4. Доход по вкладам васи за год составит: в первом банке — 25 000 руб., во втором — 32 000 руб. Всего — 57 000 руб.
5. Разница между фактическим и необлагаемым доходом составит 57 000 — 42 500 = 14 500 руб. Это тот доход, с которого необходимо заплатить НДФЛ.
6. Размер НДФЛ = 14 500 × 13% = 1 885 руб.

Наш депозитный калькулятор рассчитывает вклады с учетом налогов.

Источник

Задача 7. Банк в конце года выплачивает по вкладам 10% годовых

Банк в конце года выплачивает по вкладам 10% годовых. Какова реальная доходность вкладов при начислении процентов: а) ежеквартально; б) по полугодиям.

Ответ.

а) i = (1+ ) 4 – 1 = 0,1038, т. е. 10,38 %;

б) i = (1+ ) 2 – 1 = 0,1025, т. е. 10,25 %.

Расчет показывает, что разница между ставками незначительна, однако начисление 10 % годовых ежеквартально выгодней для вкладчика.

Задача 8.

В первый год на сумму 10 000 ден.ед. начисляются 10 % годовых, во второй – 10,5 % годовых, в третий – 11 % годовых. Определить сумму погашения, если проценты выплачиваются ежегодно.

Ответ.

Расчет наращенной суммы при изменении процентной ставки во времени с начислением простых процентов.

где i_n – ставка простых процентов, t_n – продолжительность периода начисления.

S = 10 000 (1+0,10 · 1 +0,105 · 1 + 0,11 · 1)=13 150, ден.ед.;

ДР = 3 150 ден.ед.

Задача 9.

В первый год на сумму 10 000 ден.ед. начисляются 10 % годовых, во второй – 10,5 % годовых, в третий – 11 % годовых. Определить сумму погашения, если проценты капитализируются.

Ответ.

При начислении сложных процентов применяется формула

где i_n – ставка сложных процентов, t_n – продолжительность периода ее начисления.

S = 10 000 (1+0,10 · 1)·(1 +0,105 · 1)·(1 + 0,11 · 1)= 13 492, 05, ден.ед.

Источник

Финансовая математика (стр. 15 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

Эффективная процентная ставка — годовая ставка сложных процентов, которая дает тот же результат, что и начисление по номинальной ставке m раз в год.

Эффективная учетная ставка характеризует результат дисконтирования за год и находится путем приравнивания множителей дисконтирования по годовой учетной ставке и по номинальной учетной ставке m раз в год

Эффективная процентная ставка

Эффективная учетная ставка

Следует отметить, что при прочих равных условиях эффективная учетная всегда ставка меньше или равна номинальной.

Фирма планирует получение кредита в сумме 1 млн. руб. Банк предоставляет кредит под 20% годовых простых. На какой срок фирма может взять кредит с тем, чтобы подлежащая возврату сумма не превысила 1,4 млн. руб.

года

Ответ: фирма может взять кредит на 2 года.

На какой срок фирма может взять кредит в банке в размере 2 млн. руб. с условием, чтобы сумма возврата долга не превысила 2,2 млн. руб., если банк применит ставку 19% годовых простых, при K=365 дней?

дня

Ответ: фирма может взять кредит на 192 дня.

Фирма получила ссуду в банке в размере 800 тыс. руб. сроком на полгода. Сумма погашения составляет 900 тыс. руб. Определить процентную ставку, примененную банком.

Ответ: процентная ставка, примененная банком, составляет 25%.

Сберегательный сертификат куплен за 100 тыс. руб., выкупная его сумма 160 тыс. руб., срок 2,5 года. Каков уровень доходности инвестиций в виде годовой ставки сложных процентов?

Ответ: уровень доходности составляет 20,68%.

За какой срок в годах сумма, равная 75 млн. руб. достигнет 200 млн. руб. при начислении процентов по сложной ставке 15% раз в году и поквартально?

1)

2)

Ответ: 7,0178 лет, 6.6607 лет.

Какова эффективная ставка процентов, если номинальная ставка равна 35 % при помесячном начислении процентов.

Ответ: Эффективная ставка процентов равная 41,2% в год приводит к тем же финансовым результатам, что и ставка процентов равная 35% с капитализацией раз в месяц.

Банк выплачивает по вкладам 10% годовых сложных. Какова реальная доходность вкладов в этом банке при следующих видах начисления процентов: а) ежемесячно, б) ежеквартально, в) по полугодиям, г) непрерывно?

а)

б)

в) .

г)

5. Эквивалентность финансовых операций в случаях простой и сложной процентной ставке

Замена одного вида ставки (процентной или учетной) на другой при соблюдении принципа эквивалентности не изменит финансовых результатов. Такие ставки называются эквивалентными.

Формулы эквивалентности всегда получаются путем приравнивания соответствующих множителей наращения и решения полученного уравнения.

Определить значение учетной ставки банка, эквивалентной ставке простых процентов 35 % годовых.

Ответ: Учетная ставка, эквивалентная ставке простых процентов равна 23,9%

Определить величину силы роста при начислении непрерывных процентов в течение года, эквивалентную учетной ставке простых процентов 15%.

Ответ: сила роста, эквивалентная учетной ставке простых процентов 16,2519%.

Срок оплаты долгового обязательства составляет полгода по простой учетной ставке 40% годовых. Оцените доходность операции по эквивалентным ставкам (считать, что номинальная ставка начисляется ежеквартально).

1) эквивалентная простая ставка:

2) эквивалентная ставка сложных процентов:

3) эквивалентная номинальная ставка сложных процентов:

4) эквивалентная сложная учетная ставка:

5) эквивалентная номинальная учетная ставка:

6. Наращение сложных и простых процентов с учетом инфляции

Инфляция— снижение реальной покупательной стоимости денег за период, охватываемый финансовой операцией.

Будем использовать следующие обозначения:

S— наращенная сумма по номиналу; C— наращенная сумма с учетом обесценивания;

индекс покупательной способности ( 1):

h — темп инфляции (относительный прирост цен за период (%)):

— среднегодовой темп роста цен:

H — среднегодовой темп инфляции:

Индекс цен за несколько периодов:

Если ,то (k-общее число периодов)

барьерная ставка процентов (ставка процентов, выше которой будет приносить, в условиях данных показателей инфляции, реальный доход.)

— брутто — ставка (ставка процентов, обеспечивающая реальную доходность финансовой операции в условиях инфляции)

Перечисленные параметры связаны между собой соотношениями, представленными в таблице:

Источник