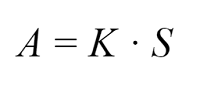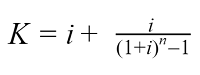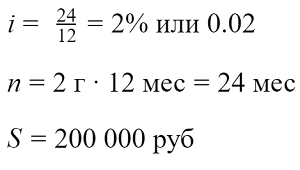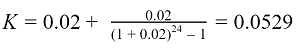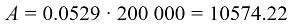Аннуитет это инвестиции расчет

Аннуитет по кредиту — что это?

Тенденции развития современного общества привели к тому, что те понятия, которые не так давно использовались главным образом в учебниках по экономической теории, стали все чаще встречаться в повседневной жизни. Одним из таких терминов является аннуитет, который все более активно стали использовать в сфере кредитования. Данный инструмент является достаточно выгодным, поэтому есть смысл познакомиться с его отличительными особенностями и способами расчета более подробно. Об этом и пойдет речь в данной статье.

Что такое аннуитет?

Аннуитет это — схема платежей, в соответствие с которой они производятся в одинаковом размере в соответствие с конкретным графиком выплат (а именно на постоянной основе через равные промежутки времени). Таким образом, можно представить аннуитет как поток одинаковых платежей, которые осуществляются через равные временные интервалы.

По аннуитетному виду платежа предполагается что выплаты осуществляются равными суммами через равные промежутки времени. Сумма аннуитетного платежа состоит из двух частей:

• Процентная часть, которая идет на оплату процентов пользования заемными средствами.
• Остаточная часть, которая направляется на оплату основного долга по кредиту.

Аннуитет позволяет сделать величину платежа, который включает в себя не только проценты за период, но и часть основного долга, постоянной. Это дает возможность плательщику заранее оценить свои силы и запланировать выплаты определенной суммы денежных средств в течение оговоренного срока.

Основным отличием от так называемого дифференцированного платежа является то, что при использовании последнего в первую очередь выплачивается полная сумма начисленных за использование кредитных средств процентов, а потом уже основной долг.

Отметим, что принцип аннуитета используется не только в кредитовании, но и для лизинговых платежей.

Какие выделяют виды аннуитета?

Для лучшего понимания использования аннуитета следует рассмотреть, какие его виды существуют. Так, можно отметить наличие следующей классификации:

• отложенный – в данном случае первая выплата производится в конце начального периода;
• немедленный – платеж осуществляется в начале нулевого периода.

Если говорить об аннуитете, используемом в сфере кредитования, то здесь имеет место отложенный аннуитет.

Кроме этого, распространенно выделение различных видов стоимости аннуитета, а именно:

• приведенная;
• будущая стоимость аннуитета.

Такое деление обусловлено стремлением определить максимально объективную ценность денежных средств, которые направлены на кредитование. Как будущая, так и текущая стоимость аннуитета рассчитывается определенным образом с использованием конкретных формул. Проводимый расчет текущей стоимости аннуитета зависит от ряда факторов.

Стоит отметить, что в силу теории о том, что с течением времени денежные средства могут обесцениваться в силу инфляции, имеет место такое понятие, как настоящая стоимость аннуитета. Также здесь играет роль упущенная выгода, ведь если бы кредитор оставил выданные денежные средства у себя, то он имел бы возможность получать доход в виде процентов по вкладу.

Формула расчета аннуитетного платежа

Формула аннуитетного платежа:

• A – ежемесячный аннуитетный платеж;
• K – коэффициент аннуитета;
• S – сумма кредита.

Расчет коэффициента аннуитета:

• K – коэффициент аннуитета;
• i – месячная процентная ставка по кредиту (годовая ставка деленная на 12 месяцев);
• n – количество периодов (месяцев), в течение которых выплачивается кредит.

Знание рассмотренной формулы позволяет провести требуемые расчеты, которые при наличии полных исходных данных не представляют собой особых сложностей. Очевидно, что для применения ее на практике необходимо учитывать некоторые принципиальные моменты. В их числе можно отметить, в первую очередь, принцип, по которому определяются доли основного долга и начисленных процентов в итоговом размере платежа. Для этого применяется определенная методика, которая предполагает прохождение несколько этапов расчета. Мы не будем на ней подробно останавливаться, отметим лишь общий принцип, в соответствии с которым производится расчет размера процентов и аннуитетного платежа, так же как и основного долга в виде разницы между этими двумя величинами для каждого месяца периода. При этом учитывается, что размер основного долга от месяца к месяцу снижается. Последний платеж требует отдельной корректировки в силу применения в процессе расчетов округлений.

Несмотря на равную величину платежей, соотношение суммы основного долга и начисленных процентов в их составе меняется. Если в начале основная доля приходится на проценты, то ближе к концу выплат остается погасить главным образом основную сумму долга.

Пример расчета аннуитетного платежа

Рассчитаем ежемесячный платеж по кредиту с аннуитетным графиком погашения под процентную ставку 24% годовых сроком на 2 года и на сумму 200 000 рублей.

Воспользуемся приведенными выше формулами:

Рассчитаем коэффициент аннуитета:

Теперь мы можем приступить к расчеты самого ежемесячного платежа. Подставим полученное значение коэффициента аннуитета:

Сумма ежемесячного платежа составила 10574.22 рублей.

Переплата по кредиту

Всего за 2 года банку будет выплачено 253 781.3 руб (10574.22 руб умноженные на 24 мес), а переплата составит 53781.3 руб.

Рассчитать кредит можно с помощью калькулятора кредита на нашем сайте.

Источник

Аннуитет и финансовая рента в инвестициях

В большинстве коммерческих операций вместо разовых платежей встречается последовательность денежных поступлений или выплат. Серия потоков поступлений или выплат называется потоком платежей . Поток однонаправленных платежей с равными интервалами времени между последовательными платежами в течение определенного количества лет представляет собой аннуитет (финансовая рента) .

Денежные поступления при оценке долговых и долевых ценных бумаг, возможных арендных платежей можно представить следующим образом:

Аннуитеты могут подразделяться по количеству выплат в году, т. е. годовые выплаты (1 раз в год) и срочные (ряд выплат в пределах года), а также по количеству начислений процентов в течение года (ежегодно несколько раз в год или непрерывно).

По времени наступления платежей различают два типа аннуитета:

1. Обыкновенный (постнумерандо) аннуитет — когда платежи происходят в конце каждого периода.

2. Авансовый (пренумерандо) аннуитет — когда платежи происходят в начале каждого периода.

По продолжительности денежного потока различают:

3. Срочный аннуитет — денежный поток с равными поступлениями в течение ограниченного промежутка времени.

Примером срочного аннуитета постнумерандо являются арендные платежи, за пользование имуществом, землей и т. п., которые регулярно поступают по истечении очередного периода. В качестве примера срочного аннуитета пренумерандо можно представить схему периодических денежных вкладов на банковский счет в начале каждого месяца с целью наполнения определенной суммы, необходимой для решения конкретной задачи.

1. Бессрочный аннуитет — когда денежные поступления продолжаются достаточно длительное время.

Будущая стоимость обыкновенного аннуитета

Будущая стоимость обыкновенного аннуитета рассчитывается по следующей формуле:

где — денежные поступления аннуитета; — коэффициент наращения будущей стоимости аннуитета.

Для денежного потока из периода будущая стоимость авансового аннуитета равна:

Для определения суммы, которую необходимо депонировать в конце каждого периода для того, чтобы через заданное число периодов остаток составил необходимую величину, используется функция, называемая фактор фонда возмещения :

Данный фактор учитывает процент, получаемый по депозитам. Сумма ежегодного вклада составит:

где — стоимость поступлений по истечении срока вложений.

Формула (1.17) применяется для определения суммы, которую следует ежегодно вкладывать на депозитный счет в банк, чтобы через определенное количество лет получить заданную стоимость.

Часто в тех случаях, когда вплоть до истечения срока кредитного договора (долгового обязательства) кредитору выплачивается только процент, заемщики для погашения основной суммы кредита создают специальные фонды возмещения. В каждый период должник вносит в отдельный фонд сумму, которая вместе с начисляемым на нее процентом должна обеспечить погашение основной части кредита.

Пример 3. Чтобы получить 800 тыс. руб. в конце четырехлетнего периода при нулевом проценте, необходимо депонировать тыс. руб. Если процентная ставка составит 10 %, тогда можно депонировать

Разница четырех взносов (524,2 тыс. руб.) и полученной суммы составит 275,8 тыс. руб.

Настоящая и текущая стоимость обыкновенного аннуитета

Настоящая стоимость обыкновенного аннуитета для денежного потока из периодов рассчитывается по формуле:

Отдельные элементы денежного потока относятся к разным временным интервалам, поэтому их суммирование искажает реальную доходность инвестиций. Приведение денежного потока к одному моменту времени осуществляется при помощи функции, называемой текущей стоимостью аннуитета.

Текущая стоимость обыкновенного аннуитета определяется по формуле:

где — коэффициент дисконтирования настоящей стоимости аннуитета.

Пример 4. В результате осуществления инвестиционного проекта ежегодные доходы в течение 5 лет будут составлять по 500 тыс. руб.

Текущая стоимость денежных потоков составит:

В результате дисконтирования дохода за каждый период получим:

В тех случаях, когда денежные поступления приходят в начале периода, настоящая стоимость авансового аннуитета для денежного потока из периодов рассчитывают следующим образом:

Формула (1.20) применяется для определения текущей стоимости, если доходы, получаемые за каждый i-й период, равны. При неравенстве доходов по временным периодам их получения рассчитывается дисконтированная стоимость за каждый период.

Функция погашения кредита

Для определения дохода, который необходимо получать ежегодно, чтобы возместить (окупить) инвестиции за определенный период времени с учетом процентной ставки, используется функция погашения кредита :

Формула (1.21) применяется для определения суммы, которую необходимо ежегодно (ежеквартально) вносить в банк для погашения кредита и процентов по нему.

Ежегодный доход (аннуитет) определяется умножением суммы инвестиций на множитель

где — начальная сумма инвестиции (вложений).

Пример 5. Инвестиции в проект составили 900 тыс. руб. Чтобы окупить инвестиции в течение 5 лет и получить доход в размере 10 % годовых, ежегодный денежный поток (аннуитет) должен составить:

Настоящая стоимость бессрочного аннуитета

Настоящая стоимость бессрочного аннуитета определяется по формуле:

Бессрочным называется такой денежный поток, при котором денежные поступления продолжаются весьма длительное время (например, аренда на 50 лет и более).

Формула (1.23) показывает максимальную цену, которую инвестор согласен заплатить за бессрочные денежные поступления. Для этого в числителе используют размер годовых поступлений, а в знаменателе в качестве коэффициента дисконтирования обычно принимается гарантированная процентная ставка (например, процент по государственным ценным бумагам).

Источник

Формула аннуитетного платежа, расчет платежа

Когда вы берёте в банке кредит, вы обязуетесь в течение определённого срока выплачивать сумму взятого кредита и процентов по нему. Существует несколько способов погашения кредита, распространённый способ — это аннуитетные платежи. В этой статье мы рассмотрим, что такое аннуитетные платежи, узнаем формулу аннуитетного платежа и проведём расчёт.

Аннуитетный и дифференцированный платёж

Аннуитет — это одинаковый по сумме ежемесячный платёж. То есть при аннуитетном платеже вы каждый месяц платите одинаковую сумму (кредит + проценты по нему) независимо от оставшейся суммы задолженности.

Другой способ погашения кредита — это дифференцированный платёж, то есть выплата процентов на оставшуюся задолженность. При дифференцированных платежах ваша сумма ежемесячных выплат будет уменьшаться к концу срока кредита, поскольку вы будете выплачивать проценты за кредит на оставшуюся сумму задолженности. Например, погасив 80% кредита, вы будете платить проценты за оставшуюся сумму (20%).

Для самих банков выгоднее применять аннуитетные платежи, поскольку в этом случае они получают больше прибыли по процентам. Заемщикам же аннуитетные платежи выгоднее в том плане, что удобнее каждый месяц платить одну и ту же сумму, чем каждый раз разную и уточнять, сколько же ему надо внести в следующий месяц.

Формула аннуитетного платежа

В соответствии с формулой аннуитетного платежа размер периодических (ежемесячных) выплат будет составлять:

A = K · S

где А — ежемесячный аннуитетный платёж,
К — коэффициент аннуитета,
S — сумма кредита.

Коэффициент аннуитета рассчитывается по следующей формуле:

где i — месячная процентная ставка по кредиту (= годовая ставка / 12),
n — количество периодов, в течение которых выплачивается кредит.

Поскольку периодичность платежей по кредиту — ежемесячно, то ставка по кредиту (i) берётся месячная. Если процентная ставка 12% годовых, то месячная ставка:
i = 12% / 12 мес = 1%.

С помощью приведённой выше формулы аннуитетного платежа вы можете узнать ежемесячную сумму, которую нужно платить, чтобы погасить кредит.

Расчет аннуитетного платежа

Приведём пример расчета аннуитетного платежа.
Допустим, вы взяли в банке кредит на сумму 30 000 рублей под 18% годовых сроком на 3 года.

Исходные данные:
S = 30 000 рублей
i = 1,5% (18% / 12 мес) = 0,015
n = 36 (3 года х 12 мес)

Подставляем эти значения в формулу и определяем коэффициент аннуитета:

К =	0,015*(1+0,015) 36	= 0,03615
(1+0,015) 36 — 1

Размер ежемесячных выплат:

A = K*S = 0,03615 * 30000 = 1084,57 рублей.

Расчет аннуитетного платежа в Microsoft Excel

Если у вас возникают проблемы с ручным расчётом аннуитетных платежей — можно вычислить в Excel. В Экселе есть специальная функция ПЛТ. Просто создаёте новую таблицу и в любой ячейке вводите строку.

Подставим те же исходные данные, что и в примере, рассмотренном выше. В результате в Экселе нужно ввести следующее выражение:

=ПЛТ(18%/12; 36; -30000)

В скобках формулы указывается по порядку: процентная ставка, количество месяцев, сумма кредита. Можно также записать так:

=ПЛТ(0,015; 36; -30000)

18% годовых / 12 месяцев / 100 = 0,015

В любом случае у нас сумма ежемесячных платежей получится 1084,57 рублей.

Источник