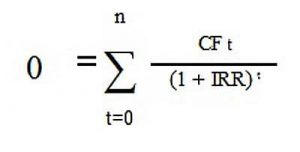Анализ показателя внутренней нормы доходности проекта

Расчет внутренней нормы доходности

Ни один инвестор не вкладывает средства слепо, не проведя предварительных исследований: он должен быть уверен, что они окупятся или, как минимум, их удастся вернуть. Для этого оценивается потенциальная рентабельность инвестиционного проекта. Конечно, это нельзя сделать иначе как комплексно, применяя ряд специально разработанных показателей, важнейший из которых – внутренняя норма доходности.

Рассмотрим, в чем особенности метода инвестиционных исследований, основанного на вычислении внутренней нормы доходности – IRR.

Что такое внутренняя норма доходности?

Никто не может рассчитать с вероятностью 100%, какой доход удастся получить от вложенных средств. Слишком много переменных факторов, могущих повлиять на реализацию бизнес-проекта, профинансированного инвестором. Однако можно максимально снизить риск неточностей, если применить не абсолютную, а относительную оценку.

Та процентная ставка, при которой инвестор гарантированно возместит свое вложение, но не получит прибыли, называется внутренней нормой доходности (ВНД). Норма заключается в том, что все денежные потоки данного инвестиционного проекта в сумме взаимозачтутся. Иначе говоря, расходы на инвестиционный проект в какой-то момент времени уравновешиваются полученными доходами (говорят, что проект «вышел в ноль»).

ВАЖНО! Слово «внутренняя» в определении данной нормы инвестиционных вложений означает ее зависимость от свойств самого проекта, а не от внешних факторов.

Внутреннюю норму доходности специалисты могут именовать по-разному. Встречаются следующие наименования:

• ВНД – русская аббревиатура;
• IRR – английская аббревиатура от «Internal Rate of Return» – «внутренняя норма доходности»;
• внутренняя норма рентабельности;
• внутренняя норма прибыли;
• внутренняя норма возврата инвестиций;
• предельная эффективность капитальных вложений;
• процентная норма прибыли;
• дисконтированный поток реальных денег;
• финансовая норма прибыли;
• собственная норма прибыли.

ВНИМАНИЕ! Эту норму можно счесть предельной, поскольку выход за ее пределы уже означает для инвестора убыток.

Показатели для расчета IRR

Математически расчет внутренней нормы доходности не так уж сложен, но формула включает много дополнительных показателей, которые необходимо учитывать. Среди них:

• NPV – от первых букв выражения «Net Present Value» («чистая приведенная стоимость») – сумма всех денежных потоков данного проекта, приведенная к общему показателю при взаимозачете доходов и затрат;
• CF – денежные потоки (от «Cash Flows») – величины различных притоков и оттоков финансов, в том числе и инвестируемых средств, в выбранный период времени t (обычно берется год). Для инвестиционного проекта первый денежный поток – сама инвестиция – естественно, будет иметь отрицательное значение (это затрата).
• R – ставка дисконтирования, то есть тот процент, под который инвестор может получить средства для вложений (взять банковский кредит, продать свои акции или использовать внутренние средства).
• WACC – средневзвешенная стоимость капитала (от Weighted Average Cost of Capital) – если применяется сразу несколько источников привлечения денег, то процентная ставка будет представлять среднюю величину, рассчитанную пропорционально.

ВАЖНАЯ ИНФОРМАЦИЯ! Было бы очень просто рассчитать внутреннюю норму доходности, зная все необходимые показатели. Однако на практике невозможно определить точные величины денежных потоков и однозначно вычислить ставку дисконтирования. Поэтому для каждого отдельного проекта оценивают степень зависимости NPV от процентной ставки.

Формула расчета внутренней нормы рентабельности

IRR – это такая величина R, при которой NPV равен нулю. Поэтому этот показатель можно вывести из формулы расчета приведенной суммы денежных потоков.

• 0 означает величину NPV;
• n – количество исследуемых временных периодов;
• CF_t – денежные потоки в учетный момент времени.

Способы вычисления ВНД

Посчитать значение внутренней нормы доходности вручную не представляется возможным, так как, если вывести из него значение IRR, оно получится множителем 4 степени. Вычислить этот показатель можно несколькими способами:

• использовать специальный финансовый калькулятор;
• применить программу Excel, в которой эта функция встроена в раздел «Финансовые формулы» под названием ВСД («внутренняя ставка доходности»);
• воспользоваться одним из онлайн-калькуляторов;
• применить графический способ (использовался до широкого распространения Персональных компьютеров).

Достоинства и недостатки метода IRR

Для оценки инвестиционных возможностей главным образом применяются два метода – вычисление NPV и IRR. Метод определения внутренней нормы доходности относителен, поэтому не может претендовать на высокую точность, однако обладает рядом преимуществ:

• помогает достаточно просто оценить рентабельность инвестиционного проекта;
• показывает максимально допустимый размер затрат для вложения в проект;
• позволяет сравнивать различные проекты по рентабельности, даже если они отличаются по масштабу и протяженности во времени.

Недостатки метода IRR:

• нельзя посчитать абсолютную доходность инвестиции (то есть сколько конкретно денег – рублей, валюты – она может принести инвестору);
• возможно завышение инвестиционного эффекта, если ВНД сильно отличается от уровня реинвестиций компании (то есть положительные денежные потоки «возвращаются» инвестору с процентной ставкой, не совпадающей с ВНД);
• при вычислении имеет место пренебрежение последовательностью денежных потоков (для формулы не важно, в какой последовательности наступают затраты и приходит прибыль, тогда как на практике это может иметь решающее значение);
• возможны искажения при оценке взаимоисключающих инвестиционных проектов.

Интерпретация внутренней нормы доходности

Главное правило, по которому оценивают возможность инвестирования по показателю ВНД: проект можно принять, если IRR выше, чем средневзвешенная стоимость капитала для компании (WACC). Это значит, что инвестору стоит занимать деньги для вложения, и они, вероятнее всего, принесут добавочную прибыль.

НАПРИМЕР. Банк может предоставить инвестору деньги под 12% годовых. Инвестор собирается взять кредит и вложить средства в проект, ВНД которого 16%. Это значит, что 16% годовых – верхняя планка, по которой можно занять деньги для этого проекта. Если проект действительно принесет 16% прибыли, в пользу инвестора останется 4%, в любом случае он сможет вернуть заемные средства без убытка для себя.

Пример применения ВНД

Приведем жизненный пример оценки внутренней доходности, который может осознать обычный гражданин, а не только предприниматель.

Сдача квартиры в аренду – вроде бы выгодное мероприятие. Но все зависит от того, есть ли эта квартира в собственности. Если это так, то первоначальная инвестиция равна нулю, поэтому проект заведомо рентабелен. Но если планируется вложить средства в покупку квартиры, сдавать ее, а затем продать, чтобы вернуть взятый на это кредит?

Посчитаем, получится ли этот проект выгодным. Пусть квартира стоит 5 млн руб., а сумма аренды за год составит 25 000 руб. в месяц. Пренебрежем налоговыми расходами на оформление покупки квартиры и аренды. За 3 года доход от аренды составит 25 000 х 3 = 75 000 руб. Представим, что конъюнктура рынка недвижимости за 3 года не изменилась и квартиру удастся продать за цену покупки. Значит, спустя три года инвестиция принесет доход 75 000 + 5 млн руб. ВНД такого проекта получится равным приблизительно 6%.

Как известно, ставка кредитования в банке приблизительно составляет 9%, значит, имея в своем распоряжении свободные средства (например, получив их в наследство), их выгоднее положить на депозит, чем покупать квартиру с целью аренды.

Но если стоимость квартиры за эти годы существенно увеличится, ВНД проекта также изменится в лучшую сторону.

Источник

Как анализировать внутреннюю норму доходности (IRR)?

У вас есть отличная идея для нового продукта, который увеличит прибыль или новой системы, которая снизит затраты компании. Но как вы можете быть уверены, что эта идея окупит вложенные инвестиции? Один из основных методов выяснить это — анализ IRR.

Каждый раз, когда вы предлагаете капитальные затраты, вы можете быть уверены, что старшие руководители захотят выяснить их рентабельность (ROI).

Разберемся, как работает IRR и в каких случаях его лучше использовать.

Что такое внутренняя норма доходности?

IRR — это ставка, при которой проект достигает уровня безубыточности (т.е. окупает себя).

Обычно этот показатель используется финансовыми аналитиками в сочетании с чистой приведенной стоимостью или NPV. Это связано с тем, что оба метода похожи, но используют разные переменные.

С помощью NPV вы определяете ставку дисконтирования для своей компании, а затем вычисляете текущую стоимость инвестиций с учетом этой ставки (здесь подробнее о NPV).

Но для IRR вы рассчитываете фактический доход по денежными потоками проекта, а затем сравниваете его с барьерной ставкой вашей компании (т.е. с минимальным ожидаемым уровнем доходности вашей компании). Если IRR выше, то инвестиции выгодны.

Как рассчитывается IRR?

Это не простой расчет. Например, предположим, что вы предлагаете инвестиции в размере 3 000 д.e., которые принесут 1 300 д.e. за каждый год из следующих 3 лет. Вы не можете просто использовать общий денежный поток в размере 3 900 д.е (1 300 * 3) для определения нормы доходности, поскольку он распространяется на период, превышающий эти 3 года.

Вместо этого вам придется использовать итеративный процесс, в котором вы будете пытаться использовать разные барьерные ставки (или годовые процентные ставки), пока ваш NPV не будет равен нулю.

Для расчета этого показателя вам необязательно углубляться в математику, — вы можете легко вычислить его в Exсel (функция ВСД или IRR) или на финансовом калькуляторе.

Как компании используют его?

Компании обычно используют как NPV, так и IRR для оценки инвестиций.

NPV говорит вам больше об ожидаемой рентабельности, но при этом финансовые аналитики «часто полагаются на IRR в презентациях для нефинансовых людей».

Это связано с тем, что IRR гораздо более прост и интуитивно понятен.

Когда вы говорите: «Если у меня есть проект, где IRR составляет 14%, а наша корпоративная барьерная ставка составляет 10%», ваша аудитория думает: «О, я понимаю. Мы получаем на 4% больше прибыли от этого проекта».

Если бы вы сказали, что NPV в этом проекте составляет 2 млн. д.е., ваша аудитория весьма вероятно попросит напомнить о том, что такое NPV, и может запутаться, прежде чем вы хотя бы частично объясните значение того, что «текущая стоимость будущих денежных потоков от этих инвестиций с использованием нашей 10% барьерной ставки превышает наши первоначальные инвестиции на 2 миллиона д.е.».

Недостатком этого показателя является то, что IRR гораздо более концептуальна, чем NPV. Используя NPV, вы оцениваете денежный доход компании: если предположить, что все предположения верны, этот проект принесет 2 млн. д.е. IRR не дает вам реальных денежных цифр.

Точно так же IRR не затрагивает вопросы масштаба. Например, IRR 20% не говорит вам ничего о сумме денег, которую вы получите. Это 20% от 1 миллиона д.е.? Или от 1 д.е.? Не обязательно быть математиком, чтобы понять, что между этими цифрами есть большая разница.

Какие ошибки делают люди при использовании IRR?

Самая большая ошибка заключается в том, чтобы использовать исключительно IRR.

Гораздо лучше анализировать проект, используя хотя бы один из других методов — NPV и/или срок окупаемости.

Использование только этого показателя может привести к тому, что вы будете принимать плохие решения о том, куда инвестировать с трудом заработанные деньги вашей компании, особенно при сравнении проектов, имеющих разные сроки.

Скажем, у вас есть годичный проект с IRR 20% и 10-летний проект с IRR 13%. Если вы основываете свое решение только на IRR, вы можете поддержать 20%-ный проект IRR. Но это было бы ошибкой. Вам выгоднее IRR 13% в течение 10 лет, чем 20% в течение одного года, если ваша корпоративная барьерная ставка будет составлять 10% в течение этого периода.

Вы также должны быть осторожны с тем, как IRR учитывает временную стоимость денег. IRR предполагает, что будущие денежные потоки от проекта реинвестируются в IRR, а не в стоимость капитала компании, и поэтому этот показатель не так точно отражает связь с капиталом и временной стоимостью денег, как NPV.

Модифицированная внутренняя норма доходности (MIRR), предполагающая, что положительные денежные потоки реинвестируются в капитал фирмы, более точно отражает стоимость и рентабельность проекта.

Тем не менее, следует всегда использовать IRR в сочетании с NPV, чтобы получить более полную картину того, какую отдачу принесут ваши инвестиции.

Источник

Показатель внутренней нормы доходности и его модификации

Исследованы свойства показателя внутренней нормы доходности инвестиционных проектов. Известно, что этот показатель для многих проектов не существует или определяется неоднозначно. Поэтому имеется много предложений по замене его другими показателями с более широкой областью определения. В настоящей работе рассмотрены такие предложения и показана их некорректность. По работе выпущен препринт.

Предлагается система аксиом, отражающих основные свойства внутренней нормы доходности, и устанавливается структура удовлетворяющих им показателей. Доказано, что, если проекты с одинаковой доходностью остаются таковыми при аффинном преобразовании временной оси, показатель доходности совпадает (с точностью до монотонного гладкого преобразования) с “обычным” показателем внутренней нормы доходности. Рассмотрен также вопрос об определении внутренней нормы доходности применительно к проектам со случайными расходами и доходами.

1. ИНВЕСТИЦИОННЫЕ ПРОЕКТЫ И ВНД

Одним из показателей эффективности инвестиционных проектов является внутренняя норма доходности (ВНД). Однако разные авторы дают этому показателю разные определения и указывают разные сферы применения, а также нередко приписывают ему свойства, которыми он на самом деле не обладает. Более того, поскольку ВНД может быть определена не для любых инвестиционных проектов, в литературе предлагаются различные способы “обойти” эту трудность. В настоящей работе предпринята попытка более глубоко разобраться в этой проблеме, дать корректное определение ВНД и более глубоко исследовать возможности его модификаций.

Авторы приносят благодарность своим коллегам по научной и практической деятельности В.И. Аркину, В.З. Беленькому, В.Н. Лившицу, В.М. Полтеровичу и А.Д. Сластникову, принявшим активное участие в обсуждении рассматриваемых в данной работе проблем и сделавших ценные замечания.

Инвестиционные проекты и их денежные потоки

Объектом нашего рассмотрения будут инвестиционные проекты. Под инвестиционным проектом мы понимаем комплекс действий, направленных на достижение определенных целей и предусматривающий осуществление инвестиций, т.е. затрат, увеличивающих стоимость основного и оборотного капитала. Содержательное описание указанного комплекса действий излагается обычно в проектных материалах . Субъекты, перечисленные в проектных материалах как исполнители соответствующих действий, являются участниками проекта (в их число, помимо частных фирм, может входить и государство). В отличие от других коммерческих и финансовых операций инвестиционные проекты обычно уникальны, неделимы и нетиражируемы .

Эффективность проекта в широком смысле характеризует его соответствие целям и интересам участников. Однако далее этот термин используется в более узком смысле, как синоним экономической (коммерческой или финансовой) эффективности, относящейся только к коммерческим интересам. В любом случае оценка эффективности базируется на связанных с его реализацией денежных потоках (потоках доходов и расходов) и подразумевает определенное разграничение “собственно проекта” и “окружающей среды” Такое разграничение обычно осуществляется двояко.

На ранней стадии проектирования, когда состав участников точно не определен и их действия не конкретизированы, все будущие участники проекта агрегируются в одного, “виртуального” (но иногда и реального) участника. Считается, что все предусмотренные проектом действия будут осуществляться только этим участником и за его счет, и что он же будет получать все выгоды от реализации проекта. Разграничение “проекта” и “окружающей среды” проводится здесь по продуктам (товарам, работам, услугам): одни из них участник приобретает “со стороны”, другие — производит сам и продает “на сторону”. Соответственно возникают потоки расходов и доходов по проекту. Эти потоки определяют в данном случае эффективность “ проекта в целом ”.

На более поздних стадиях проектирования, когда состав участников и их действия конкретизированы, под “окружающей средой” понимается совокупность экономических субъектов, не являющихся участниками проекта, а также совокупность действий участников, не связанных с проектом. В то же время такие операции, как предоставление займов одним участником другому, включаются в состав предусмотренных проектом действий и учитываются при определении доходов и расходов. Теперь денежные потоки определяются для каждого участника, они носят приростной характер (т.е. отражают влияние проекта на затраты и доходы от всей деятельности участника) и являются базой оценки эффективности его участия в проекте . Далее мы будем иметь в виду именно такую эффективность и рассматривать все проекты с точки зрения одного и того же участника (Субъекта), так что денежные потоки и основанная на них оценка инвестиционного проекта будут относиться только к нему. Это не слишком сужает проблему, ибо с формальной точки зрения эффективность проекта в целом есть эффективность участия в нем единственного “виртуального” участника.

Чрезвычайно важно отметить, что говорить об эффективности проекта можно только тогда, когда он реализуем , т.е. когда все предусмотренные им действия выполнимы. Однако, если с “технической” реализуемостью всё ясно, то “финансовая” реализуемость создает определенные проблемы. Грубо говоря, для финансовой реализуемости необходимо, чтобы Субъект в момент осуществления затрат располагал необходимыми для этого денежными средствами.

Источником этих средств не могут быть другие участники проекта, поскольку движение финансовых ресурсов от одного участника к другому уже учтено при определении денежных потоков каждого. Поэтому потребность в денежных средствах может покрываться Субъектом только за счет деятельности, не связанной с проектом (“сторонней”). Наоборот, получаемые при реализации проекта доходы Субъект может направлять на финансирование каких-то других проектов. Таким образом, для оценки реализуемости проекта необходимо иметь дополнительную информацию об “окружающей среде”, а именно — о “сторонней” деятельности Субъекта. При этом проект может считаться финансово реализуемым, если в любой момент расходы по проекту не превышают доходов от “сторонней” деятельности, а доходы — превышают связанные с этой деятельностью расходы. Из-за этого проект, требующий больших расходов, может оказаться финансово реализуемым, а проект, дающий через год большие доходы — финансово нереализуемым. Эти обстоятельства позволяют объяснить, почему крупная фирма с устойчивым финансовым положением отказывается от выгодного во всех отношениях проекта: одной из причин здесь может быть напряженность финансового плана фирмы, исключающей возможность вложения необходимых средств именно в предусмотренное проектом время.

Мы видим, таким образом, что “сторонняя” деятельность Субъекта, не влияя на эффективность оцениваемого проекта, в то же время во многом определяет его финансовую реализуемость. Поэтому, в отличие от оценки эффективности проекта, которая может и должна осуществляться на основе проектных материалов, оценка его финансовой реализуемости требует использования информации об “окружающей среде”. Поскольку нам не хотелось бы выходить за пределы “собственно проекта”, мы будем считать все проекты, о которых пойдет речь ниже, финансово реализуемыми .

Дискретные проекты и операции с ними

Рассмотрим вначале дискретные проекты, по которым доходы и расходы осуществляются в некоторое конечное число моментов времени t1, …, tm . При этом допускается, что в один и тот же момент времени осуществляются расходы и одновременно получаются доходы. Поэтому каждому моменту времени ti мы сопоставляем один показатель — эффект (чистый доход) fi , отражающий разность между суммой полученных и суммой затраченных в этот момент денежных средств (методические проблемы, связанные с практическими расчетами размеров эффекта, освещены в [1]). Эффекты проекта могут быть как положительными, так и отрицательными. В тех случаях, когда это имеет значение, положительный эффект будем именовать доходом , отрицательный — расходом .

Здесь полезно учесть ряд существенных обстоятельств. Прежде всего, в составе расходов учитываются не только текущие, но и капитальные затраты. Однако амортизация ранее приобретенного оборудования, включаемая в себестоимость продукции, в денежных потоках не отражается (с одной стороны, она не является “платежом на сторону”, с другой — затраты на приобретение оборудования нельзя включать в денежные потоки дважды: в составе инвестиций и в составе затрат на производство продукции). Поэтому отрицательный эффект не означает убыточности производства, а положительный — его прибыльности. Наконец, расходы по проекту отражают не только реальные платежи “на сторону”. Например, если инвестор вкладывает в реализацию проекта собственный автомобиль, его стоимость включается в состав затрат. Поэтому отрицательный эффект здесь не сопровождается уменьшением денежных средств на счетах инвестора.

Заметим также, что реальные инвестиционные проекты дискретны, хотя частота осуществления платежей довольно высокая (не менее десятка платежей в сутки). Поэтому на практике соответствующие денежные потоки либо рассматривают как непрерывные (см. п. 3.1), либо агрегируют, условно принимая, например, что все платежи в течение каждого года осуществляются в начале года. Именно так надо рассматривать приводимые ниже примеры, где денежные потоки даны с годовой разбивкой.

Любой дискретный проект F допускает представление совокупностью пар <( t1 , f1 ); … ; ( tm , fm )>. Один и тот же проект может иметь несколько представлений. Мы отождествляем представления, различающиеся порядком пар или добавлением или исключением пар с нулевыми эффектами вида ( ti , 0 ). Проект <( s , 1)>, предусматривающий получение эффекта 1 в момент s , будем обозначать через .

Наиболее ранний и наиболее поздний из моментов получения ненулевых эффектов ti назовем соответственно началом и концом проекта и обозначим a( F ) и z( F ).

Говоря о двух или нескольких инвестиционных проектах, мы по умолчанию будем считать их независимыми . Это означает, что реализация одного проекта не влияет на затраты и доходы по остальным (в динамических моделях неймановского типа аналогичное требование формулируется как “отсутствие внешней экономии или внешней неэкономичности” [2]). Требование независимости необходимо, поскольку решения о реализации зависимых проектов должны приниматься при их совместном рассмотрении, тогда как решения о реализации независимых проектов могут приниматься децентрализованно (каждый из таких проектов может быть принят или отклонен и это не повлияет на решения о реализации остальных). Далее, рассматривая проекты с одинаковыми представлениями, мы считаем, что имеем дело не с одним и тем же проектом, а с несколькими его независимыми “копиями” .

Проекты, по которым моменты t1, …, tm получения эффектов одни и те же, назовем синхронными . Легко видеть, что любые два проекта можно сделать синхронными, добавив к их представлениям необходимое число пар с нулевыми эффектами. В то же время сделать синхронными бесконечное множество проектов можно не всегда.

Некоторые изменения денежных потоков на практике рассматриваются как улучшения проекта в том или ином смысле. Соответствующие отношения между проектами могут быть формализованы с помощью двух отношений предпочтения .

Первое (» ) описывает ситуацию, когда один проект получается путем увеличения всех или некоторых эффектов другого: F = <( t1 , f1 ); … ; ( tm , fm )>» G = <( t1 , g1 ); … ; ( tm , gm )>, если fi > gi для всех i , причем fi > gi хотя бы для одного i . Например, F + » F .

Второе (> ) связано с такими изменениями проекта, когда доходы переносятся на более ранние, а расходы — на более поздние сроки. Это отношение сходно с отношением первого стохастического доминирования для функций распределения вероятностей и может быть определено так:

если для всех Т , причем для какого-либо Т здесь имеет место строгое неравенство. Например, F + — > F при s t .

Операция умножения проекта на число определяется естественным образом:

При положительном k эта операция отражает изменение денежных потоков при изменении масштаба реализации проекта (например, при покупке k машин вместо одной). При k = -1 эта операция заменяет доходы расходами и наоборот. Очень условно она может быть интерпретирована как переход от денежных потоков продавца к денежным потокам покупателя при реализации того же проекта.

Операцию суммирования проектов естественно определить только для синхронных (и, естественно, независимых) проектов:

Эта операция, очевидно, однозначно определена для любых двух проектов, поскольку их всегда можно сделать синхронными. Она отражает изменение денежных потоков при одновременной реализации двух независимых проектов, когда получаемые в одни и те же моменты времени эффекты суммируются. Легко видеть, что .

Проект, у которого наиболее ранний эффект отрицателен, а наиболее поздний эффект положителен (т.е. проект, начинающийся с расходов и завершающийся доходами), будем называть регулярным . Легко видеть, что умножение регулярного проекта на положительное число переводит его в регулярный, и сумма регулярных проектов также будет регулярным проектом.

Далее нам понадобятся “элементарные” регулярные проекты <( r, -K ); ( s , P )>, предусматривающие затраты K в момент r и получение дохода P > 0 в момент s > r . Мы будем называть их депозитами и обозначать . Если речь идет об “обычном” депозите с непрерывным начислением процентов (так начисляются проценты по счетам в Сбербанке РФ) по ставке 100s%, то доход по нему определяется формулой . На этом основании определим ставку депозита как величину . Такая ставка может быть и отрицательной. Это будет, например, когда проценты по депозиту начисляются по положительной ставке, меньшей, чем темп инфляции: тогда размер возврата депозита в реальном исчислении будет меньше размера самого депозита. Та же ситуация может возникнуть, если проект “физически” не является депонированием, а состоит, скажем, в приобретении и последующей продаже ценных бумаг в условиях падающей их курсовой стоимости. Особо выделим депозиты вида <( r, -K ); ( s , K )>с нулевой ставкой . Они отвечают проектам, предусматривающим “простое хранение” финансовых ресурсов и мы будем именовать их тезаврациями . Отметим также, что любой депозит является результатом умножения депозита вида на положительное число.

Пусть l( t ) — непрерывная возрастающая функция от t , l(- ¥ ) = — ¥ , l( ¥ ) = ¥ . Тогда преобразование оси времени в себя L: t ® l( t ) гомеоморфно и переводит проект F = <( t1 , f1 ); … ; ( tm , fm )>в проект L F =<(l( t1 ), f1 ); … ; (l( tm ) , fm )>. Частным случаем таких преобразований является тождественное I : t ® t и аффинное ( изменение шкалы времени ) : t ® q t+ t (q > 0). Последнее отражает изменение денежного потока в ситуации, когда переносится на t начало реализации проекта (c соответствующим сдвигом всех остальных моментов получения эффектов) и одновременно в q раз меняется интенсивность выполнения предусмотренных проектом действий.

Реальные инвестиционные проекты также предусматривают дискретное осуществление расходов и получение доходов. Другое дело, что эта дискретность наиболее существенна по отношению к финансовым проектам (получение и предоставление кредитов, операции с ценными бумагами). По “обычным” проектам, предусматривающим инвестиции в производство, платежные операции производятся несколько раз в день. В расчетах эффективности таких проектов соответствующие денежные потоки либо рассматриваются как “непрерывные” (эту ситуацию мы рассмотрим позднее), либо агрегируются. В последнем случае условно принимается, что все платежи в течение каждого месяца, квартала или года осуществляются в один и тот же момент времени (например, в начале соответствующего периода).

Интегральный эффект и внутренняя норма доходности проекта

Основным показателем эффективности проекта является интегральный дисконтированный эффект (ИДЭ), чистый дисконтированный доход (ЧДД), Net Present Value (NPV). Для дискретного проекта F = <( t1 , f1 ); … ; ( tm , fm )>он определяется формулой

. (1)

Входящий сюда показатель r называется (непрерывной) нормой дисконта (discount rate), необходимой нормой доходности или прибыли (RRR) и отражает, с одной стороны, межвременные предпочтения Субъекта, осуществляющего расходы и получающего доходы по проекту, а с другой — доходность альтернативных и доступных для Субъекта направлений инвестирования. Мы не будем рассматривать проблемы, связанные с установлением таких норм, а также с учетом влияния инфляции на эффективность проектов, предполагая, что либо инфляция отсутствует, либо все эффекты исчислены в дефлированных ценах. Если поведение Субъекта экономически рационально и его норма дисконта равна r, то проекты с неотрицательным V (r; F ) он должен оценивать как эффективные и принимать к реализации, а проекты с отрицательным V (r; F ) — оценивать как неэффективные и отвергать.

Приведем одно из возможных объяснений экономического смысла критерия ИДЭ. В общем случае экономическая эффективность проекта отражает последствия его взаимодействия с “окружающей экономической средой”. При этом “собственно проект” определяет размеры потребляемых и производимых продуктов, а “внешняя среда” — стоимостные оценки этих продуктов. Эти оценки принимаются в расчетах исходя из цен, сложившихся на рынке, и их прогноза (вероятностный характер прогнозируемых цен может быть учтен при рассмотрении эффектов проекта как случайных величин; этот аспект частично рассматривается в разд. 6 и более подробно — в [3]). При этом, разумеется, учитывается, что один и тот же товар, продаваемый сегодня разными продавцами на разных условиях, может иметь разную цену. Поэтому в общем случае цены продуктов, закладываемые в расчет, не обязаны совпадать ни со среднерыночными, ни с ценами конкретного продавца. Обратим внимание теперь, что единица продукта сегодня и та же единица через год являются разными экономическими благами (см., напр. [4, с. 34-35, 255]). Эта неравноценность отражается рыночной категорией “стоимость капитала” и отражается в различных показателях, таких как кредитные и депозитные процентные ставки, доходность государственных ценных бумаг или цены фьючерсных сделок. Норма дисконта является при этом той “стоимостью капитала”, которую Субъект считает необходимым заложить в расчет эффективности конкретного проекта, и является важной характеристикой “окружающей среды”.

Однако на стадии разработки проекта (особенно, если она выполняется не самим Субъектом, а по его поручению) норма дисконта может быть точно не известна. Более того, предпочтения Субъекта могут измениться после того, как проект будет разработан. В этой связи в ходе разработки проекта выясняют, как меняется интегральный дисконтированный эффект при изменении нормы дисконта r в некотором “разумном” диапазоне. При этом возникает следующая важная характеристика эффективности проекта — внутренняя норма доходности (ВНД, внутренняя норма рентабельности, прибыли или эффективности, Internal Rate of Return, IRR).

Формально ВНД проекта F определяется как такое значение R ( F ) нормы дисконта, при котором ИДЭ обращается в нуль, т.е. как корень уравнения доходности

Поскольку для некоторых проектов это уравнение может вообще не иметь решения, показатель ВНД определен не для всех проектов,. К тому же данное формальное определение требует дополнений, ибо неясно, какой из корней принимать в качестве ВНД, если этих корней несколько. Для того, чтобы дать корректное определение ВНД, введем вначале удобную классификацию корней уравнений типа (2) и рассмотрим класс “типичных” проектов, для которых установление ВНД никаких сложностей не представляет.

Если при переходе через корень функция V ( x ) меняет свой знак с положительного на отрицательный, такой корень будем называть нормальным , в противном случае — аномальным . В свою очередь, нормальные корни функция f ( x ) разделим на строго нормальные, в которых производная V ¢ ( x ) отрицательна, и нестрого нормальные , в которых эта производная равна 0.

“Типичный” проект F = <( t1, f1 ); … ; ( tm, fm )>характеризуется тем, что в нем расходы осуществляются до получения доходов: fi > 0 > fj Þ ti > tj. Для таких проектов, как легко проверить, функция V ( x ; F ) устроена следующим образом: она имеет единственный корень R , положительна при x и отрицательна при x > R . Поэтому для оценки эффективности такого проекта внутреннюю норму доходности R ( F ) сравнивают с нормой дисконта Субъекта: проект оценивается как эффективный, если ВНД не меньше нормы дисконта и как неэффективный в противном случае.

Учитывая указанное обстоятельство, представляется естественным определять ВНД в общем случае следующим способом. Проект F называется допустимым , если функция V ( x ; F ) положительна при больших отрицательных x, отрицательна при больших положительных x и имеет единственный корень, к тому же нормальный. Этот корень R ( F ) и является (непрерывной) внутренней нормой доходности допустимого проекта.

Однако, несмотря на всю “естественность”, такое определение не очень удачно. Дело в том, что корень функции V ( x ; F ) может быть нестрого нормальным. Казалось бы, в этом ничего плохого нет. Однако при этом небольшое изменение проекта может привести (но может и не привести) к “размножению” корней — например, вместо одного корня могут возникнуть три. При этом ВНД “исчезает” и потому не может рассматриваться как непрерывная функция от параметров проекта. Учитывая, что подобное явление может свидетельствовать о неустойчивости проекта, мы исключим подобные ситуации из рассмотрения. Таким образом, проект F называется допустимым, если и только если функция V ( x ; F ) имеет единственный строго нормальный корень R ( F ), который и считается ВНД проекта F . Допустимый проект мы рассматриваем как эффективный, если и только если его ВНД не меньше нормы дисконта r для Субъекта.

Величина называется чистым доходом (ЧД) — Net Value (NV) — проекта. Она также используется при оценках эффективности: проекты с отрицательным ЧД при этом обычно рассматриваются как неэффективные. Это согласуется и с определением ВНД, поскольку отрицательность ЧД для допустимого проекта означает, что его ВНД отрицательна и, стало быть, меньше нормы дисконта.

Условия допустимости проекта трудно выразить в виде каких-то простых ограничений на значения его эффектов. Вместе с тем, проект будет недопустимым, если его ИДЭ будет положителен при больших положительных нормах дисконта или отрицателен при больших отрицательных нормах дисконта. Отсюда следует, что недопустимыми будут проекты, начинающиеся с доходов или кончающиеся расходами. Таким образом, регулярность дискретного проекта есть необходимое условие его допустимости. Однако одной регулярности недостаточно. Так, из тождества

видно, что проект регулярен, но недопустим: V ( x ; K ) имеет корни x = 0, ln2 и -ln2. При этом x = 0 является аномальным корнем, т.е. V ¢ (0; K ) > 0.

На практике обычно используют не непрерывную , а годовую норму дисконта Е. Соответственно дисконтирование разновременных эффектов производится путем умножения их не на , а на . Приравнивание так исчисленного ИДЭ к нулю (при прочих аналогичных условиях) позволяет определить “годовую” ВНД. Если непрерывная и годовая ВНД близки к нулю (что обычно бывает в реальных проектах), они мало отличаются друг от друга. Нижним пределом непрерывной ВНД является, очевидно, — ¥ , тогда как нижним пределом годовой ВНД является -1. Рискуя навлечь на себя гнев традиционных экономистов, мы, тем не менее, будем далее оперировать с непрерывными нормами дисконта и ВНД, опуская к тому же термин “непрерывная”.

Трактовка ВНД как измерителя доходности проекта связана со следующим обстоятельством. Рассмотрим проект, требующий расходов (вложений) C в некотором году t и обеспечивающий доход C (1+ R ) в следующем году t +1. Нетрудно убедиться, что этот проект имеет “годовую” ВНД = R . Таким образом, “годовая” ВНД данного проекта отражает тот доход на вложенный капитал, который обеспечивает проект “после того, как окупятся первоначальные затраты”. Трактовка непрерывной ВНД немного сложнее. Рассмотрим проект, предусматривающий депонирование суммы 1 в момент t под 100s % годовых при условии непрерывного начисления процентов и обеспечивающий доход в момент t+ d. Легко проверить, что (непрерывная) ВНД этого проекта, как корень уравнения , равна (непрерывной) ставке депозита и является возрастающей функцией от q (в частности, ВНД тезаврации равна нулю). Более того, проект, состоящий во вложении средств на банковский депозит с непрерывным начислением процентов по ставке s при произвольном графике снятия средств с депозита и/или пополнения депозита, имеет ВНД, равную ставке депозита s.

Основное свойство ВНД, обусловливающее возможность использования этого показателя для оценки эффективности проекта, состоит в том, что ИДЭ проекта положителен при любой норме дисконта, меньшей ВНД, и отрицателен при любой норме дисконта, превышающей ВНД . Наряду с этим, показатель ВНД имеет и ряд других важных свойств.

Монотонность . Если проекты F и G допустимы и F » G , то R ( F ) > R ( G ).

Инвариантность при изменении масштаба . При изменении масштаба проекта он остается допустимым и его ВНД не меняется: R ( F ) = R ( kF ) при k >0. Это свойство часто используется, когда желательно информировать кого-либо об эффективности проекта, не раскрывая его масштабов.

Однородность при изменении шкалы времени . При преобразовании допустимый проект остается допустимым и его ВНД уменьшается в q раз: R ( F ) = q -1 R ( F ).

Инвариантность к одновременной реализации . Если проекты F и G допустимы и имеют одинаковую ВНД, то их одновременная реализация тоже допустима и имеет ту же ВНД:

.

Усредняемость . Если проекты F , G и F + G допустимы и ВНД у проекта F меньше, чем у G , то ВНД проекта F + G больше, чем у F и меньше, чем у G :

Два последних свойства представляются особо важными. Они не позволяют “улучшить” проект, реализовав его совместно с менее доходным и “испортить” хороший проект, реализовав его совместно с еще более доходным. Поэтому, если инвестор отобрал независимые проекты, ВНД которых лежит в некотором интервале, он может быть уверен, что при их совместной реализации будет обеспечена ВНД, лежащая в том же интервале (в частности, если для реализации отобраны проекты с ВНД > 0,2, то при их совместной реализации не может оказаться ВНД 0,1). Это позволяет децентрализовать принятие решений о независимых проектах, и любое подразделение фирмы, приняв проект с высокой ВНД или отклонив проект с низкой ВНД, будет действовать в интересах фирмы в целом (о важности подобных условий, обеспечивающих возможность децентрализованных оценок эффективности проектов, см. в [3, 5, 6]). Таким образом, рассматриваемые аксиомы гарантируют, что, отобрав любую совокупность независимых проектов с ВНД, превышающей норму дисконта, Субъект может быть уверен, что их совместная реализация будет эффективной. Наоборот, отказавшись от реализации какой-то совокупности проектов с ВНД, меньшей нормы дисконта, Субъект может быть уверен в том, что их совместная реализация оказалась бы для него неэффективной. В то же время из свойства усредняемости не следует, что суммирование допустимых проектов с разными ВНД приводит к допустимому — на самом деле такая сумма может оказаться недопустимым проектом.

Особо следует остановиться на свойствах непрерывности ВНД. Прежде всего, дискретный проект характеризуется двумя типами параметров — величинами эффектов и моментами их получения. По отношению к последним показатель ВНД, очевидно, является непрерывной и гладкой (имеющей непрерывную производную) функцией: если проект F = <( t1 , f1 ); … ; ( tm, fm )>допустим, то проекты <( s1 , f1 ); … ; ( sm , fm )>с близкими моментами получения эффектов тоже допустимы и их ВНД близка к ВНД проекта F . Это свойство удобно представить в несколько иной форме:

Непрерывность по времени . Пусть L: t ® l( t ) — непрерывное взаимно-однозначное отображение оси времени на себя. Тогда R (L F ) ® R ( F ), если L ® I , т.е. если l( t ) ® t в равномерной метрике.

В то же время зависимость ВНД от эффектов устроена более сложно. Дело в том, что любой регулярный проект всегда можно “испортить”, предусмотрев получение малых положительных доходов до его начала и осуществление малых расходов (“на ликвидацию предприятия”) после его окончания. При этом проект станет нерегулярным и ВНД перестанет существовать. Поэтому понятие непрерывности ВНД в общем случае требует нетривиального определения. Заметим для этого, что “испорченный” указанным выше способом проект стал нерегулярным потому, что “добавленные” денежные потоки изменили “срок жизни” проекта. Оказывается, что это существенно. Чтобы в этом разобраться, заметим, что изменение величины fi на e hi означает суммирование проекта F с проектом e H = <( ti , e hi )>. Как мы видели, такое суммирование может превратить допустимый проект в недопустимый, если ti F ) или ti > z( F ). Во всех остальных случаях при достаточно малых e проект F останется допустимым, а его ВНД изменится мало. В этой связи удобно ввести следующее определение:

Скажем, что проект G вложен в проект F ( G Í F ), если a( F ) a( G ) z( G ) z( F ).

Тогда, если проект F допустим, а проект Н , не обязательно регулярный, вложен в F , то при e, малых абсолютной величине, будет допустимым и проект F +e H . Это позволяет говорить о непрерывности ВНД в следующем смысле.

Непрерывность по эффектам . Если проект F = <( t1 , f1 ); … ; ( tm, fm )>допустим, а проект H (не обязательно регулярный) вложен в F , то при достаточно малых e проект F + e H будет допустимым и его ВНД будет непрерывной и гладкой функцией от e и hi .

Показатель ВНД имеет довольно широкое (и, по нашему мнению, чрезмерно широкое) практическое применение, что можно объяснить следующим образом. Решения о принятии или отклонении инвестиционных проектов принимают обычно те или иные коммерческие структуры (фирмы, банки, фонды и т.п.), располагающие собственными средствами. Сложилось так, что основная масса инвестиций осуществляется сейчас не в сфере реальных, а в сфере финансовых инвестиций, т.е. в форме операций с ценными бумагами. Денежные потоки по таким проектам устроены довольно просто: вначале осуществляются расходы по приобретению ценной бумаги, затем получаются дивиденды (или купонные выплаты) и, возможно, доходы от продажи ценной бумаги или от ее погашения. Для таких проектов ВНД всегда существует и обычно трактуется как доходность ценной бумаги. Естественно, что коммерческая структура хотела бы использовать тот же показатель и применительно к реальным инвестициям, сохранив, по возможности, его смысл и назначение. К сожалению, в полной мере эту идею реализовать не удается, но поползновения в эту сторону продолжаются.

Отметим ряд распространенных ошибок, связанные с применением ВНД.

1. Если Субъект располагает определенными средствами и может вложить их в несколько проектов из имеющегося портфеля, возникает задача оптимального выбора таких проектов. Оптимальным будет сочетание проектов, обеспечивающее Субъекту (при его норме дисконта) максимальное значение ИДЭ. Между тем, в ряде случаев отбор проектов производят в порядке убывания ВНД (до тех пор, пока хватает средств), что может привести к неверным решениям. Приведем пример.

Будем рассматривать только проекты, требующие единовременных инвестиций К и дающие после этого постоянный ежегодный доход Д . Такие проекты имеют постоянную годовую доходность , она равна Д / К и совпадает с (годовой) ВНД.

Предположим, что некий инвестор, использующий норму дисконта Е = 15 %, превышающую ставку банковского депозита, сравнивает любые варианты таких проектов по критерию ВНД. Пусть сегодня он выбирает между альтернативными (и более выгодными, чем депонирование) проектами 1 и 2, у которых соответственно

К 1 = 2000, Д 1 = 600, ВНД 1 = 0,30;

К 2 = 3000, Д 2 = 840, ВНД 2 = 0,28.

Естественно, такой инвестор выберет проект 1.

Завтра инвестору предлагается другая пара альтернативных проектов, у которых:

К 3 = 3000, Д 3 = 570, ВНД 3 = 0,19;

К 4 = 2000, Д 4 = 360, ВНД 4 = 0,18.

Естественно, такой инвестор выберет проект 3. В результате (пренебрегая разницей в 1 день) он будет иметь годовой доход в размере 600 + 570 = 1170. Если бы он не принял во внимание полученные рекомендации, а поступил, как в известном анекдоте, наоборот, то, затратив на инвестиции ту же сумму (5000), он имел бы более высокий годовой доход 840 + 360 = 1200. Такова цена некоторых рекомендаций.

Отметим, что, казалось бы, явно нерациональный принцип ранжирования предлагается для инвестиционных проектов не “с потолка”: он вполне оправдан именно для финансовых проектов, где, выявив ценную бумагу с наибольшей доходностью, можно обычно приобрести максимально возможное количество таких бумаг, а, если останутся средства, перейти к приобретению ценных бумаг со следующей по величине доходностью. Несоответствие критериев возникло здесь потому, что в отличие от инвестиционных проектов финансовые проекты обычно тиражируемы и делимы, тогда как инвестиционные — уникальны (в инвестиционном портфеле может оказаться несколько “копий” одного и того же проекта, но это скорее исключение, чем правило).

О другой причине применения ВНД для ранжирования проектов подробно говорит П. Массе [4], упоминая при этом Бём-Баверка, Ф. Хайека и других авторов, использовавших подобный критерий. При этом норма дисконта (у П. Массе — процентная ставка), отражающая равновесную цену при обмене “1 франка в настоящий момент” на “1 франк через год”, рассматривается им как “экономический фильтр”: “Если процентная ставка известна, то критерий максимума дисконтированной суммарной прибыли позволяет решить … проблему выбора капиталовложений. В этом случае критерий максимума нормы эффективности (ВНД — авт.) представляется излишним. Однако может случиться, что как раз в силу несовершенства денежного рынка нельзя будет придти к общему соглашению относительно величины нормы дисконтирования. В таком случае норма эффективности вложений может сыграть полезную роль, так как интуитивно ясно, что она является по крайней мере качественным показателем значения операции инвестирования, поскольку чем выше эта норма, тем лучше позволяет такая операция возместить вложенный капитал. Даже с первого взгляда видно, что упорядочение вложений по норме их эффективности имеет то преимущество, что не требует никаких предположений относительно настоящих и будущих значений процентной ставки. Тем самым этот способ позволяет устранить одно из самых серьезных препятствий на пути применения метода дисконтирования, используя характеристику, внутренне присущую капиталовложению, — причина, по которой ряд авторов называет этот параметр внутренней нормой эффективности капиталовложений. Однако если хорошо подумать, ясно, что подобная легкость решения проблемы отражает лишь стремление обойти ее. Получаемый при этих условиях (максимизируя норму эффективности капиталовложения) оптимум будет зависеть от совокупности цен на производительные факторы и продукты, исключая при этом самую существенную для этой области экономических явлений цену — процентную ставку. Тот же самый результат мы получим и при процентной ставке, равной 3 % и при процентной ставке в 12 %, т.е. мы получим одинаковое решение для глубоко различных ситуаций на рынке капиталов. Такое положение представляется неприемлемым” [4, стр. 47-48].

2. Считается, что большое превышение ВНД над нормой дисконта свидетельствует об устойчивости проекта к небольшим изменениям доходов и расходов. Следующий пример показывает, что это не всегда так.

Проект предусматривает инвестиции 4900 в году 0 и обеспечивает получение доходов в последующие 4 года в размерах соответственно 1950, 1790, 1610, 1520. Для его финансирования используются собственные средства (500) и кредит в объеме 4400, предоставляемый под 14 % годовых сроком на 4 года. Таким образом, в первые 4 года возникают дополнительные расходы на погашение кредита (по 1100) и на уплату процентов (соответственно 616, 462, 308 и 154). При этом движение собственных денежных средств фирмы характеризуется денежным потоком, описанным в табл. 1.

1950-1100- -616 = +234

1790-1100- — 462 = +228

1610-1100- — 308 = +202

1520-1100- -154 = +266

Нетрудно проверить, что такой проект имеет ВНД = 30,0 % и эффективен при норме дисконта Е = 10 %. Казалось бы, при столь большом превышении ВНД над нормой дисконта проект должен быть устойчив, о чем прямо говорится в [7, стр. 119]. Рассмотрим, однако, ситуацию, когда в процессе реализации проекта возникают непредвиденные инвестиции в не слишком большом размере 250 (5,1 %). Легко проверяется, что при этом денежный поток года 0 уменьшается на 250, проект становится неэффективным, а его ВНД становится равной 9,1 %. Таким образом, высокая ВНД не гарантирует устойчивости проекта !

3. Считается, что при наличии у V ( x ; F ) нескольких корней иногда можно принять в качестве ВНД один из них. Однако при этом может не обеспечиваться непрерывность, монотонность или иные свойства ВНД (другие обоснования даны в разд.3). Действительно, для регулярных проектов функция V ( x ; F ) положительна при больших отрицательных x и отрицательна при больших положительных x . Поэтому отсутствие ВНД обычно означает, что V ( x ; F ) имеет три корня, из которых наибольший и наименьший — нормальные, а средний — аномальный. Какой бы из них ни принять в качестве ВНД, ИДЭ проекта не будет сохранять знак либо справа, либо слева от этого корня, что не позволяет оценить эффективность проекта путем сравнения ВНД с нормой дисконта. Кроме того, если принимать за ВНД меньший корень, то можно так улучшать проект, чтобы этот корень сближался со средним и в конце концов исчез — при этом проект станет допустимым, а его ВНД скачком увеличится. Аналогичный скачок можно “организовать”, если в качестве ВНД брать больший корень. Если же в качестве ВНД брать средний корень, то легко привести примеры, когда он растет при ухудшении проекта и снижается при его улучшении.

В этой связи квалифицированные специалисты считают, что в случае множественности корней ни один из них не может использоваться для характеристики эффективности проекта: “Если проявляется феномен множественных норм прибыли, то ни одна из них не имеет экономического смысла и, следовательно, необходимо использовать другой метод анализа” [8, с. 360].

4. Считается, что ВНД, якобы, является той максимальной процентной ставкой, под которую можно брать кредиты. На самом деле это утверждение верно лишь при выполнении следующих условий:

весь проект осуществляется только за счет займов (поэтому ВНД не может определяться для проекта “в целом”, ибо здесь с самого начала принимается, что проект финансируется полностью за счет собственных средств Субъекта);

кредит, необходимый для реализации проекта, может предоставляться несколькими траншами и погашаться в любое время до прекращения проекта;

избыточные (после расчетов по кредиту) доходы от реализации проекта, если они возникают на каком-то шаге, депонируются (причем ставка депозита совпадает с ВНД) и могут быть использованы для финансирования проекта на следующих шагах;

изменение размеров получаемых кредитов и вложений на депозиты не влияет на суммы уплачиваемых налогов. Это условие предполагает аддитивность налоговой системы. Если оно выполняется, налог по проекту “с кредитами и депозитами” можно “разложить” на часть, относящуюся к проекту “без кредитов и депозитов”, и другую часть, относящуюся только к кредитным и депозитным операциям.

Ясно, что эти условия в большинстве случаев не столь реалистичны, чтобы практически использовать ВНД как критерий допустимой кредитной ставки. Если же уравнение доходности имеет несколько корней, то при выполнении указанных условий проект может быть реализован при использовании заемных средств под ставку, совпадающую с любым из этих корней. Поэтому, если трактовать ВНД как максимальную процентную ставку, то ее надо определять как наибольший из корней уравнения доходности (даже, если он аномальный). Однако при этом нельзя утверждать, что проект будет финансово реализуем при меньшей процентной ставке.

Наконец, важно иметь в виду, что изменение условий финансирования (хотя бы в части размеров и ставок кредита) трактуется нами как изменение всего проекта. Это обусловлено, прежде всего тем, что изменение этих условий меняет денежные потоки Субъекта и, следовательно, эффективность его участия в проекте. Задача расчета максимальной процентной ставки, приемлемой для Субъекта, разумеется, актуальна, однако для ее решения надо построить варианты реализации проекта с разными процентными ставками и отобрать из них те, которые будут финансово реализуемыми для Субъекта и одновременно эффективными для всех остальных участников. Решением будет тот из оставшихся вариантов, который отвечает максимальной процентной ставке и при этом обеспечивает Субъекту неотрицательный ЧДД. Очевидно, что денежные потоки по этому варианту будут весьма далеки от потоков исходного проекта.

5. Оценивая эффективность проекта (особенно с “непрерывным” денежным потоком), нередко пытаются обеспечить “запас эффективности”, принимая моменты осуществления затрат более ранними, а моменты получения доходов — более поздними (т.е. “сдвигая” затраты назад, а доходы — вперед). Считается, что такая операция уменьшает ВНД, т.е. что . На самом деле это неверно. Так, проект G = <(0, -4); (2, 1)>имеет ВНД = -ln2 » -0,69. Перенеся получение дохода 1 на более ранний момент 1, мы получим проект F = <(0, -4); (1, 1)> с меньшей ВНД = -ln4 » -1,38. Можно доказать, что указанные сдвиги моментов получения эффекта уменьшают только положительную ВНД, отрицательные же ВНД при этом будут увеличиваться.

6. Нередко допустимый проект представляют себе как сумму “элементарных” проектов — депозитов с той же доходностью. Это также неверно. Так, проект <(1, -1); (2, 2); (3, -4); (4, 3)>, предусматривающий расходы 1 и 4 в первом и третьем годах и доходы 2 и 3 во втором и четвертом годах, допустим и имеет доходность 0. Легко проверить, что его нельзя представить суммой депозитов с нулевой ставкой (тезавраций).

Многих экономистов печалит, что ВНД определена не для всех проектов. Так, у проектов с большими инвестициями при эксплуатации или ликвидации созданных по проекту предприятий, ВНД не существует. В этой связи все, кому не лень, дают и усиленно рекламируют другие “более приемлемые” показатели, которые, по мнению авторов, способны заменить ВНД при анализе инвестиционных проектов. В настоящей работе сделана попытка рассмотреть и оценить подобные предложения и выяснить, не существует ли иных, кроме ВНД, показателей с примерно теми же свойствами.

В этой связи работа имеет следующую структуру. В п. 2 анализируется ряд предложений по модификации ВНД и отмечаются их весьма существенные недостатки, не позволяющие рекомендовать их для практического применения. Поиск разумной альтернативы ВНД, по нашему мнению, возможен на основе аксиоматического подхода, исходя из требований к допустимым проектам и показателям их доходности, обеспечивающим рациональное экономическое поведение субъектов. Этому посвящен п. 3, где класс дискретных проектов существенно расширяется, формулируются основные аксиомы, которым должен удовлетворять искомый показатель доходности и устанавливается этого показателя. В п. 4 система аксиом пополняется новой аксиомой, описывающей изменения доходности при преобразованиях оси времени, и показывается, что такой системе аксиом удовлетворяет, по существу, только “обычный” показатель ВНД. Таким образом, оказывается, что разумной альтернативы ВНД нет. В то же время в практически важных случаях круг допустимых проектов может быть несколько расширен — некоторые соображения по этому поводу излагаются в п.5. В заключительном п.6 рассматривается вопрос об определении ВНД применительно к проекту со случайными эффектами.

Источник