Talkin go money
Что такое омегаверс? (Июнь 2021).
Table of Contents:
Мы часто слышим термины «альфа» и «бета», когда говорим об инвестициях. Оба эти числа — это цифры, которые измеряют связанные, но разные вещи.
Alpha
Alpha — это число, присвоенное возврату по данному индексу. Так что если вы инвестируете в акции, и он возвращается на 20%, а S & P 500 заработал 5%, то у вас есть альфа 15. 15. -15 означает, что ваши инвестиции отстают на 20%. Альфа также является мерой риска. В приведенном выше примере -15 означает, что инвестиции были слишком рискованными с учетом возвращения. Альфа нуля — это «правильно» — заработал доход, соизмеримый с риском. Альфа больше нуля означает выигрыш в капитале. (Подробнее см. Ниже: Улучшение вашего портфолио с помощью альфа и бета-версии .)
Когда менеджеры хедж-фондов говорят о высокой альфе, они обычно говорят, что их менеджеры достаточно хороши, чтобы превзойти рынок. Но возникает еще один важный вопрос: если альфа — это «избыточное» возвращение над индексом, точно, какой индекс вы используете? Например, менеджер фонда может сказать, что он или она получил 20-процентный доход, когда S & P принес 15%, альфа 5. Но был ли S & P подходящим индексом для использования? Рассмотрим менеджера, который положил все деньги клиента в Apple Inc. (AAPL AAPLApple Inc174. 25 + 1. 01% Создано с помощью Highstock 4. 2. 6 ) акций 1 августа 2014 года По сравнению с S & P 500 альфа выглядела бы неплохо: Apple вернулась 18. 14%, а S & P 500 вернулась 6. 13%, для альфы около 12.
Но маловероятно, что большинство экспертов рассмотрят S & P надлежащее сравнение для Apple, само по себе, учитывая разные уровни риска. Возможно, NASDAQ будет более подходящей мерой. NASDAQ в том же годовом периоде вернул 15. 51%, что подталкивает альфу этих инвестиций Apple вниз 2. 63. Поэтому, судя по тому, имеет ли портфель высокую альфа-версию или нет, полезно спросить, что такое базовый портфель. (Подробнее см. Добавление альфы без добавления риска .)
Это относится к бета-версии. В отличие от альфы, которая измеряет относительную отдачу, бета является мерой относительной волатильности. Если вы поместите все свои деньги во все возможные инвестиции, то ваша бета-версия будет 1. Технический запас в этом случае будет иметь бету выше 1 (и, вероятно, довольно высокую), тогда как T-bill будет близок к нулю, потому что их цены вряд ли двигаться относительно рынка в целом.
Бета — коэффициент умножения. Акции с бета-версией 2 по отношению к S & P 500 увеличиваются или уменьшаются в два раза по сравнению с индексом за данный период времени. Если бета равна -2, то акции перемещаются в противоположном направлении от индекса, в два раза. Некоторые инвестиции с отрицательными бетами являются обратными биржевыми фондами (ETF) или некоторыми типами облигаций. (Подробнее см. Ниже: Бета: знай риск .)
Что бета также говорит вам о том, что вы не можете избавиться от диверсификации.Если вы посмотрите на бета-версию типичного взаимного фонда, это, по сути, говорит вам, сколько риска вы добавляете к портфелю средств.
Повторяются аналогичные предостережения для альфы: важно знать, что вы используете в качестве своего критерия волатильности. Morningstar, Inc. (MORN MORNMorningstar Inc87 58 + 0,55% Создано с Highstock 4. 2. 6 ), например, использует U. S. Treasuries в качестве эталона для бета-расчетов. Фирма берет на себя возврат фонда по ГКО и сравнивает это с возвратом по рынкам в целом, и с использованием этих двух чисел появляется бета-версия. Тем не менее, существует ряд других критериев, которые можно было бы использовать. (Подробнее см. Ниже: Бета: колебания ценовых флуктуаций .)
Нижняя линия
Альфа и бета — это оба коэффициента риска, которые инвесторы используют в качестве инструмента для расчета, сравнения и прогнозирования доходности. Они очень важны, чтобы знать, но нужно тщательно проверить, как они рассчитываются. (Более подробно см .: Более глубокий взгляд на альфа .)
Источник
Коэффициенты бета и альфа
Одним из популярных методов оценки рыночного риска является расчет и анализ показателя систематического рыночного риска – коэффициента бета (Д, beta), оценивающего чувствительность риска акции по отношению к риску всего рынка в целом :
Этот метод основан на модели оценки капитальных активов Шарпа (Capital Asset Pricing Model – CAPM) и применяется для оценки риска акций, котирующихся на фондовых биржах. Поскольку рыночная доходность в общем случае неизвестна, для ее оценки используют какой-либо индекс с широкой базой. Все ценные бумаги, обращающиеся на данном рынке, рассматриваются как «рыночный портфель», а изменение значения наиболее представительного фондового индекса выступает показателем изменений стоимости рыночного портфеля.
Широкое применение индексной модели на практике объяснено тем, что коэффициент бета данной ценной бумаги оценивается за некоторый период времени в прошлом и становится инструментом прогнозирования. Он интерпретируется как мера чувствительности, которая показывает, насколько при заданных или ожидаемых изменениях доходности фондового индекса изменится ожидаемое значение доходности рассматриваемой ценной бумаги.
Одним из косвенных показателей риска служит величина премии за риск – разность доходности данного актива ri , которому присущ риск, и доходности безрисковых вложений rf, в качестве которого на практике часто принимают уровень доходности по казначейским обязательствам США (ri – rf).
Модель САРМ предполагает , что премия за систематический риск данной ценной бумаги пропорциональна премии за риск по рыночному портфелю (индексу) с коэффициентом пропорциональности βi:
В реальности премии за риск конкретных активов могут отклоняться от расчетных премий за систематический риск этих активов, и величина этих отклонений может быть охарактеризована как несистематический (специфический) риск активов, который описывается коэффициентом альфа (α, alpha), показывающим переоценку или недооценку рынком систематического риска для данного актива:
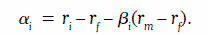
На практике производят статистическое уточнение оценок коэффициентов бета и альфа с учетом различных моделей регрессионной зависимости.
Существуют различные точки зрения на применимость коэффициентов альфа и бета в фундаментальном анализе, в котором положительные или отрицательные значения коэффициента альфа непосредственно интерпретируются как сигналы на продажу или покупку переоцененных (соответственно недооцененных) акций.
Источник
Модели оценки доходности активов
Лекция 20. Модели оценки доходности активов
 |
| |
Инвесторы сталкиваются с проблемой оценки стоимости активов. Она зависит главным образом от их риска и доходности. На рынке выдерживается закономерность: чем выше потенциальный риск, тем выше должна быть и ожидаемая доходность.
Как известно, стоимость актива определяется путем дисконтирования будущих ожидаемых доходов, которые он принесет, под процентную ставку, соответствующую его риску. Модель оценки стоимости активов не дает непосредственного ответа на вопрос, какой должна быть цена актива. Однако она получила такое название, потому что позволяет определить ставку дисконтирования, используемую для расчета стоимости финансового инструмента. В модели устанавливаются следующие ограничения:
● рынок является конкурентным;
● активы ликвидны и делимы;
● отсутствуют налоги, транзакционные издержки, банкротства;
● все инвесторы имеют одинаковые ожидания, действуют рационально, стремясь максимизировать свою полезность, имеют возможность брать кредит и предоставлять средства под ставку без риска;
● рассматривается один временной период;
● доходность является только функцией риска;
● изменения цен активов не зависят от существовавших в прошлом уровней цен.
Рассмотрим, прежде всего, линию рынка капитала.
20.1.1. Линия рынка капитала (CML)
В САРМ зависимость между риском и ожидаемой доходностью можно описать с помощью линии рынка капитала (CML – Capital Market Line), которая представлена на рис. 20.1.
На графике М – это рыночный портфель, rf – актив без риска с доходностью rf ; rf L – линия рынка капитала; σm – ожидаемый риск рыночного портфеля; E(rm) – ожидаемая доходность рыночного портфеля.
Все возможные оптимальные (эффективные) портфели, т. е. портфели, которые включают в себя рыночный портфель М, расположены на линии rf L. Она проходит через две точки – rf и М. Таким образом, линия рынка капитала является касательной к эффективной границе Марковица и представляет собой не что иное как эффективную границу портфелей при возможности заимствования и кредитования. CML получила такое название именно потому, что составляющие ее портфели формируют, заимствуя средства или предоставляя кредиты под ставку без риска на рынке капитала.
Все другие портфели, в которые не выходит рыночный портфель, располагаются ниже линии rf L. CML поднимается вверх слева направо и говорит о том, что, если портфель имеет более высокий риск, он должен иметь и более высокую ожидаемую доходность.
Соответственно, если вкладчик желает получить более высокую ожидаемую доходность, он должен согласиться на более высокий риск. Наклон CML следует рассматривать как вознаграждение в единицах ожидаемой доходности за каждую дополнительную единицу риска, которую берет на себя вкладчик.
Когда вкладчик приобретает актив без риска, он обеспечивает себе доходность на уровне ставки без риска rf. Если он стремится получить более высокую ожидаемую доходность, то он должен согласиться на некоторый риск.
Ставка без риска ( rf ) является вознаграждением за время, т. е. деньги во времени имеют ценность. Дополнительная доходность, получаемая инвестором сверх ставки без риска, есть вознаграждение за риск.
Таким образом, вознаграждение лица, инвестировавшего свои средства в рыночный портфель, складывается из ставки rf, которая является вознаграждением за время, вознаграждения за риск в размере E(rm) – rf. Другими словами, на финансовом рынке его участники уторговывают между собой цену времени и цену риска.
CML представляет собой прямую линию. Уравнение прямой можно представить следующим образом:
где а – значение ординаты в точке пересечения её с линией CML, оно соответствует ставке без риска rf:
Угол наклона определяется как отношение изменения значения функции к изменению аргумента. В нашем случае (рис. 20.1) угол наклона равен:
Поскольку ожидаемая доходность (у) есть функция риска (х) , то в уже принятых терминах доходности и риска уравнение CML примет вид:
где σi – риск i-го портфеля, для которого определяется уровень ожидаемой доходности;
E(ri) – ожидаемая доходность i-го портфеля.
Данное уравнение можно записать следующим образом:
(20.1)
Таким образом, ожидаемая доходность портфеля равнее ставке без риска плюс произведение отношения риска портфеля к риску рыночного портфеля и ставкой без риска.
Пример 20.1. Ставка без риска равна 10%, ожидаемая доходность рыночного портфеля 25%, риск рыночного портфеля 15%. Определить ожидаемую доходность портфеля, риск которого составляет 30%.
Решение. Ожидаемая доходность равна:
Как мы отметили выше, наклон CML следует рассматривать как вознаграждение инвестора за риск в условиях равновесия на рынке. Поэтому он является рыночной ценой риска. Таким образом, рыночная цена риска (b) равна:
CML говорит о соотношении риска и ожидаемой доходности только для широко диверсифицированных портфелей, т. е. портфелей, включающих рыночный портфель. Но CML не отвечает на вопрос, какой ожидаемой доходностью должны обладать менее диверсифицированные портфели или отдельные активы.
20.1.2. Рыночный и нерыночный риски. Эффект диверсификации
Риск, с которым связано владение активом, можно разделить на две части.
Первая составляющая – это рыночный риск. Его также именуют не диверсифицированным, или не специфическим, или системным. Он связан с динамикой экономического цикла, общезначимыми событиями, например, войной, революцией. Когда экономика находится на подъеме, подавляющее большинство активов будет приносить более высокую доходность. Если наблюдается спад, то падает и доходность финансовых инструментов. Данный риск нельзя исключить, так как этой риск всей системы.
Вторая часть – нерыночный риск, или специфический, или диверсифицированный риск. Он связан с индивидуальными особенностями конкретного актива, а не с состоянием рынка в целом. Например, владелец акции подвергается риску потерь в связи с забастовкой на данном предприятии, некомпетентностью его руководства и т. п. Данный риск является диверсифицируемым, поскольку его можно свести практически к нулю с помощью диверсификации портфеля.
Как показали исследования западных ученых, анализировавших динамику доходности акций во второй половине 1960-х – начале 1970-х годов, портфель, состоявший из 20 активов, способен был фактически полностью исключить нерыночный риск. В случае международной диверсификации количество акций могло быть ограничено десятью. Исследования, проведенные в начале XXI века, говорят о том, что по сравнению с ми годами в 1980-е – 1990-е годы корреляция между акциями уменьшилась и возросла их волатильность, связанная с нерыночным риском. Это требует сейчас более широкой диверсификации портфеля по составу акций для достижения того же уровня риска, что и в е годы.
Широко диверсифицированный портфель заключает в себе практически только рыночный риск. Слабо диверсифицированный портфель обладает как рыночным, так и нерыночным риском. Таким образом, инвестор может снизить свой риск только до уровня рыночного, если сформирует широко диверсифицированный портфель.
Приобретая актив, вкладчик рассчитывает получить компенсацию за риск, на который он идет. Каким образом рынок будет компоненты риска с точки зрения ожидаемой доходности?
Как было сказано выше, инвестор способен практически полностью исключить специфический риск за счет формирования широко диверсифицированного портфеля. В рамках модели САРМ предполагается, что вкладчик может свободно покупать и продавать активы без дополнительных издержек. Поэтому формирование более диверсифицированного портфеля не ведет к увеличению его расходов. Таким образом, без затрат вкладчик может легко исключить специфический риск. Поэтому в теории полагается, что нерыночный риск не подлежит вознаграждению, поскольку его легко можно устранить за счет диверсификации. В связи с этим, если инвестор не диверсифицирует должным образом свой портфель, он идет на ненужный риск с точки зрения той выгоды, которую он приносит обществу.
Приобретая, например, акцию, инвестор финансирует производство и таким образом приносит обществу пользу. Покупка акции связана с рыночным риском, который является неустранимым. Поэтому инвестор должен получать вознаграждение адекватное только данному риску. В противном случае он не приобретет эту бумагу, и экономика не получит необходимые финансовые ресурсы. Однако общество (рынок) не будет вознаграждать его за специфический (не рыночный) риск, поскольку он легко устраняется диверсификацией. С точки зрения финансирования потребностей экономики данный риск не имеет смысла. Таким образом, вознаграждению подлежит только систематический (рыночный) риск. Поэтому стоимость активов должна оцениваться только относительно величины именно этого риска.
Весь риск актива (портфеля) измеряется такими показателями как дисперсия и стандартное отклонение. Для оценки рыночного риска служит другая величина, которую называют бета.
Воздействие диверсификации на риск портфеля. Как отмечалось выше, на риск портфеля основное влияние оказывает степень корреляции доходностей входящих в портфель акций – чем ниже уровень корреляции, т. е. чем ближе коэффициент корреляции приближается к (-1), тем ниже риск портфеля. Тогда можно предположить, что путем диверсификации – изменения количества входящих в портфель ценных бумаг и их характеристик – инвестор способен снизить уровень риска портфеля, не изменяя при этом его ожидаемой доходности.
Диверсификация, как процесс изменения содержимого портфеля, должна приниматься с учетом того, что варианты формирования портфеля бесконечно повторяются. Только с этим допущением можно добиться основного предназначения диверсификации – снижения риска без существенного снижения ожидаемой доходности формируемого портфеля. Действительно, если понимать диверсификацию как процесс формирования всех возможных вариантов портфелей, то мы должны прийти к выводу, что ожидаемая доходность портфеля любого объема должна в конечном итоге стремиться к ожидаемой доходности рыночного портфеля.
Чтобы доказать справедливость подобного утверждения, положим для простоты, что имеются три ценные бумаги со следующими характеристиками:
Источник